11. Присоединённая задача на минимум. Уравнение Якоби
Построим для задачи (2) уравнение Эйлера:
(4)
Это уравнение называется уравнением Якоби вдоль допустимой кривой у.
(4*)
Подсчитаем
коэффициенты
:
.
12. Условие Лежандра-Клебша
Т. Пусть
– слабая минималь ОЗВИ, тогда
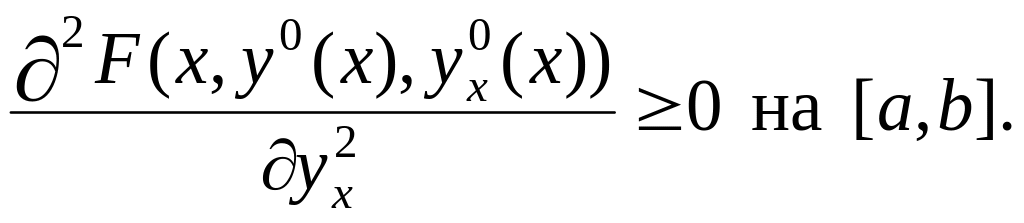
Доказательство.
Пусть
– слабая минималь. Предположим противное:
.
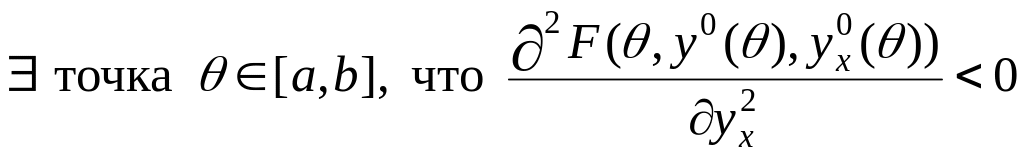Поскольку
непрерывная функция, то можно считать,
что точка
-внутренняя
и
такое малое
,
что будет выполняться:
(5)
Построим тогда
функцию
следующим образом:
,
тогда производная
Ч.т.д.
13. Условие Якоби
О.
Пусть
некоторая зафиксированная допустимая
кривая. Составим для неё присоединённую
задачу на минимум, построим уравнение
Якоби, найдём общее решение:
.
Исключаем одну из производных постоянных
с помощью условия
,
тогда получим семейство решений:
.
Если для некоторого с
и для некоторой точки
,
выполняется условие:
,
то говорят, что точка
сопряжена с
точкой а, вдоль допустимой кривой у.
Иначе говоря, сопряжена с точкой а, если такое нетривиальное решение уравнения Якоби , что выполняется условие:
где
– решение уравнения Якоби (одно из них).
Точки
сопряжены с точкой а.
Т.
Пусть
– неособая слабая минималь ОЗВИ (то
есть
),
тогда вдоль неё не существует точек
сопряжённых с точкой
.
14. Достаточное условие слабого минимума
О. Пусть
– допустимая кривая. Говорят, что она
удовлетворяет
усиленному
условию Лежандра,
если она удовлетворяет условию:
.
Допустимая кривая
удовлетворяет
усиленному
условию Якоби,
если вдоль неё не существует точек
сопряжённых с a,
где
Т. Пусть – допустимая кривая и пусть она:
1 является экстремалью,
2 удовлетворяет усиленному условию Лежандра,
3 удовлетворяет усиленному условию Якоби.
Тогда – слабая минималь основной задачи.
15. Простейшая задача терминального управления (пзту)
Пусть имеется
некоторый объект, поведение которого
изменяется во времени на [
]
(
– начальный момент уравнения,
– конечный) и описывает вектор М:
– фазовые координаты объекта
Пусть объект – это ракета, которая запускается на орбиту земли.
Предположим, что
вектор x(t)
удовлетворяет дифференциальному
уравнению:
(1)
с начальным
условиями:
(2),где
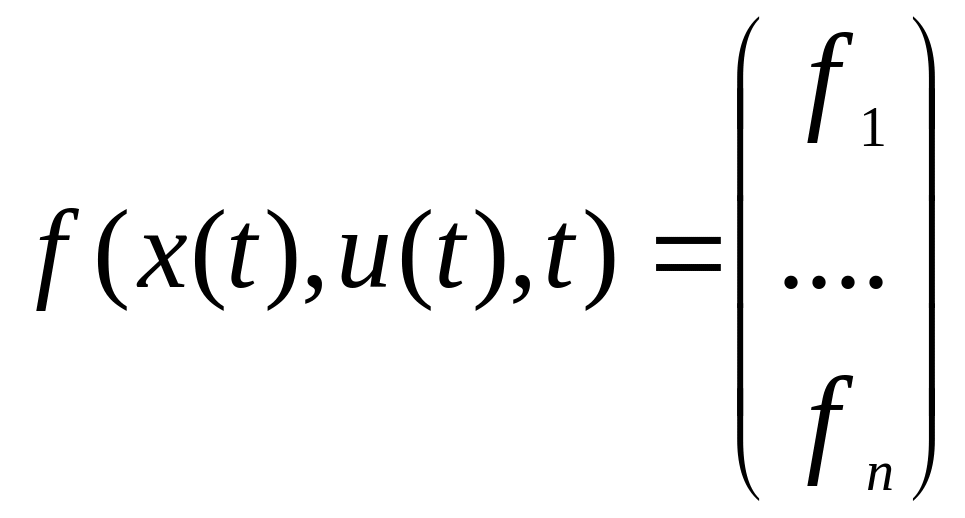– функция трёх переменных.
– вектор управляющих
воздействий,
– начальное положение объекта.
Относительно функции f и u будем считать их такими, что при выборе управления u решение задачи Коши (1)-(2) будет существовать и при чём единственным образом и будем говорить, что управление u(t) будет порождать траекторию x(t).
О. Говорят, что некоторая функция u(t), будет являться допустимым управлением, если:
1
– кусочно-непрерывная
функция (функциональном ограничении),
2
,
где U
– некоторый компакт (замкнутое,
ограниченное множество),
(это геометрическое ограничение).
Множество всех
дифференциальных уравнений будем
обозначать
Введём функционал
качества управления: положим
(3)
где φ(х)
– скалярная функция в
(каждому
вектору из
ставит в соответствие некоторое число).
Функционал (3) называется терминальным функционалом, так как он задан на конце траектории объекта. Он неявно зависит от допустимого управления, а через задачу (1)-(2), а именно:
если возьмём
некоторое дифференциальное уравнение
,
подставим его в задачу (1)-(2), решив задачу,
получим:
затем определим вектор
– конечное положение и затем вычислим
число
,
то это и будет цена управления (стоимость).
Простейшая задача терминального управления:
(4)