
- •Теорема сложения вероятностей
- •Условная вероятность Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
- •Независимые события
- •Дискретные случайные величины
- •Примеры дискретных случайных величин:
- •2) Дискретная биномиальная случайная величина(биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом:
- •3) Дискретная случайная величина Пуассона(пуассоновское распределение с параметром ). Закон распределения дискретной случайной величины Пуассона задается следующим образом:
- •4) Дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид
- •Непрерывные случайные величины
- •Примеры непрерывных случайных величин:
- •3) Равномерная на [a;b] непрерывная случайная величина(равномерное на отрезке [a;b] распределение).
- •Биномиальное распределение
- •Распределение Пуассона
- •Простейшие свойства математического ожидания
- •[Править]Тождества
- •Описание
- •Характеристики
- •Графическое изображение рядов распределения
- •Полигон
- •6.1. Распределение домохозяйств по размеру
- •Статистическая таблица
- •Гистограмма
- •8.1 Определения и основные свойства точечных оценок
- •8.3. Метод максимального правдоподобия
- •3. Интервальные оценки
Независимые события
Будем
считать, что дано фиксированное вероятностное
пространство ![]() .
.
Определение
1. Два
события ![]() независимы,
если
независимы,
если
Вероятность появления события A не меняет вероятности события B.
Замечание
1. В
том случае, если вероятность одного
события, скажем ![]() ,
ненулевая, то есть
,
ненулевая, то есть ![]() ,
определение независимости эквивалентно:
,
определение независимости эквивалентно:
![]()
то
есть условная
вероятность события ![]() при
условии
равна
безусловной вероятности события
.
при
условии
равна
безусловной вероятности события
.
Определение
2. Пусть
есть семейство (конечное или бесконечное)
случайных событий ![]() ,
где
,
где ![]() —
произвольное индексное множество. Тогда
эти события попарно
независимы,
если любые два события из этого семейства
независимы, то есть
—
произвольное индексное множество. Тогда
эти события попарно
независимы,
если любые два события из этого семейства
независимы, то есть
![]()
Определение
3. Пусть
есть семейство (конечное или бесконечное)
случайных событий
.
Тогда эти события совместно
независимы,
если для любого конечного набора этих
событий ![]() верно:
верно:
![]()
Замечание 2. Совместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно.
Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:
 :
монеты 1 и 2 упали одной и той же стороной;
:
монеты 1 и 2 упали одной и той же стороной;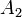 :
монеты 2 и 3 упали одной и той же стороной;
:
монеты 2 и 3 упали одной и той же стороной;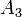 :
монеты 1 и 3 упали одной и той же стороной;
:
монеты 1 и 3 упали одной и той же стороной;
Легко
проверить, что любые два события из
этого набора независимы. Все же три в
совокупности зависимы, ибо зная, например,
что события ![]() произошли,
мы знаем точно, что
также
произошло.
произошли,
мы знаем точно, что
также
произошло.
11.Формула полной вероятности
Пусть событие В может наступать только при условии появления одного из событий Аi, образующих полную систему событий. Тогда вероятнсть события В равна сумме произведений вероятностей каждого из событий Аi на соответствующую условную вероятность события А:
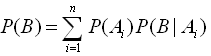
Эта формула носит название формулы полной вероятности.
12.Формула Байеса
Если вероятности событий до опыта были Р(А), то с учетом появления в результате опыта события В условная вероятность Р(A|B) вычисляется по формуле Байеса:
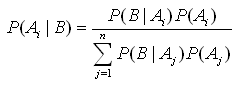
13.формула Бернулли
Формулировка
Теорема: Если
Вероятность p наступления
события Α в
каждом испытании постоянна, то
вероятность ![]() того,
что событие A наступит k раз
в n независимых
испытаниях, равна:
того,
что событие A наступит k раз
в n независимых
испытаниях, равна: ![]() ,
где
,
где ![]() .
.
[править]Доказательство
Так
как в результате ![]() независимых
испытаний, проведенных в одинаковых
условиях, событие
наступает
с вероятностью
независимых
испытаний, проведенных в одинаковых
условиях, событие
наступает
с вероятностью ![]() ,
следовательно противоположное ему
событие с вероятностью
,
следовательно противоположное ему
событие с вероятностью ![]() .
.
Обозначим ![]() —
наступление события
в
испытании с номером
—
наступление события
в
испытании с номером ![]() .
Так как условия проведения опытов
одинаковые, то эти вероятности равны.
Пусть в результате
опытов
событие
наступает
.
Так как условия проведения опытов
одинаковые, то эти вероятности равны.
Пусть в результате
опытов
событие
наступает ![]() раз,
тогда остальные
раз,
тогда остальные ![]() раз
это событие не наступает. Событие
может
появиться
раз
в
испытаниях
в различных комбинациях, число которых
равно количеству
сочетаний из
элементов
по
.
Это количество сочетаний находится по
формуле:
раз
это событие не наступает. Событие
может
появиться
раз
в
испытаниях
в различных комбинациях, число которых
равно количеству
сочетаний из
элементов
по
.
Это количество сочетаний находится по
формуле:
![]() .
.
При этом вероятность каждой комбинации равна произведению вероятностей:
![]() .
.
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:
, где .
14.локальная теорема Лапласа.
Локальная теорема Лапласа
![]()
![]()
![]()
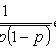
![]()
где ![]()
![]() -
вероятность появления события A ровно k раз
при n независимых
испытаниях; p -
вероятность появления события A при
каждом испытании;
-
вероятность появления события A ровно k раз
при n независимых
испытаниях; p -
вероятность появления события A при
каждом испытании; ![]()
![]()
![]()
![]() .
.
15.интегральная теорема Лапласа
Интегральная теорема Лапласа
![]()
![]()
![]()
![]()
![]()
где ![]()
![]() -
вероятность того, что в n независимых
испытаниях событие A появится
не менее k1 и
не более k2 раз;
-
вероятность того, что в n независимых
испытаниях событие A появится
не менее k1 и
не более k2 раз; ![]()
![]()
![]()
![]()
![]() -
функция Лапласа;
-
функция Лапласа; ![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
![]()
![]() .
.
Оценка отклонения относительной частоты от постоянной вероятности
![]()
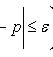
![]()
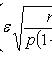
![]()
![]()
![]()
![]()
![]()
Наивероятнейшее число k0 появления события A при n независимых испытаниях
![]()
![]()
![]()
![]()
![]()
(n - число испытаний; p - вероятность появления события при одном испытании).
16.дискретные и непрерывные случайные величины
Одним из основных в теории вероятностей является понятие случайной величины. Случайная величина - это величина, принимающая те или иные значения в зависимости от случая. Примерами случайных величин могут быть: число выпавших очков, при подбрасывании игральной кости; число попаданий в цель при k выстрелах и т.д. Множества всех случайных величин в зависимости от типа их распределения делится на три класса: дискретные случайные величины, непрерывные случайные величины исингулярные случайные величины. В этой статье мы рассмотрим первые два класса:дискретные случайные величины и непрерывные случайные величины.
