Билет №10

1. Закон сохранения импульса. Реактивное движение.

2. Энергия плоского конденсатора. Энергия электрического поля.

1. Закон сохранения импульса утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

F2=-F1

F2t=-F1t

F1t=mV1’-mV1

F2t=mV2’-mV2

mV2’-mV2= -(mV1’-mV1)

mV2’-mV2= -mV1’+mV1

mV1+mV2 = mV1’+mV2’

Реактивное движение - движение тела, обусловленное отделением от него с некоторой скоростью какой-то его части. Реактивное движение описывается, исходя из закона сохранения импульса

2. Заряженный конденсатор обладает энергией. Получим выражение для этой энергии, рассматривая плоский конденсатор. Пусть одна из пластин заряженного конденсатора перемещается к другой под действием кулоновских сил до полного соприкосновения. При соприкосновении заряд становится равным нулю, конденсатор исчезает, а это означает, что становится равной нулю и энергия конденсатора. Следовательно, работа действовавшей на пластину электрической силы равна энергии, первоначально запасенной в конденсаторе. Найдем эту работу. Сила, действующая на движущуюся пластину, равна произведению ее заряда на напряженность поля, созданного другой пластиной. Напряженность однородного электрического поля, создаваемого пластиной конденсатора, равна Е = 2pks, где s – поверхностная плотность заряда на пластине . И, следовательно, искомая работа равна .

Таким образом, выражение для энергии конденсатора имеет вид:

Поскольку заряд конденсатора и напряжение на нем связан соотношением , то для энергии заряженного конденсатора можно записать и другие выражения:

Энергию заряженного конденсатора можно выразить и через напряженность поля внутри конденсатора. Так как напряжение между обкладками конденсатора , а емкость конденсатора , то для энергии конденсатора:

где V – объем электрического поля между обкладками конденсатора. Так как энергия конденсатора пропорциональна его объему, то величина:

является объемной плотностью энергии электрического поля.

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:

Билет №11

1.Гидростатическое давление. Закон Паскаля. Гидравлический пресс.

2. Распределение Максвелла.

1.Давление(p): p = F/S.

Закон Паскаля - закон гидростатики, согласно которому давление на поверхность жидкости, произведённое внешними силами, передаётся жидкостью одинаково во всех направления.

p1 = p2 = p3

Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg, где m = ρhS – масса жидкости в сосуде, ρ – плотность жидкости. Следовательно

p = F/S = mg/S = ρhSg/S = ρgh.

Давление столба жидкости ρgh называют гидростатическим давлением.

Таким образом, полное давление в жидкости на глубине h можно записать в виде: p = p0+ρgh.

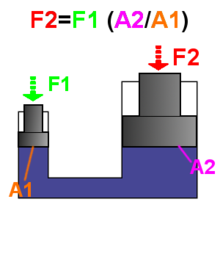
Гидравлический пресс — это промышленная машина, которая позволяет, прилагая в одном месте небольшое усилие, одновременно получать в другом месте высокое усилие. Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью водой, маслом или другой подходящей жидкостью.

2.МА́КСВЕЛЛА РАСПРЕДЕЛЕ́НИЕ, распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, (в отсутствии внешнего поля, при условии, что движение частиц подчиняется законам классической механики. Установлено Дж. К. Максвеллом в 1859.

Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля.

Функция распределения молекул по скоростям f(v)=dN(v)/Ndv определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv и имеет смысл плотности вероятности.

Для газа, подчиняющегося классической механике, в состоянии статистического равновесия функция распределения f Максвелла по скоростям имеет вид:

f(v) =n(m/2pkT)^3/2exp(-mv²/2kT),

Где m — масса молекулы, Т — абсолютная температура системы, k — постоянная Больцмана.

Значение функции распределения f(v) зависит от рода газа (от массы молекул) и от температуры.

С помощью распределения Максвелла можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скорость

v² = 3kT/m, а средняя скорость молекулы v = (8kT/pm)^1/2.

Распределение Максвелла не зависит от взаимодействия между молекулами и справедливо не только для газов, но и для жидкостей, если для них возможно применить классическое описание.

Распределение Максвелла вытекает из Гиббса распределения канонического в том случае, когда поступательное движение частиц можно рассматривать в классическом приближении, учитывая, что распределение по скоростям не зависит от распределения по пространственным координатам. Распределение Максвелла является частным решением кинетического уравнения Больцмана для случая статистического равновесия в отсутствии внешних полей. Распределение Максвелла не зависит от характера взаимодействия частиц системы и от внешних сил и потому справедливо как для молекул газа, так и для молекул жидкостей и твердых тел. Распределение Максвелла справедливо также для случая броуновского движения частиц, взвешенных в газе или жидкости.