7. Индексные системы за ряд последовательных периодов.

Часто в ходе экономического анализа изменение индексируемых величин изучают не за два, а за ряд последовательных периодов. Следовательно, возникает необходимость построения индексов за ряд этих последовательных периодов, которые образуют индексные системы. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.

В зависимости от базы сравнения индексы бывают цепными и базисными.

В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.

7. Индексы постоянного и переменного состава.

Индексный метод широко применяется для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.  Индекс переменного состава Iпер представляет собой отношение двух взвешенных средних величин, характеризующее изменение индексируемого (осредняемого) показателя.

Величина этого индекса характеризует изменение средней взвешенной за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.  Индекс постоянного (фиксированного) состава Iфикс представляет собой отношение средних взвешенных с одними и теми же весами (т.е. при постоянной структуре).

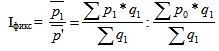
Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.  Индекс структурных сдвигов Iстр характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя.

Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности к общей их численности.  Система взаимосвязанных индексов при анализе динамики средних величин имеет вид:

Доля отдельной группы: 

   

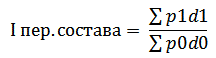
I пост.соства тождественен сводному агрегатному индексу цен Ip  Абсолютное изменение среднего уровня качественного показателя под влиянием каждого фактора в отдельности, а также их совместного изменения,определяется как разность делимого и делителя по соответствующему индексу

7. Территориальные (пространственные) индексы.

Территориальные индексы представляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления.

Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения т.е.

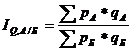
Различие объемов товарооборота вызвано различием ассорти­мента и количества проданных товаров, а также цен.

Терри­ториальный индекс физического объема товарооборота рас­считывается по следующей формуле:

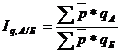
где р — средняя межрайонная цена товара каждого вида,

 

Территориальный индекс цен определяется:

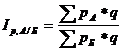
где q - суммарный по двум районам объем продаж каждого вида товара.

Такие сложные взвешивающие показатели применяются для того, чтобы результаты расчета были обратимыми, т. е. чтобы выполнялись соотношения:

      и       

Условия индексной модели могут нарушаться, хотя и не очень существенно. Использование таких территориальных индексов для анализа абсолютной разницы товарооборотов дает в только приближенный результат.

Территориальные индексы можно также рассчитывать:

• с использованием соизмерителей только района А или только района Б;

• как среднюю геометрическую из двух территориальных индексов, рассчитанных с разными территориальными весами.