
- •Решение.
- •4) Найдем основные числовые характеристики вариационного ряда:
- •Задача 2.
- •Решение.
- •Задание на самостоятельную работу.
- •Номер варианта соответствует порядковому номеру студента в списке группы.
- •Исходные данные к заданию 1
- •Исходные данные к заданию 2
- •Численность работников органов местного самоуправления в ряде регионов России в 2008 г. (тыс. Человек)
- •Среднемесячная заработная плата работников органов местного самоуправления в ряде регионов России в 2008 г. (тыс. Руб.)
- •Численность населения в ряде регионов России на конец 2008 г. (тыс. Человек)
- •Удельный вес городского населения в ряде регионов России в 2008 г. (%)
- •Удельный вес сельского населения в ряде регионов России в 2008 г. (%)
- •Доля населения моложе трудоспособного возраста в ряде регионов России в 2008г. (%)
- •Доля населения в трудоспособном возрасте в ряде регионов России в 2008 г. (%)
- •Доля населения старше трудоспособного возраста в ряде регионов России в 2008 г. (%)
- •Коэффициент демографической нагрузки в ряде регионов России в 2008 г. (чел)
- •Число родившихся на 1000 человек населения в ряде регионов России в 2008 г. (чел)
- •Число умерших на 1000 человек населения в ряде регионов России в 2008 г. (чел)
- •Число разводов на 1000 браков в ряде регионов России в 2008 г.
- •Численность экономически активного населения в ряде регионов России в 2008 г. (тыс. Человек)
- •Среднегодовая численность занятых в экономике в ряде регионов России в 2008 г. (тыс. Человек)
- •Численность занятых в отрасли «Образование» в ряде регионов России в 2008 г. (тыс. Человек)
- •Численность занятых в отрасли «Здравоохранение и предоставление социальных услуг» в ряде регионов России в 2008 г. (тыс. Человек)
- •Численность безработных в ряде регионов России в 2008 г. (тыс. Человек)
- •Численность работников государственных органов и органов местного самоуправления в ряде регионов России в 2008 г. (тыс. Человек)
- •Численность пенсионеров в ряде регионов России в 2008 г. (тыс. Человек)
- •Доля пенсионных выплат в общем объеме социальных выплат в ряде регионов России в 2008 г. (%)
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА И ГОСУДАРСТВЕННОЙ СЛУЖБЫ при ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОРЛОВСКИЙ ФИЛИАЛ
кафедра математики и математических методов в управлении
Самостоятельная работа
по математике
на тему «Вариационный ряд и его характеристики»
для студентов очного отделения факультета «Экономика и менеджмент»
направления подготовки «Управление персоналом»
Орел, 2012
Цель работы: Освоение понятий математической статистики и приемов первичной обработки данных.
Пример решения типовых задач.
Задача 1.
Путем опроса
получены следующие данные (![]() ):
):
1 2 3 2 2 4 3 3 5 1 0 2 4 3 2 2 3 3 1 3 2 4 2 4 3 3 3 2 0 6
3 3 1 1 2 3 1 4 3 1 7 4 3 4 2 3 2 3 3 1 4 3 1 4 5 3 4 2 4 5
3 6 4 1 3 2 4 1 3 1 0 0 4 6 4 7 4 1 3 5
Необходимо:
1) Составить вариационный ряд (статистическое распределение выборки), предварительно записав ранжированный дискретный ряд вариантов.
2) Построить полигон частот и кумуляту.
3) Составить ряд распределения относительных частот (частостей).
4) Найти основные
числовые характеристики вариационного
ряда (использовать упрощенные формулы
для их нахождения): а) среднюю арифметическую
![]() ,
б) медиану Ме
и моду Мо,
в) дисперсию s2,
г) среднее квадратическое отклонение
s,
д) коэффициент вариации V.
,
б) медиану Ме
и моду Мо,
в) дисперсию s2,
г) среднее квадратическое отклонение
s,
д) коэффициент вариации V.
5) Пояснить смысл полученных результатов.
Решение.
1) Для составления ранжированного дискретного ряда вариантов отсортируем данные опроса по величине и расположим их в порядке возрастания
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
5 5 5 5 6 6 6 7 7.
Составим вариационный ряд, записав в первую строку таблицы наблюдаемые значения (варианты), а во вторую соответствующие им частоты (таблица 1)
Таблица 1.
Варианты xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
∑ |
Частота ni |
4 |
13 |
14 |
24 |
16 |
4 |
3 |
2 |
80 |
Накопленная частота niнак |
4 |
17 |
31 |
55 |
71 |
75 |
78 |
80 |
- |
2) Полигон частот представляет собой ломаную, соединяющую точки (хi; ni), i=1, 2,…, m, где m – число различных значений признака X.
Изобразим полигон частот вариационного ряда (рис. 1).
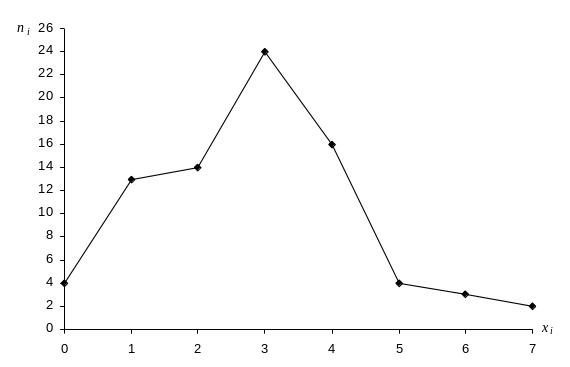
Рис.1. Полигон частот
Кумулятивная кривая (кумулята) для дискретного вариационного ряда представляет ломаную, соединяющую точки (хi; niнак), i=1, 2,…, m.
Найдем накопленные частоты niнак (накопленная частота показывает, сколько наблюдалось вариантов со значением признака меньшим х). Найденные значения заносим в третью строку таблицы 1.
Построим кумуляту (рис. 2).
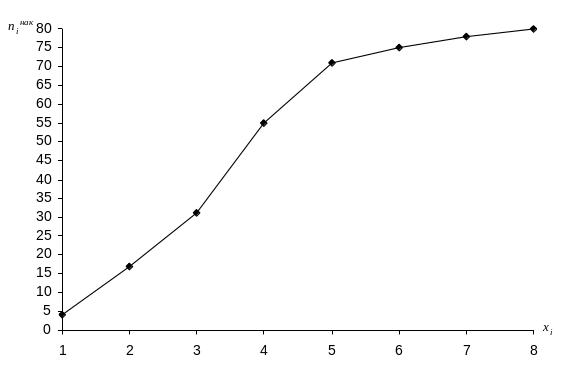
Рис.2. Кумулята
3)
Найдем относительные частоты (частости)
![]() ,
где
,
где
![]() ,
где m
– число различных значений признака
X,
которые будем вычислять с одинаковой
точностью.
,
где m
– число различных значений признака
X,
которые будем вычислять с одинаковой
точностью.
Запишем ряд распределения относительных частот (частостей) в виде таблицы 2
Таблица 2
Варианты xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
∑ |
Частость wi |
0,0500 |
0,1625 |
0,1750 |
0,3000 |
0,2000 |
0,0500 |
0,0375 |
0,0250 |
1 |
Накопленная частость wiнак |
0,0500 |
0,2125 |
0,3875 |
0,6875 |
0,8875 |
0,9375 |
0,9750 |
1,0000 |
|
4) Найдем основные числовые характеристики вариационного ряда:
а) Среднюю арифметическую найдем, используя упрощенную формулу:
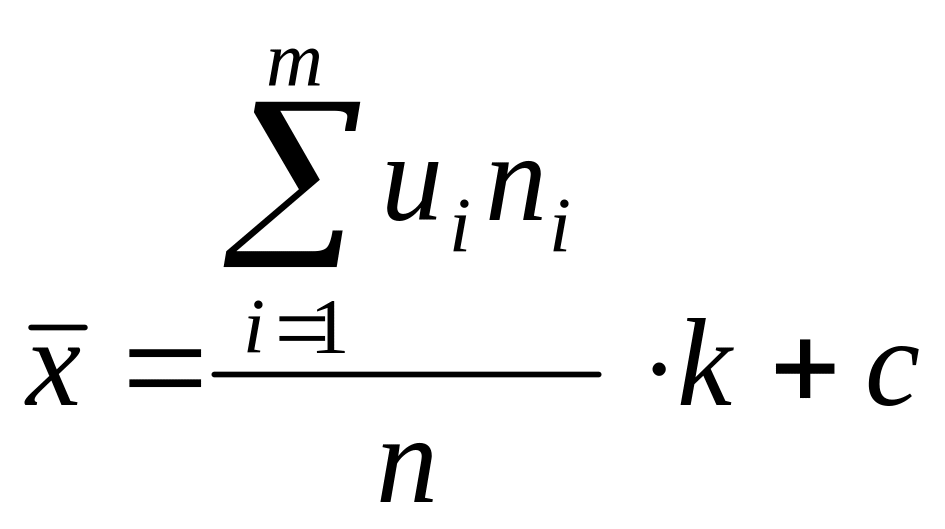 ,
,
где
![]() - условные варианты
- условные варианты
Положим с = 3 (одно из средних наблюдаемых значений), k = 1 (разность между двумя соседними вариантами) и составим расчетную таблицу (табл. 3).
Таблица 3.
xi |
ni |
ui |
ui ni |
ui2 ni |
0 |
4 |
-3 |
-12 |
36 |
1 |
13 |
-2 |
-26 |
52 |
2 |
14 |
-1 |
-14 |
14 |
3 |
24 |
0 |
0 |
0 |
4 |
16 |
1 |
16 |
16 |
5 |
4 |
2 |
8 |
16 |
6 |
3 |
3 |
9 |
27 |
7 |
2 |
4 |
8 |
32 |
Сумма |
80 |
|
-11 |
193 |
Тогда средняя арифметическая

б) Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений. Данный дискретный вариационный ряд содержит четное число членов (n=80), значит, медиана равна полусумме двух серединных вариантов.
![]()
Модой Мо вариационного ряда называется вариант, которому соответствует наибольшая частота. Для данного вариационного ряда наибольшая частота nmax = 24 соответствует варианту х = 3, значит мода Мо=3.
в) Дисперсию s2, которая является мерой рассеяния возможных значений показателя X вокруг своего среднего значения, найдем, используя упрощенную формулу:
 ,
где ui
– условные варианты
,
где ui
– условные варианты
Промежуточные вычисления также занесем в таблицу 3.
Тогда дисперсия

г) Среднее квадратическое отклонение s найдем по формуле:
![]()
![]() .
.
д) Коэффициент
вариации V:
![]() (
(![]() ),
),
Коэффициент вариации является безмерной величиной, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность.
Коэффициент вариации
![]() .
.
5)
Смысл полученных результатов заключается
в том, что величина
![]() характеризует среднее значение признака
X
в пределах рассматриваемой выборки, то
есть среднее значение составило 2,86.
Среднее квадратическое отклонение s
описывает абсолютный разброс значений
показателя X
и в данном случае составляет s
≈ 1,55. Коэффициент вариации V
характеризует относительную изменчивость
показателя X,
то есть относительный разброс вокруг
его среднего значения
характеризует среднее значение признака
X
в пределах рассматриваемой выборки, то
есть среднее значение составило 2,86.
Среднее квадратическое отклонение s
описывает абсолютный разброс значений
показателя X
и в данном случае составляет s
≈ 1,55. Коэффициент вариации V
характеризует относительную изменчивость
показателя X,
то есть относительный разброс вокруг
его среднего значения
![]() ,
и в данном случае составляет
,
и в данном случае составляет
![]() .
.
Ответ:
;
![]() ;
;
![]() ;
.
;
.
