
- •Для специальностей
- •2. Сумма и произведение событий.
- •3. Формулы полной вероятности и Байеса.
- •4. Приближенные вычисления в схеме Бернулли. Локальная и интегральная теоремы Лапласа.
- •Ответ: р400(300,330)≈0,8882. Контрольные вопросы
- •Методические указания к выполнению самостоятельной работы
- •Исходные данные к расчетному заданию 1
- •Исходные данные к расчетным заданиям 2 и 3
- •Сходные данные к расчетным заданиям 4 и 5
РОССИЙСКАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ
ОРЛОВСКАЯ РЕГИОНАЛЬНАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ
КАФЕДРА МАТЕМАТИКИ И МАТЕМАТИЧЕСКИХ МЕТОДОВ В УПРАВЛЕНИИ
Самостоятельная работа по математике
Тема: «Действия над событиями»
Для специальностей
«Экономика»
«Экономическая безопасность»
Составил: доцент Афонина Т.Н.
Рекомендовано кафедрой: «Математики и математических методов в управлении»
Зав. кафедрой, доктор эконом. наук, профессор
___________________________Шуметов В.Г.
ОРЕЛ 2009
Цели и задачи самостоятельной работы:
Закрепление знаний, полученных на лекциях по теории вероятности, путем решения типовых задач. Усвоение понятий основных видов случайных событий и отработка навыков алгебраических действий над событиями.
Основные положения теории вероятностей изложены в учебниках:
[1] Н.Ш.Кремер Теория вероятностей и математическая статистика. - М. ЮНИТИ, 2002.
[2] М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложения в экономическом образовании. —М., «Дело», 2003.
[3] В.Е. Гмурман. Теория вероятностей и математическая статистика. - М. Высшая школа, 2000.
Самостоятельная работа "Действия над событиями" включает в себя 5 типовых задач, исходные данные для которых задаются для каждого варианта индивидуально. Варианты задаются преподавателем.
Классическое определение вероятности.
Задача 1. Получателями социальных пособий являются три группы клиентов социальной службы. Один специалист обслуживает n1 клиента из 1-ой группы, число клиентов 2-ой группы равно n2, 3-ей группы - n3. Разовая денежная выплата предназначена m клиентам. Определить вероятность того, что среди них m1 представителя 1-ой группы, m2, и m3 – второй и третьей группы соответственно.
Решение
(для
нулевого варианта: n1
=2, n2
=3, n3
=4, m1
=2, m2
=1, m3=2).
В соответствии с классическим определением,
вероятность наступления события А
находится по формуле: Р(А)=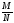 ,
где N–полное
число возможных исходов, а М–число
исходов, благоприятствующих событию
А.
В
рассматриваемой задаче полным числом
возможных исходов является количество
способов, которыми можно из всех n=
,
где N–полное
число возможных исходов, а М–число
исходов, благоприятствующих событию
А.
В
рассматриваемой задаче полным числом
возможных исходов является количество
способов, которыми можно из всех n=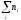 =
9 клиентов выбрать m=
=
9 клиентов выбрать m=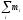 =
5 клиентов, причем, порядок выбора не
имеет значения. Число таких комбинаций
(сочетаний) находится по формуле
=
5 клиентов, причем, порядок выбора не
имеет значения. Число таких комбинаций
(сочетаний) находится по формуле
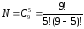 ,N=126.
,N=126.
Количество
благоприятствующих исходов находится,
как произведение числа способов выбрать
требуемое количество изделий каждого
сорта.
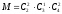 ,М=
,М=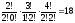
Подставляя полученные значения M и N в формулу, найдем искомую вероятность: Р = 18/126 ≈ 0,143.
Ответ: вероятность того, что из 5 наудачу выбранных клиентов окажется 2 клиента первой группы, 1 – второй и 2 – третьей группы равна 0,143.
2. Сумма и произведение событий.
Задача 2. В двух действующих банках k1 и k2 % заемщиков соответственно получают кредит для покупки нового жилья, а остальные – на приобретение потребительских товаров. Наудачу выбирают по одному заемщику из каждого банка. Какова вероятность обнаружить среди них: а) хотя бы одного получателя кредита для потребительских целей; б) двух получателей кредита на другие потребительские цели; в) одного получателя кредита для покупки нового жилья и одного заемщика средств на другие цели ?
Решение (для нулевого варианта: k1 =76, k2 =42). Введем обозначения:
р1
=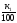 ,р2
=
,р2
=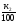 - вероятность выбрать получателей
кредита для покупки нового жилья
соответственно из первого и второго
банков;
- вероятность выбрать получателей
кредита для покупки нового жилья
соответственно из первого и второго
банков;
событие А — выбран хотя бы один получатель кредита для покупки нового жилья;
событие В — выбраны два получателя кредита на потребительские цели;
событие С — выбраны один получатель кредита для покупки нового жилья и один заемщик средств на другие цели.
а).
Найдем Р(А).
Поскольку выбор заемщиков из разных
банков – события независимые, можно
воспользоваться формулой Р(А)=
1 – Р(А),
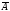 – событие, заключающееся в том, что оба
заемщика получают средства на покупку
жилья.
– событие, заключающееся в том, что оба
заемщика получают средства на покупку
жилья.

Р(А) = 1 – р1∙р2 =1-0,76∙0,42 ≈0,68.
б). Найдем Р(В). Поскольку событие В является произведением независимых событий (совместным выбором двух получателей кредита на потребительские цели), и вероятности выбора получателей потребительского кредита: q1 = 1-p1 и q2 = 1-p2,
Р(В) =(1-p1)∙(1-p2 ) = (1-0,76)∙(1-0,42) ≈ 0,14.
в). Найдем Р(С). Событие С является суммой двух несовместных событий: «один получатель кредита для покупки жилья, а второй – других продуктов потребления» и «первый – получатель потребительского кредита, а второй – получатель кредита на приобретение жилья». Каждое из этих событий является произведением соответствующих независимых событий. На основании теорем о сумме несовместных событий и произведении независимых событий можно записать: Р(С) = р1∙(1-р2) + (1-р1)∙р2.
Р(С) =0,76∙(1-0,42) + (1-0,76)∙0,42 ≈ 0,54
Ответ: Р(А) ≈ 0,68; Р(В) ≈0,14; Р(С) ≈ 0,54.
