56. Разложение функций с периодом 2l в ряд Фурье

   Пусть  g (x)  – периодическая функция с периодом 2π:   Тогда функция     является периодической с периодом 2L:   Следовательно, для разложения периодической функции  f (x)  с периодом 2L в ряд Фурье можно использовать соответствующие формулы для периодической функции с периодом 2π, выполнив в них подстановку   :

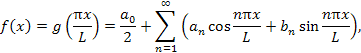
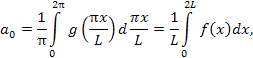
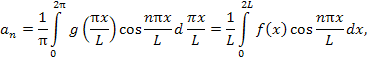
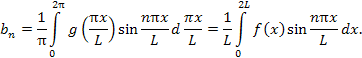
       Аналогичным образом обобщаются формулы для ряда и коэффициентов Фурье в комплексной форме на случай периодической функции  f (x)  с периодом 2L:

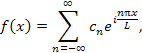
59.