10. Касательная к плоскости и нормаль к поверхности.

Если поверхность задана уравнением F(x, y, z) = 0 и точка М₀ (x₀, y₀, z₀) лежит на ней, то:Касательная плоскость к поверхности в точке М₀ определяется уравнением (х-х₀)F’_x(M₀)+(y-y₀)F’_y(M₀)+(z-z₀)F’_z(M₀) = 0.Нормаль к поверхности в точке М₀ (прямая, проходящая через точку М₀ перпендикулярно к касательной плоскости ) определяется уравнением (х-х₀)/F’_x(M₀) = (y-y₀)/F’_y(M₀) = (z-z₀)/F’_z(M₀).Точки поверхности F(x, y, z) = 0,где одновременно обращаются в 0 все частные производные первого порядка F’_x ,F’_y, F’_z называют особыми. В таких точках поверхность не имеет ни касательной плоскости, ни нормали.

11. Необходимые и достаточные условия экстремума.Необходимые условия экстремума. _, ОПР1. Ф-ция имеет локальный максимум(минимум) в если сущ-ет такая окрестность , что для М из окр-сти : если выполн усл max, если выполн обр усл то min. . 1)Если для всех дост. малых приращ. независ. пер-ной, то ф-я достигает max в 2)Если для всех дост. малых приращ. независ. пер-ной, то ф-я достигает min в Если ф-я достигает экстремума в , то частные производные первого порядка или обр в 0, или не сущ., или равны .Пусть имеет экс-мум в , то

(1)

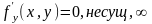
Кас. поскость параллельна при нулевых частных производных

Предположим что ф-я опр, непрерыв и имеет непрерыв частные производные 1-го и 2-го порядка опр. и не прерыв. в окрест : то в этой точке имеем экстремум, 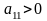min, max. Если нет экстремума. При необход исслед высшие проиводныею. Задача о наиб и наим знач ф-ции 2-х переменных в заданной обл-сти:1) Если наиб и наим знач достигается внутри этой области то оно явл экстремальным.Но если оно достигается на границе, то необход исслед на границе 3)Из эксрем. знач и значений на границе выбрать наиб и наим знач.

12. Наибольшее и наименьшие значения ( глобальные экстремумы ) функции двух переменных в замкнутой области

Пусть функция z=f(x,y) определена и непрерывна в ограниченной замкнутой области D. Тогда в области D она достигает своих наименьшего и наибольшего значений, причем эти значения достигаются либо внутри области D, либо на границе. Точки, в которых функция принимает наибольшее или наименьшее значения в ограниченной замкнутой области, называют также точками абсолютного или глобального экстремума. Если наибольшее или наименьшее значения достигаются во внутренних точках области, то это точки локального экстремума функции z=f(x,y). Таким образом, точки, в которых функция принимает наибольшее или наименьшее значения являются либо локальными экстремумами, либо граничными точками области.

Следовательно, чтобы найти наибольшее и наименьшее значения функции z=f(x,y) в ограниченной замкнутой области D, следует вычислить значение функции в критических точках области D, а также наибольшее и наименьшее значения функции на границе.

Если граница задана уравнением φ(x,y)=0, то задача отыскания наибольшего и наименьшего значений функции на границе области D сводится к отысканию наибольшего и наименьшего значений (абсолютного экстремума) функции одной переменной, так как уравнение границы области D - φ(x,y)=0 связывает переменные x и y между собой. Значит, если разрешить уравнение φ(x,y)=0 относительно одной из переменных или параметрические уравнения границы области D и подставить их в уравнение z=f(x,y), то придем к задаче нахождения наибольшего и наименьшего значений функции одной переменной. Если уравнение φ(x,y)=0 невозможно разрешить относительно одной из переменных или невозможно найти параметрическое задание границы, то задача сводится к отысканию условного экстремума.

13. Задача об объеме цилиндрического тела.

Р ассмотрим в плоскости Оху замкнутую область D, ограниченную линией L, являющейся замкнутой непрерывной кривой. z = l(P) = f(x,y), P= (x,y)  D – произвольные ф-ции определенные и ограниченные на D. Диаметром области D наз. наибольшее расстояние между граничными точками. Область D разбивается на n частых областей D1…Dn конечным числом произв. кривых. Если S – площадь D, то Si – площадь каждой частной области. Наибольший из диаметров областей обозн . В каждой частной области Di возьмем произв. точку Pi (i , Di)  Di, наз. промежуточной. Если диаметр разбиения D   0 , то число n областей Di  . Вычислим зн-ие ф-ции в промежуточных точках и составим сумму:I = f(i, Di)Si (1), наз. интегральной суммой ф-ции. Ф-ция f(x,y) наз. интегрируемой в области D если существует конечный предел интегральной суммы.

Двойным интегралом ф-ии f(x,y) по области D наз. предел интегральной суммы при   0. Обозн:

или

Рассмотрим тело V, которое сверху ограничено поверхностью с образующими, параллельными оси z, снизу – плоской фигурой P на плоскости xy. Требуется найти объём V тела. Разложим область P сетью кривых на части 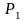, , …, и рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями эти частичные области и в совокупности составляют данное тело. Для подсчета объема отдельных столбиков возьмём произвольно в каждой фигуре по точке: . Если приближенно принять каждый столбик за настоящий цилиндр с высотой, равной аппликате , то объём отдельного столбика оказывается приближенно равным , где означает площадь фигуры. В таком случае приближенное выражение объёма всего тела будет: . Для повышения точности этого равенства будем уменьшать размеры площадок , увеличивая их число. В пределе, при стремлении к нулю наибольшего из диаметров всех областей , это равенство делается точным, так что Предел этого вида и есть двойной интеграл от функции 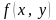по области P. .