1.Определение функции. Способы задания, область определения, геометрическая интерпретация, линии уровня.

Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).

Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.

Геом.интерпр-я :

Каждой точке М₀(х₀; у₀) области D в системе координат Oxyz соответствует точка M(x₀;y₀;z₀), где z₀ = ƒ(х₀;у₀) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=ƒ(x;у).

Способы задания:

1)табличный(для функции двух переменных – в виде таблицы с двумя входами)

2)аналитический(может быть явным: z = x²+y² и неявным: x²+y² +z²-16=0

3)графический (Пусть задана функция f(x,y). Графиком называется множество точек в пространстве , где -абсцисса, - ордината, а - аппликата, т.е. графиком является поверхность.)

Линии уровня: Вид поверхности можно определить с помощью линий уровня, т.е. линий, соответствующих постоянному значению одной из переменных.

2.Предел функции нескольких переменных, понятие повторного предела.z=z(x,y)z=f(x,y) (1)z= (x,y)

Опр1: Ф-я (1) имеет пределом число а при стремлении (x,y) ->(x₀,y₀), если для

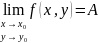(2)Опр2: М(x,y) M₀(x₀,y₀), тогда опр1:Число А нзв пределом ф-и f(M) при , если для

(3) – расстояние (4)Замечание: Указанное опр предела показывает, что f(M) A независимо от того, как M Аналогично обр. можно дать опр. Предела, когда точка , либо Опр3: Число А нзв пределом ф-и f(x,y) при , т.е. Если для 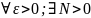, , (5)Данное опр. Предела позволяют как и в случ. ф-и с одной переменной, позволяют сформулировать все теоремы(Алгебра пределов)

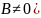( ;Для ф-й двух и большего числа перем. есть понятие повторного предела, (это был двукратный предел).

Понятие повторного предела, когда имеем ряд послед. Пред. Переходов в раздельности в том, или ином порядке.z=f(x,y)найти предел Теорема1(Только формулировка): Если 1) существует конечный (или бесконечный двойной придел) 2) Для сущ. Конечный простой предел x, , то сущ и повторный предел

3. Непрерывность функции нескольких переменных. Разрывы функции нескольких переменных. Свойства непрерывных функций.

Опр.1: Функция z=f(x,y) называется непрерывной в точке M₀, если имеет место след. равенство: (1) В противном случае M₀ – разрыв. При этом M(x,y)→M₀ произвольным образом, оставаясь в области D (области определения функции).Опр.2: Функция z=f(x,y) непрерывна в т. M₀, если для любого ε>0 сущ. такое δ>0, что лишь только |x-x₀|<δ, |y-y₀|<δ, то |f(x,y)-f(x₀,y₀)|<ε. (2)Опр.3: z=f(x,y) непрерывна в M₀, при M(x,y)→M₀(x₀,y₀), если для любого ε>0, сущ. r>0, лишь только ρ(M,M₀)<r, то |f(M)-f(M₀)|<ε. (3)Если в нек. т.M₀ не выполняется (1), то M₀-точка разрыва z=f(x,y). Условие (1) может не выполняться:z=f(x,y) определена во всех точках окрестности некоторой т.M₀, за исключением самой M₀.z=f(x,y) определена во всех точках окрестности точки M₀, но не существует предела.z=f(x,y) определена во всех точках окрестности M₀, существует предел, но не равен значению функции в этой точке.Свойство1: Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения M и наименьшего значения m.Свойство2: Если ф-ция f(x,y,…) непрерывна в замкнутой ограниченной области D и если M, m – наибольшее и наименьшее значения ф-ции в области, то для любого числа μ (m<μ<M), найдется M₀(x₀,y_0,…), что f(x₀,y₀,…)=μ. Следствие: Если ф-ция f(x,y,…) непрерывна в замкнутой ограниченной области и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых ф-ция f(x,y,…) обращается в нуль.Точки разрыва: 1) изолированные; 2) линии разрыва; 3) поверхности разрыва и т.д. Можно показать, что «+, -, ∙, ∕» являются непрерывными функциями.

П-р: следовательно функция разрывная.