Пример доказательства правильности программы методом индуктивных утверждений

Пусть имеется следующая программа поиска максимального значения среди элементов х_i,j.

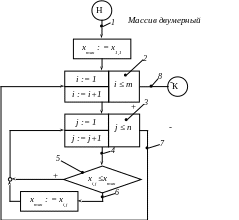
1-8 – это точки, в которых предположительно имеют место следующие утверждения:

• А₁ : х – массив чисел, состоящий из m строк и n столбцов,

(исходная предпосылка);

• А₂ : 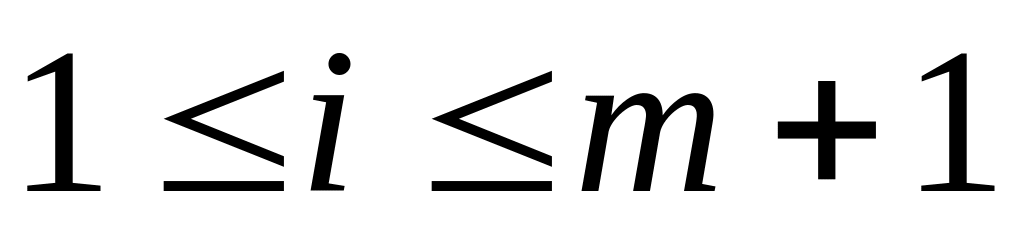, кроме того

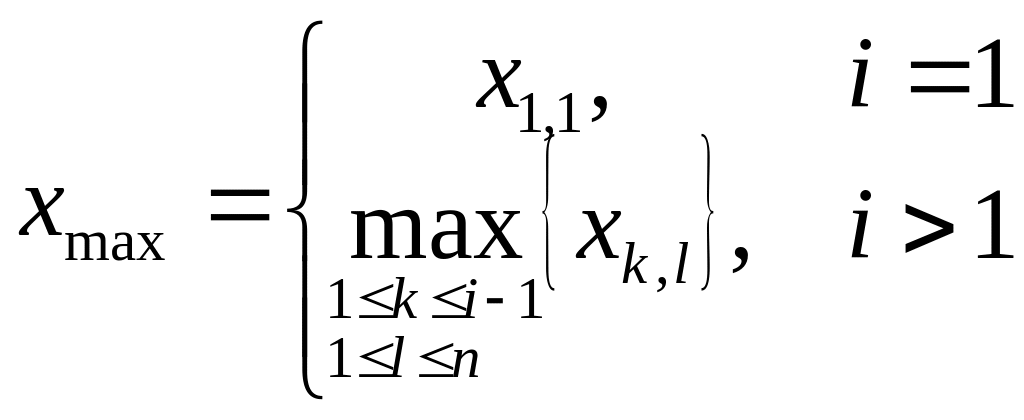
• А₃: 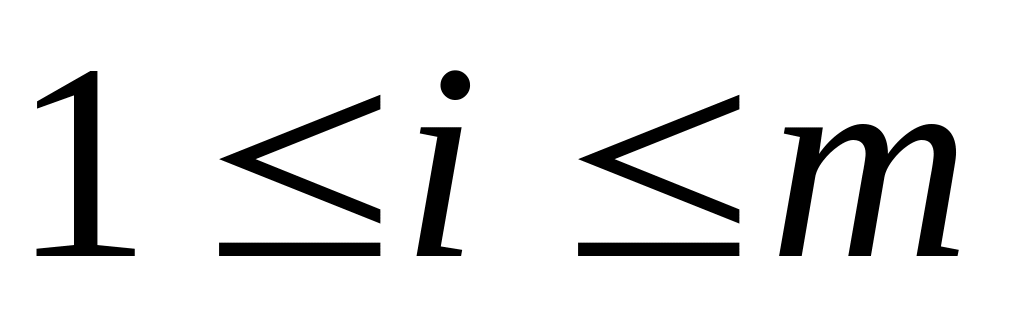, , 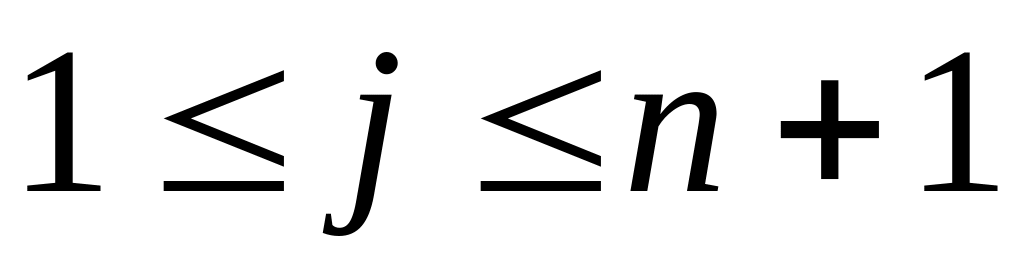при этом .

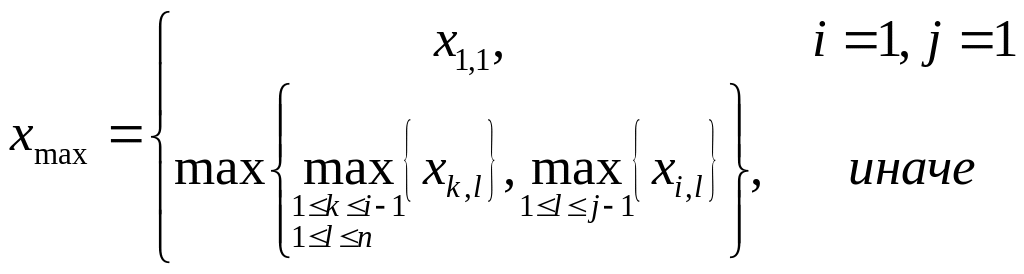• А₈ : .

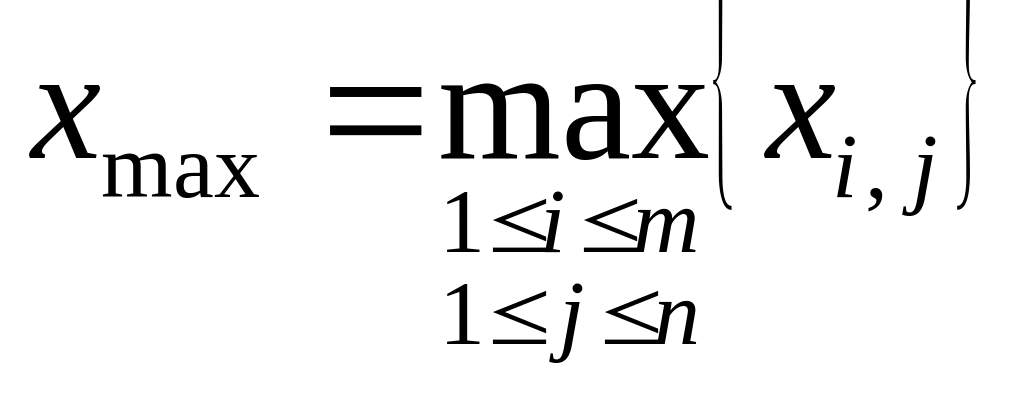Доказательство.

1. Путь 1→2: 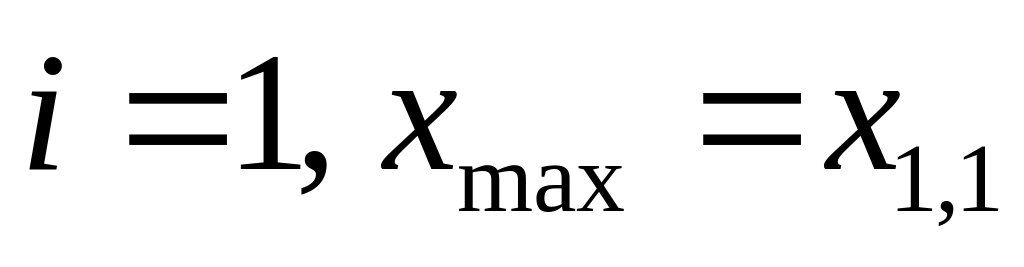, и т.к. из 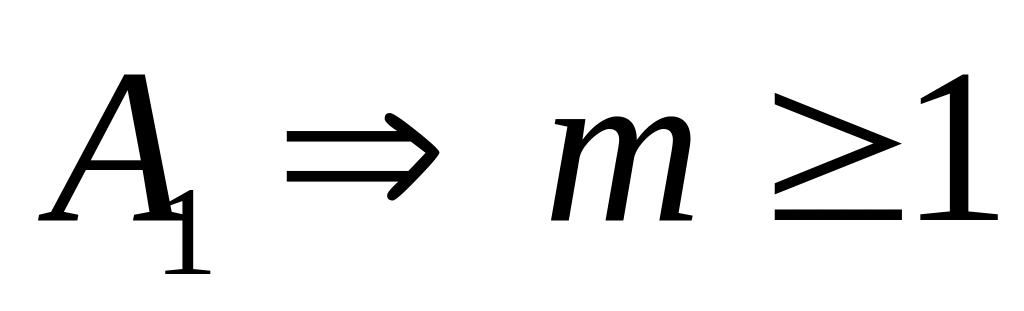, то 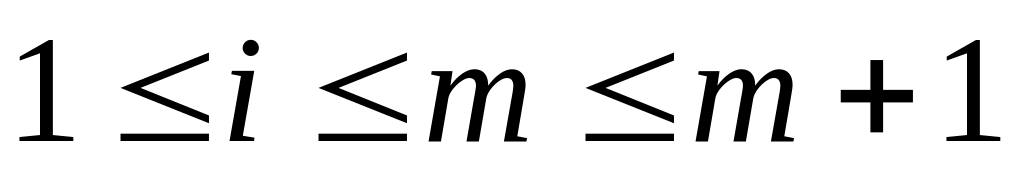, т.е. утверждение А₂ справедливо.

2. Путь 2→3: Дано утверждение А₂. Требуется доказать А₃. При первом вхождении в точку 3 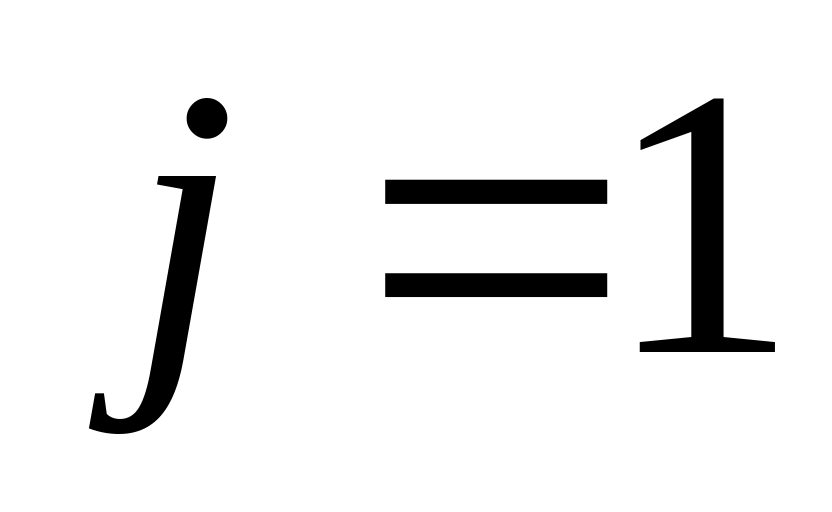,следовательно, 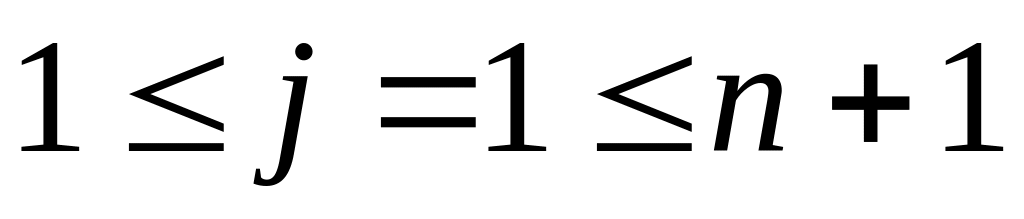, т.к. 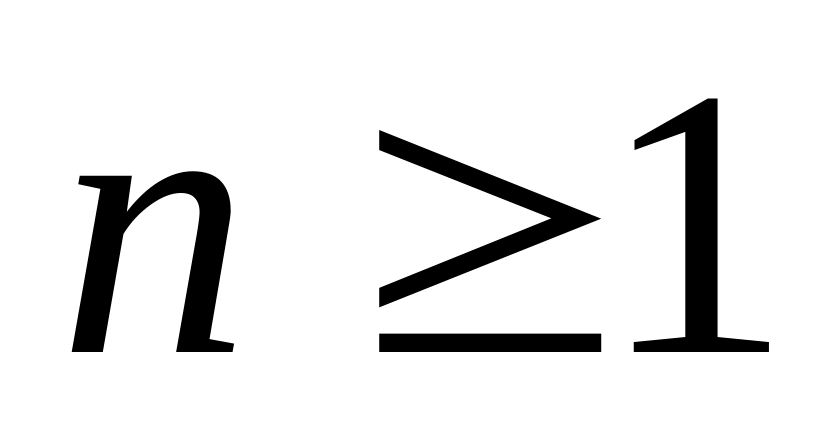. Из утверждения А₂, т.к. i не менялось, имеем , но в силу ограничения цикла в точке 2 в точке 3 получаем . Если 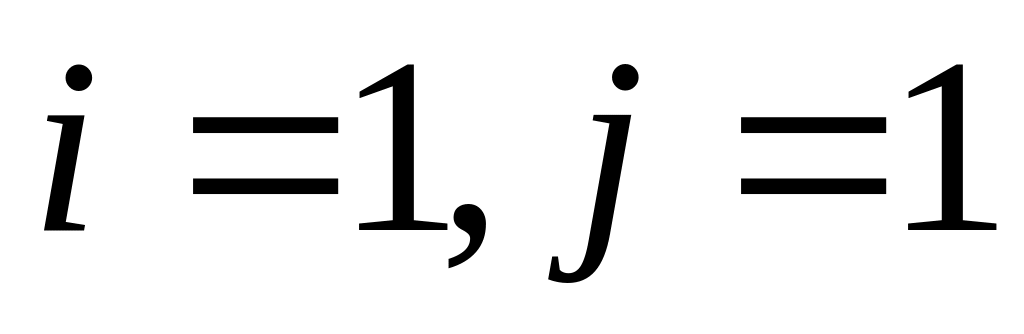, то из утверждения А₂ следует 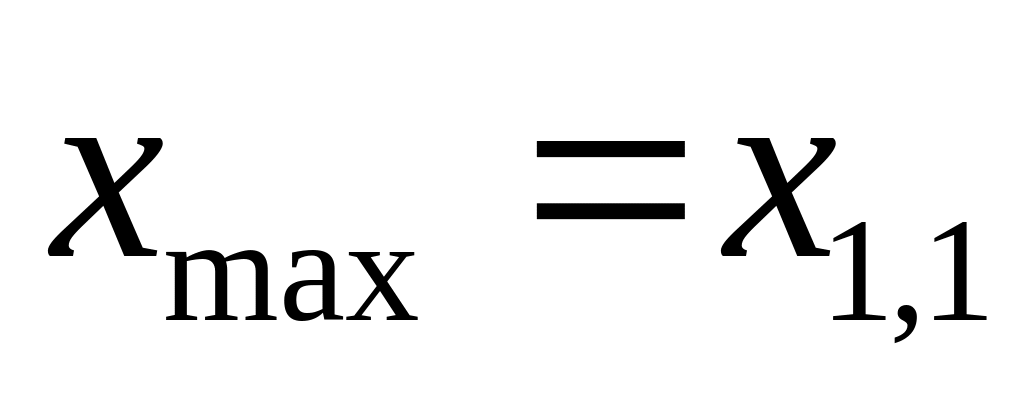, иначе, когда 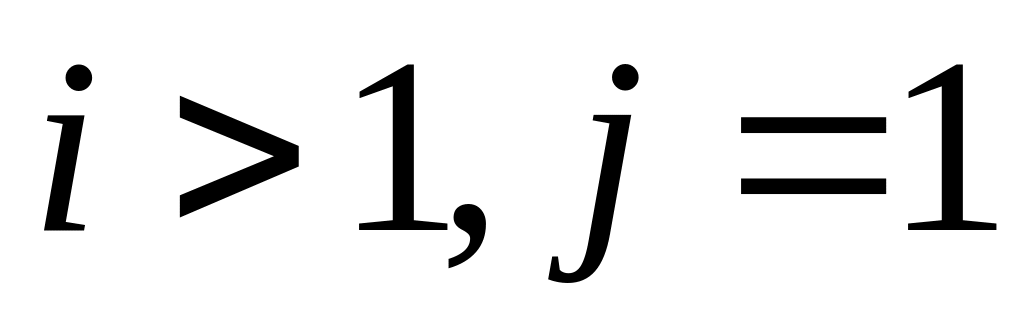, из утверждения А₂ получаем, что 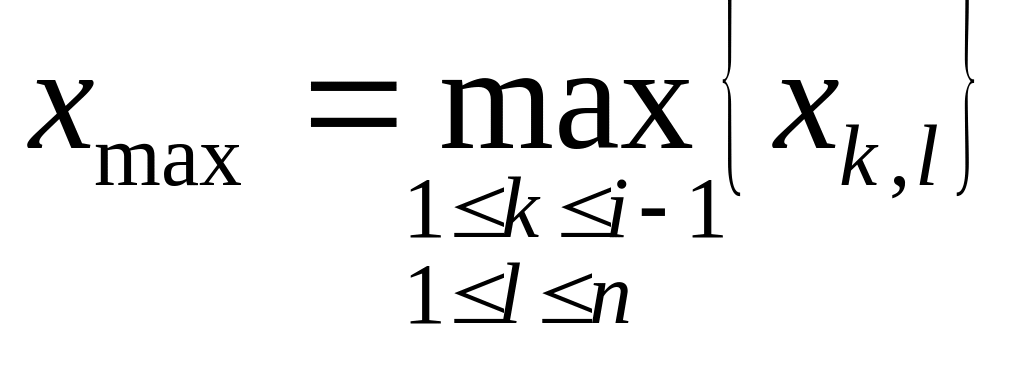. Более того, можно утверждать, что 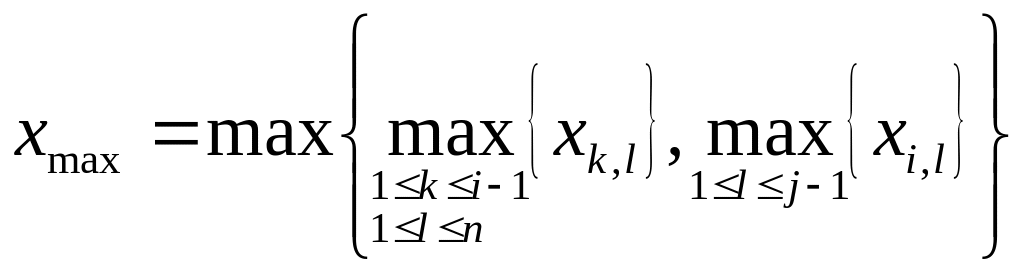, т.к. 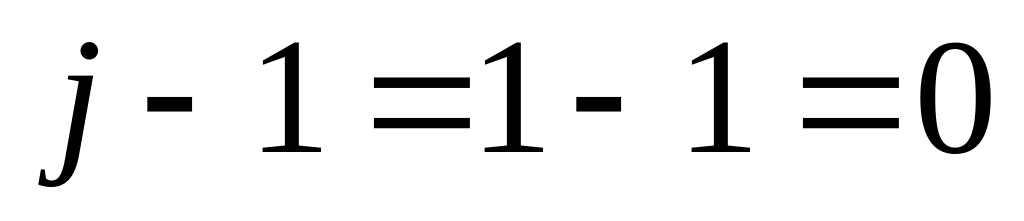. Таким образом, видно, что при переходе из точки 2 в точку 3 утверждение А₃ оказывается справедливым.

3. Путь 3→4→5→3. Пусть справедливо утверждение А₃. Покажем, что оно остается справедливым при переходе по данному пути. Пусть в точке 3 в какой-то момент времени 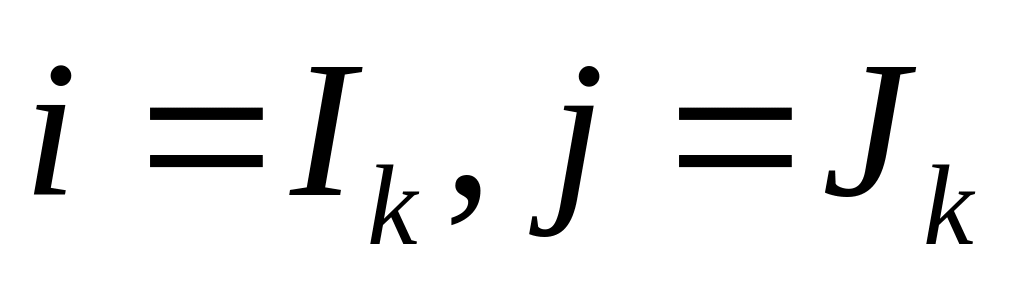, для которых выполняются неравенства: 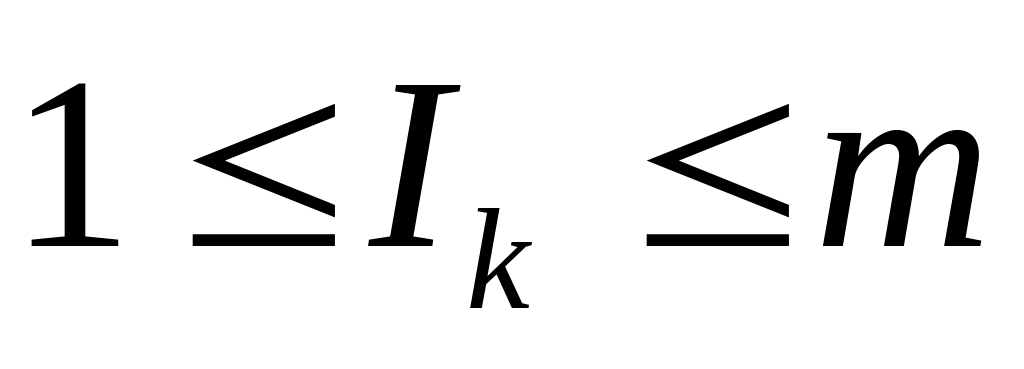, 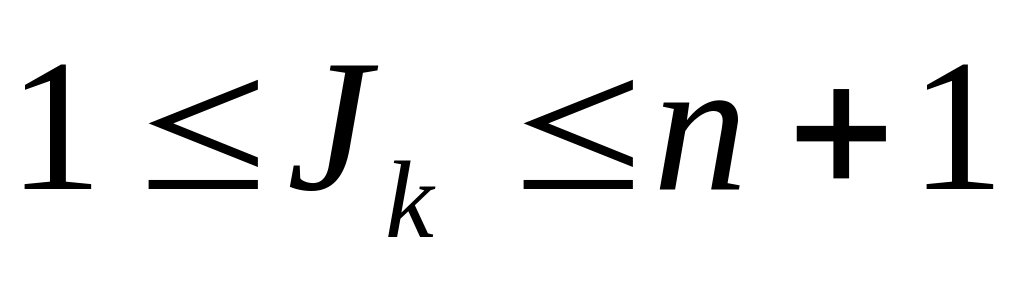. Тогда при переходе по пути 3→4→5→3 получаем 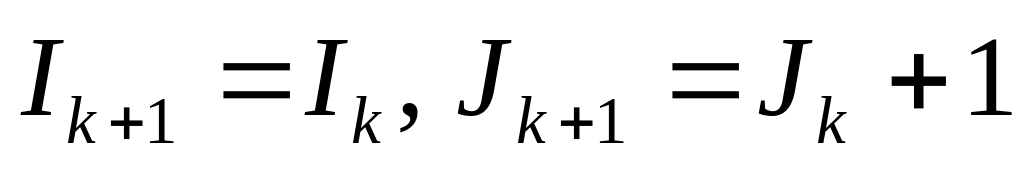, где 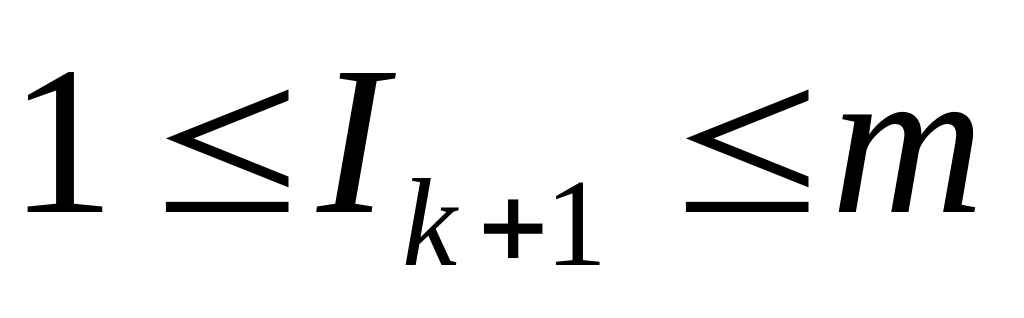. Так как мы двигались по указанному выше пути, то проверка 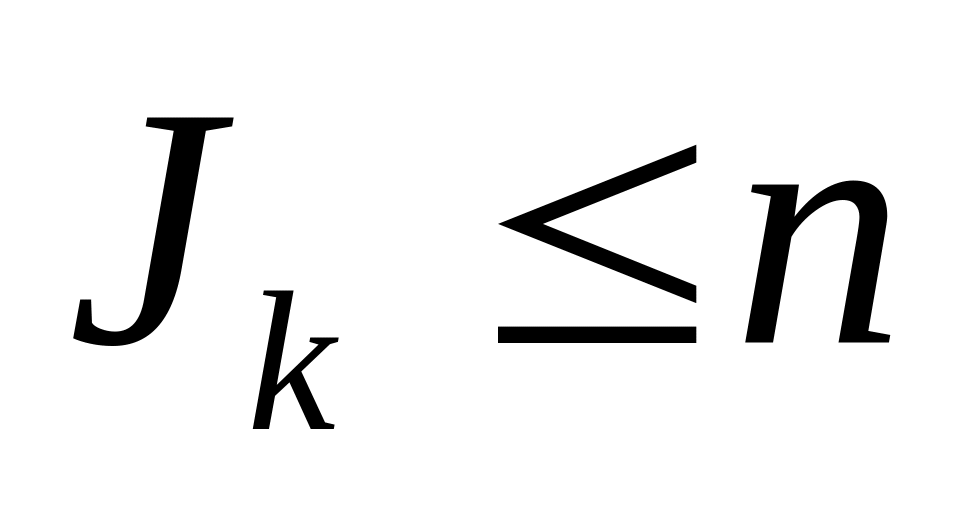в цикле была истинной, следовательно, 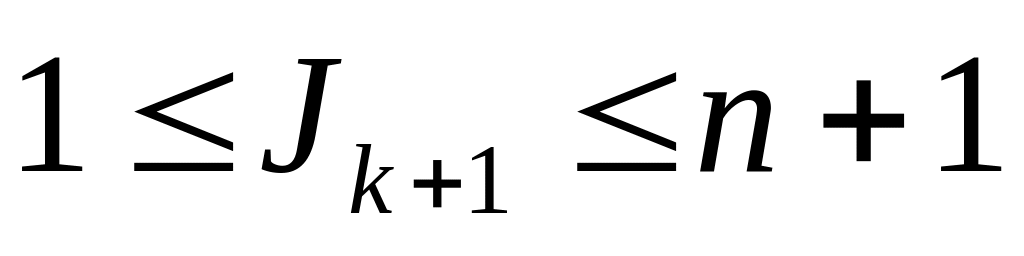. Значение 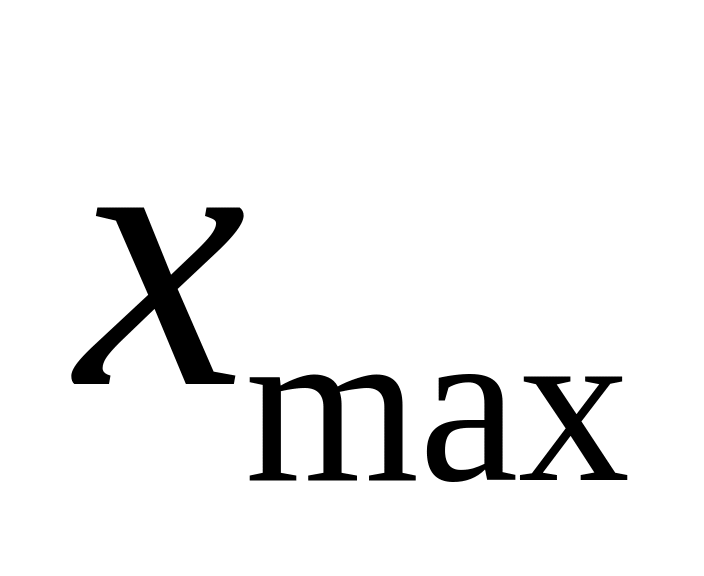не менялось, кроме того, мы приходим в точку 3 с условием 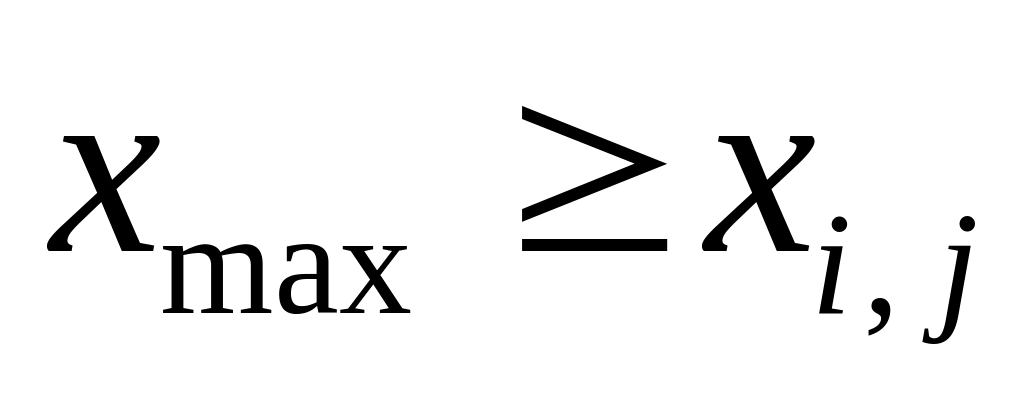, следовательно, остается максимальным и для нового значения j, т.е. утверждение А₃ остается справедливым.

4. Путь 3→4→6→3. Доказательство аналогично пункту 3 за исключением того, что здесь нашлось 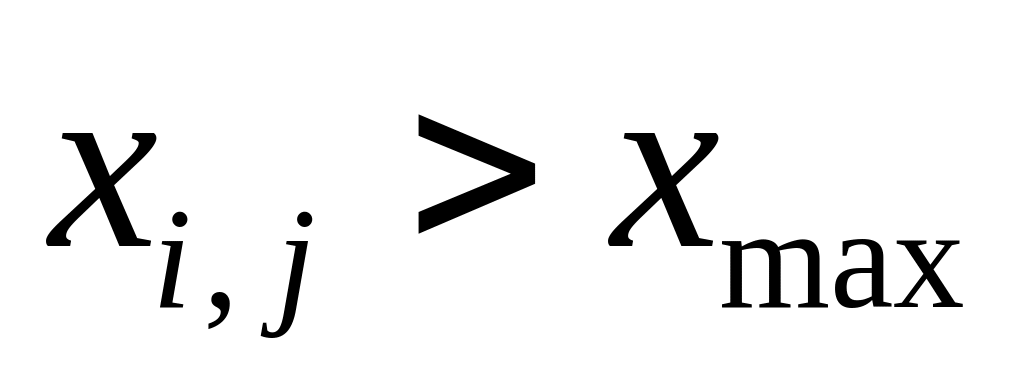, и переменной присвоено это значение. Таким образом, утверждение А₃ остается также справедливым.

5. Путь 3→7→2. Пусть справедливо утверждение А₃. Покажем, что при прохождении пути 3→7→2 будет справедливо утверждение А₂. Из точки 3 в точку 2 мы попадаем, когда ложна проверка , но из А₃ известно, что . Отсюда следует, что 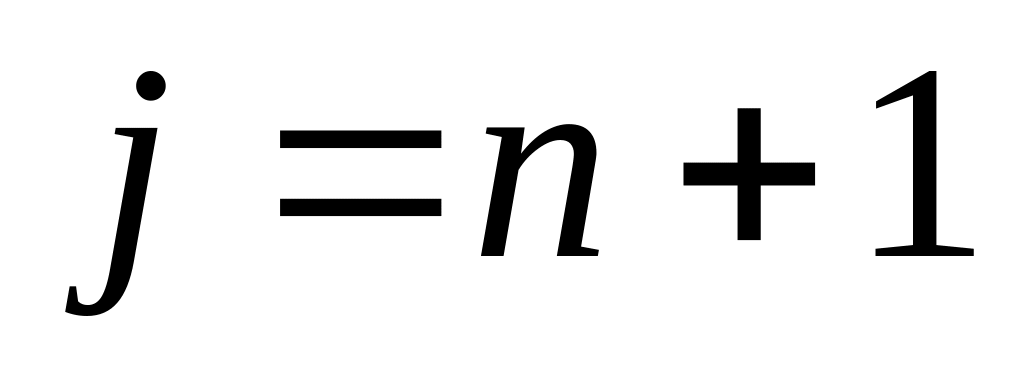или 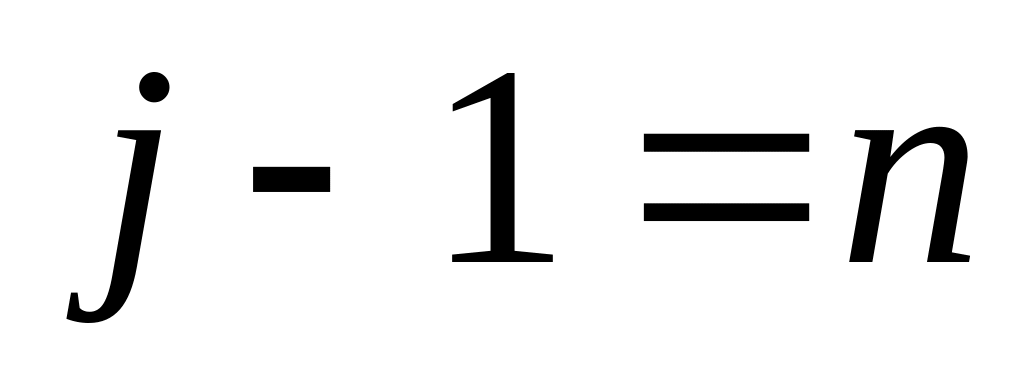. Тогда утверждение A₃ относительно перепишется в виде 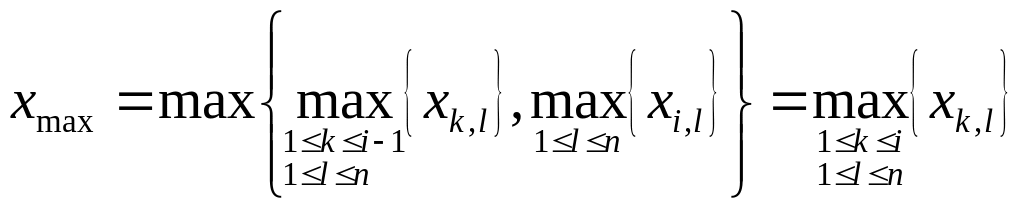. Но при прохождении пути 3→7→2 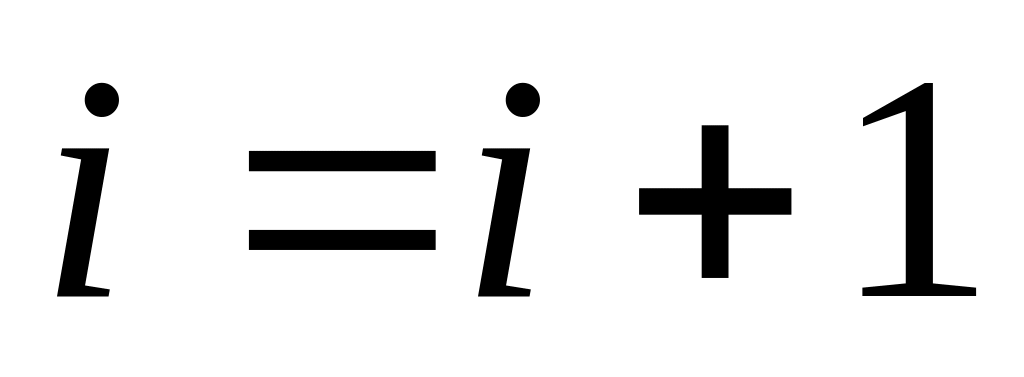, поэтому , . Утверждение А₂ справедливо.

6. Путь 2→8. Так как мы вышли из точки 2 в точку 8 проверка неравенства 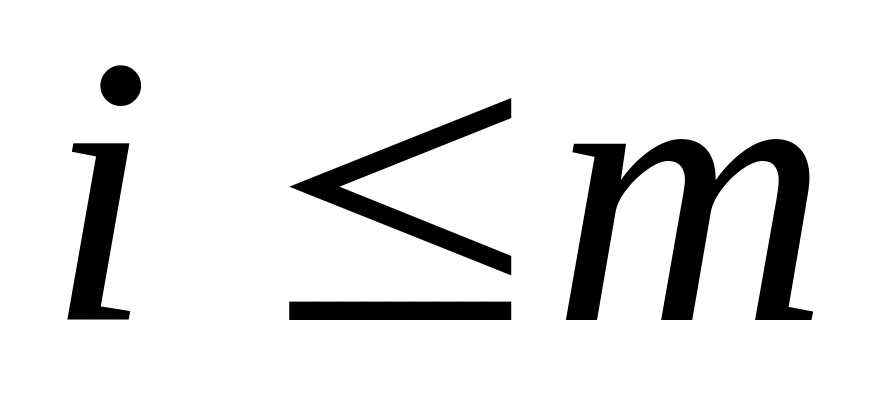оказалась ложной, следовательно, 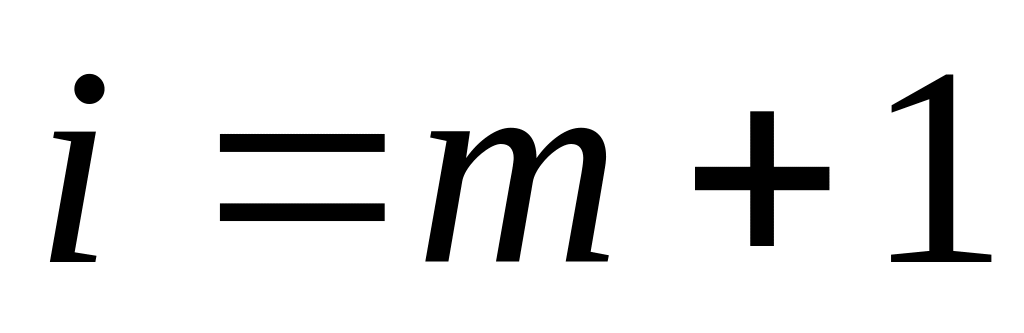и утверждение A₂ , что , преобразуется в утверждение A₈ о частичной правильности программы: .

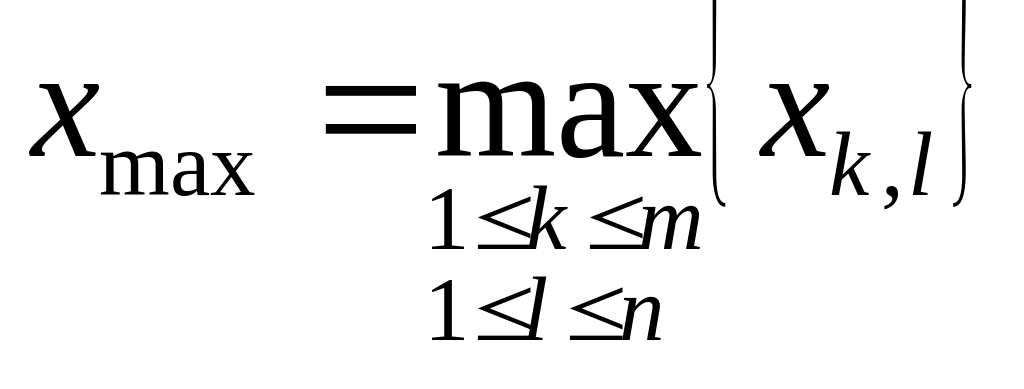Тема 6.Рекурсивные программы. Методы доказательства их правильности

6.1.Понятие рекурсивных программ. Способы их описания Язык описания рекурсивных программ

Введем упрощенный язык программирования для иллюстрации работы рекурсивных программ. Программа на этом языке состоит из определения функции следующего вида:

F (x₁, x₂, … x_n) = if <условие1> then <выражение1>

else if <условие2> then <выражение2>

. . . .

if <условиеN> then <выражениеN>

else <выражение N+1>

В данном выражении последовательно проверяются условия. Если i-ое условие выдает истину, то функция F выдает значение выражения i. Если ни одно из условий не выдает истину, то функция выдает значение выражения N+1. Рекурсия вводится в этот язык следующим образом: функция F может входить как часть в любом из выражений или условий в программе. Такое появление F называется рекурсивным обращением к этой функции. Дополнительно для каждой такой рекурсивной программы необходимо указать область определения, т.е. указать для каких аргументов х₁,…х_n применима программа.