Тема 5.Методы Доказательства правильности программ

5.1.Математический аппарат доказательства Принцип простой индукции

Пусть – некоторое высказывание о целом числе . Требуется доказать, что справедливо для всех .

Согласно простой математической индукции для этого необходимо:

1. доказать, что справедливо высказывание .

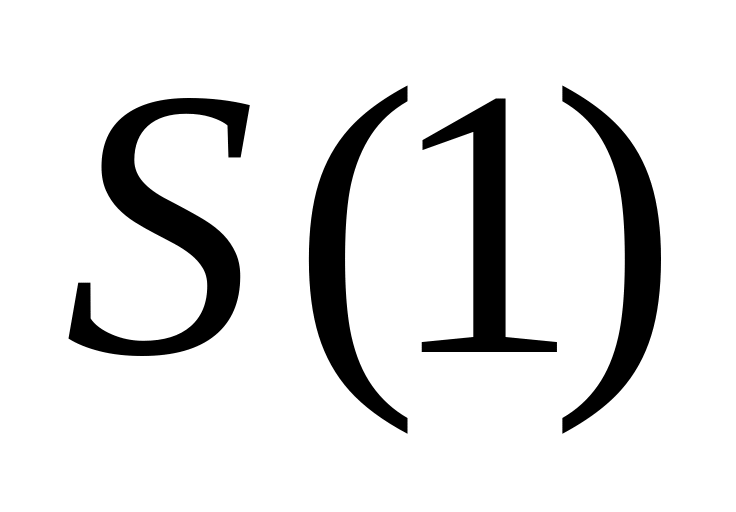2. Доказать, что если для 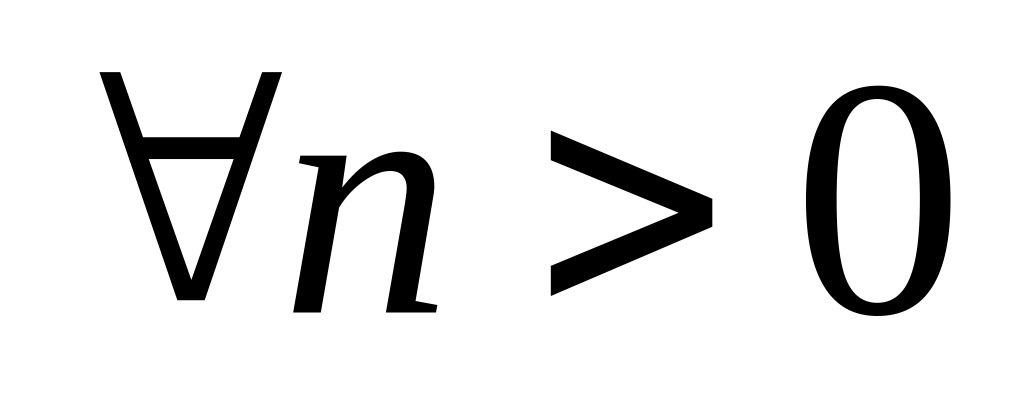справедливо высказывание , то справедливо и высказывание .

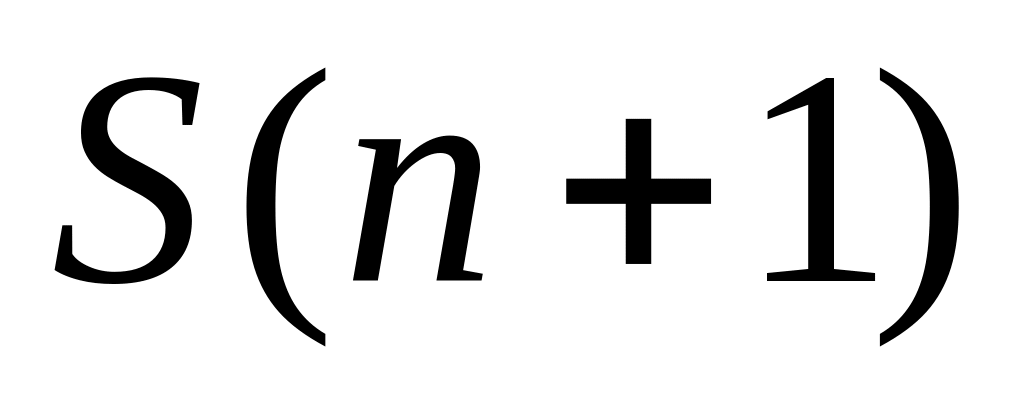Рассмотрим пример использования простой индукции. Необходимо доказать, что для сумма первых положительных целых чисел равна

1. Используя простую индукцию, необходимо доказать, что . Это высказывание справедливо.

2. Предположим, что справедливо высказывание

Покажем, что справедлива формула и для .

Принцип модифицированной простой индукции

Этот принцип применяют, когда необходимо доказать, что утверждение справедливо . В этом случае, чтобы доказать справедливость утверждения необходимо:

1. доказать, что справедливо утверждение ;

2. доказать, что если справедливо , то справедливо и утверждение .

В частном случае при получаем принцип простой индукции.

Иногда необходимо доказать справедливость утверждения . В этом случае можно воспользоваться одним из двух вариантов индукции.

1. Простая восходящая индукция.

Здесь необходимо:

1. доказать, что справедливо утверждение ;

2. доказать, что если справедливо 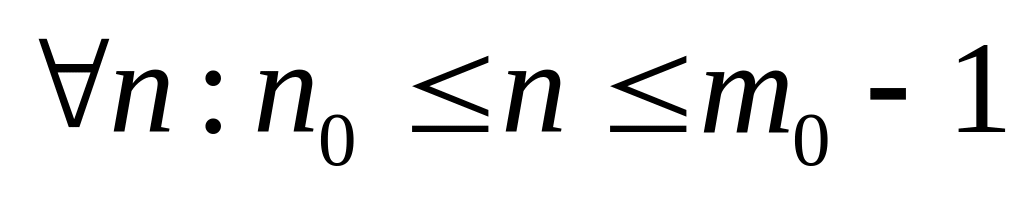, то справедливо и утверждение .

1. Простая нисходящая индукция.

Здесь необходимо:

1. доказать, что справедливо утверждение ;

2. доказать, что если справедливо S(n) 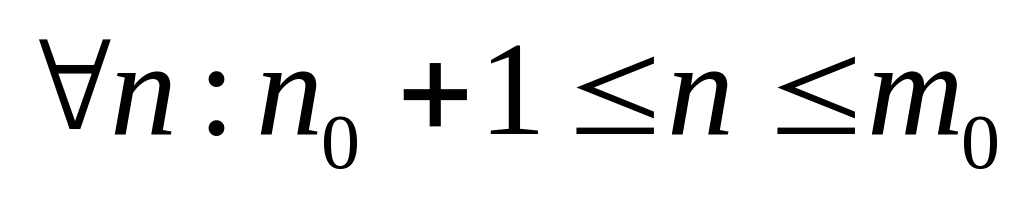, то справедливо и утверждение .

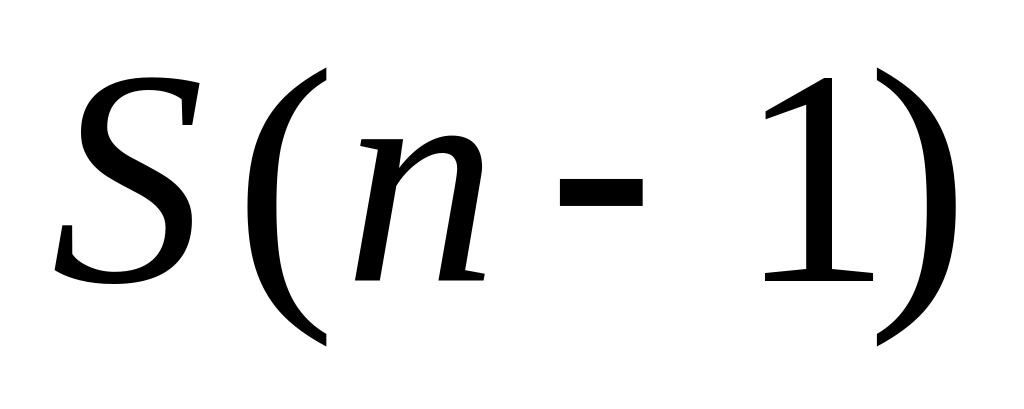Принцип обобщенной индукции

Пусть – некоторое упорядоченное множество, в котором задана операция отношения . Пусть также - минимальный элемент множества. Тогда для доказательства справедливости высказывания необходимо:

1. доказать, что справедливо ;

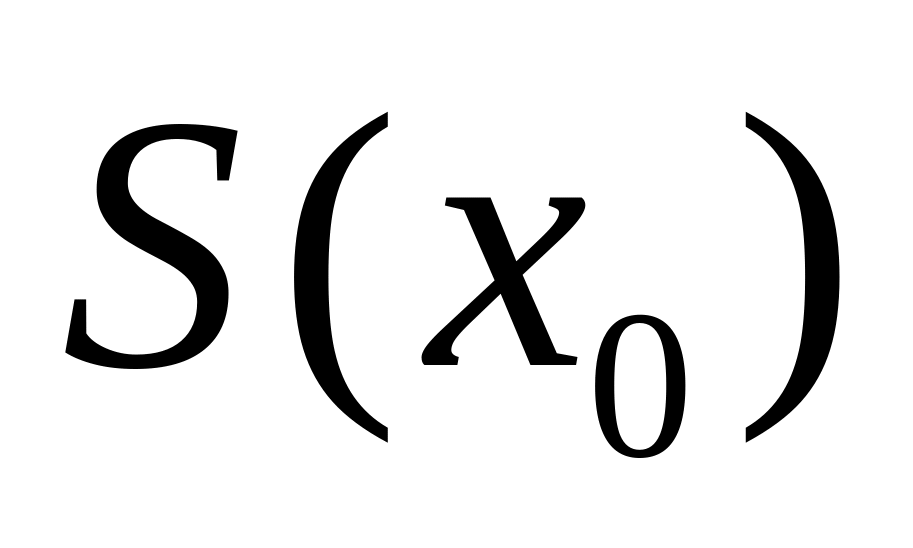2. доказать, что если справедливо , , 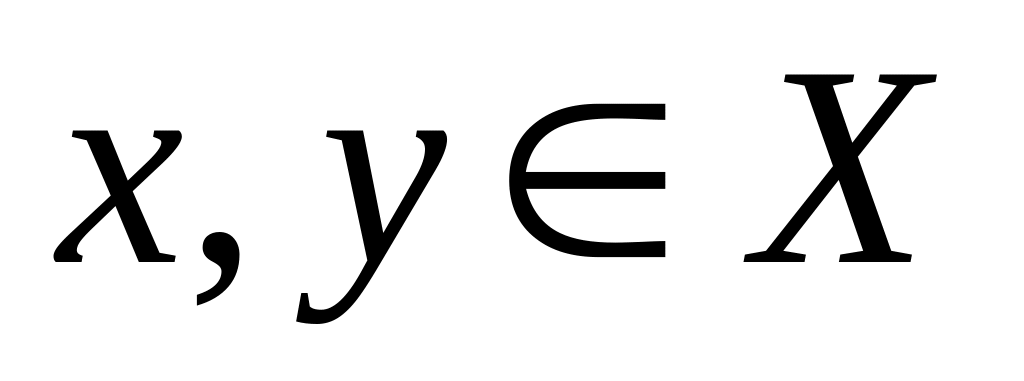то имеет место и .

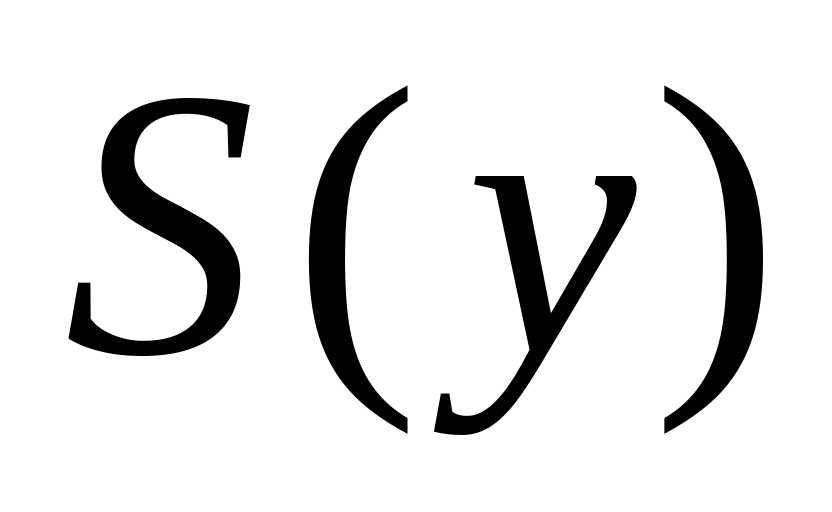5.2.Методы доказательства правильности программ Метод индуктивных утверждений

Определение 1. Пусть А – некоторое утверждение, описывающее предполагаемые свойства данных в программе. С – утверждение, описывающее то, что мы по предположению должны получить в результате процесса выполнения программы, т.е. утверждение о правильности. Будем говорить, что программа частично правильна по отношению к А и С, если при каждом выполнении этой программы с данными, удовлетворяющими А, будет справедливо С при условии, что программа закончит свою работу, т.е. если выполнять программу с данными, удовлетворяющими утверждению А, то либо она не заканчивается, либо заканчивается, и будет справедливо С.

Определение 2. Будем называть программу полностью правильной по отношению к А и С, если она частично правильна и заканчивается при всех данных, удовлетворяющих А.

Для доказательства частичной правильности программы поступают следующим образом:

1. утверждение А связывают с началом программы, а утверждение С – с конечной точкой программы;

2. выявляют некоторые закономерности, относящиеся к значениям переменных, и связывают соответствующие утверждения с другими точками программы;

3. для каждого пути, ведущего из точки i, связанной с утверждением А_i, в точку j, связанную с утверждением А_j, доказывают, что если попасть в точку i и при этом будет справедливо утверждение А_i, а затем пройти в точку j, то будет справедливо утверждение А_j. Для циклов точки i и j могут быть одной и той же точкой.

Если справедливо А₁, то при прохождении по пути 1→2 будет справедливо А₂ и т.д.

Чтобы убедиться, что таким образом действительно доказывается частичная правильность, докажем теорему.

Теорема. Если можно выполнить все действия, описанные в методе индуктивных утверждений для некоторых программ, то эта программа частично правильна относительно А и С.

Доказательство будем проводить с помощью индукции по n - числу точек программы, через которые мы уже прошли.

1. Предположим, что в процессе выполнения программы мы попали в первую из точек n=1. Нужно показать, что связанные с этой точкой утверждения справедливы. Но первая точка – это начальная точка программы, и с ней связано исходное допущение А о начальных данных. Это допущение предполагается справедливым, т.е. для n=1 утверждение справедливо.

2. Предположим, что мы прошли n точек и попали в некоторую точку i_n, с которой связано утверждение . Предположим, что утверждение справедливо (гипотеза индукции). Нужно доказать, что если выполнение программы продолжается, и мы из точки i_n попали в точку i_n+1, то при ее достижении будет справедливо утверждение . Справедливость этого факта для каждого пути, связывающего точки i_n и i_n+1, мы доказали в методе индуктивных утверждений (пункт 2). Таким образом, если программа написана по правилам структурного программирования и является простой, то для каждой точки i будет справедливо утверждение А_i, так как существует путь через каждый узел от начала к концу программы. Тогда, если будет достигнута конечная точка программы, то будет справедливо и утверждение С.