4.2.Теорема о структурировании

Теорема. Любая простая программа функционально эквивалентна программе, составленной из элементов базисного множества: последовательность, if then else, whilе do с использованием функций и предикатов исходной программы, а также присваиваний и тестов над дополнительным счетчиком.

Доказательство (конструктивное). Рассмотрим произвольную простую программу с произвольным числом функциональных предикатных узлов, пронумерованных от 1 до n. Номер 1 соответствует входной линии программы. Выходной линии программы присвоим номер 0. Дадим выходным линиям каждого функционального и предикатного узла номер следующего функционального или предикатного узла. Если выходная линия соответствует выходной линии программы, то ей присвоим номер 0.

Д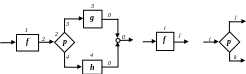 алее для каждого функционального узла h, имеющего номер i и выходную линию j, составим в соответствие новую элементарную программу (последовательность) g_i с номером входной линии i.

З десь в новом функциональном узле производится присваивание номера выходной линии переменной L, называемой программным счетчиком. Далее для каждого предикатного узла с номером i и выходными линиями j и k поставим в соответствие элементарную программу g_i вида:

Т еперь построим программу типа «whilе do» следующего вида:

Т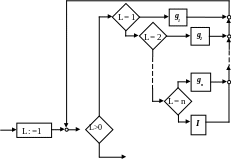 аким образом, какой бы ни была исходная простая программа, мы можем получить функционально эквивалентную ей структурированную программу. Такая программа называется помеченной структурированной программой.

П ример. Пусть требуется построить помеченную структурированную программу для следующей программы.

Элементарные программы g_i для нее будут иметь вид:

П одставив g₁ – g₄ в схему, сконструированную в доказательстве теоремы, получим блок-схему структурированной программы.

4.3.Рекурсивные структурированные программы

Предыдущие способы получения структурированных программ могут быть недостаточно понятными и эффективными. Для их усовершенствования вводится другой способ, исключающий излишние установки и проверки счетчика L. Идея заключается в том, чтобы для каждого j>0 заменить все присваивания вида L:= j соответствующей программой g_j.

Поскольку значение j тем самым никогда не будет присвоено счетчику L, проверка L=j может быть вынесена за пределы последовательности структур if then else. Допустим, имелась последовательность программ g₁; g₂;… g_n. Один шаг, описанной выше замены, приводит к новой последовательности программ . Здесь при необходимости могут быть перенумерованы. Единственным препятствием продолжению этого процесса может быть рекурсивное обращение, когда некоторые будут содержать присваивание L=i.

Таким образом, процесс замещения можно продолжать до тех пор, пока:

1) все присваивания счетчику L, кроме L:=0, не будут замещены;

2) каждая оставшаяся программа будет содержать лишь присваивания L= i.

Если программа ациклическая, то на каждом пути появится присваивание L:=0. Следовательно, в этом случае счетчик L и цикл whilе L>0 do могут быть исключены.

Рассмотрим в качестве примера следующую структурированную программу с программным счетчиком:

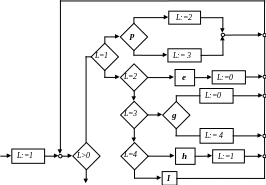
На первом шаге присваивание L:=4 заменим программой, стоящей на пути L:=4 (последовательность h, L:=1). Поскольку после этого присваивание L:=4 нигде не будет встречаться, проверку L=4 можно будет исключить. В результате получим следующую программу:

Д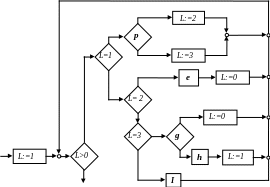 алее производим замену узла L:=2 на последовательность е, L:=0, а узел L:=3 заменяем на программу, стоящую на пути L=3. В результате будем иметь:

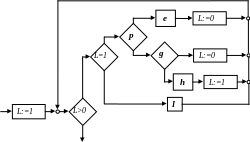
Здесь можно заметить, что присваивание L:=1 и проверку L=1 можно также исключить, так как L становится равным 1 только на выходе из цикла. Поэтому программа будет выглядеть следующим образом: