4.5. Кинематическое исследование траекторий самонаведения с использованием метода погони

Для выяснения основных свойств кривых погони предполагается, что летательный аппарат и цель движутся в одной плоскости, причем траектория цели является прямолинейной. Кинематические уравнения движения при этом имеют вид [9]

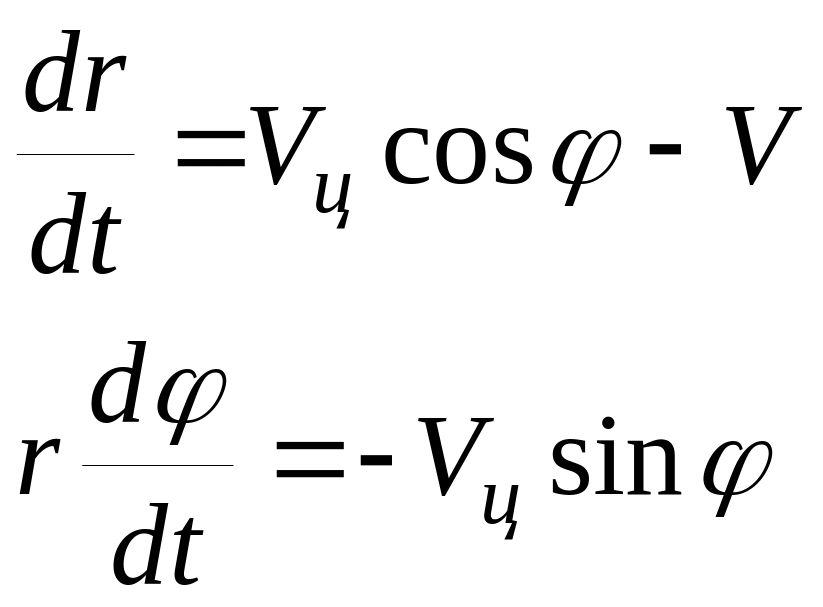
где r-радиус вектор между ЛА и целью; Vц-скорость цели; V-скорость ЛА; -угол, между линией визирования ЛА и земной осью.

Требуется исследовать кинематические системы для следующего диапазона начальных условий

r=2-15км; Vц=250-600м/с; Vо=250-600м/с, скорость V увеличивается до 500-1400м/с, _о=0-180^о.

Программа должна обеспечивать визуализацию задания условий движения цели и самого наведения, в том числе построение графиков r(t), (t), r()

4.6. Нахождение переходной (фундаментальной) матрицы для системы линейных уравнений

Рассматривается однородное дифференциальное уравнение для линейной системы

,

где А-матрица размерности nxn, x – вектор состояния размерности nx1.

Решение представленного уравнения может быть записано в виде

где Ф называется переходной (фундаментальной) матрицей исходной системы. Фундаментальная матрица является решением дифференциального уравнения

В случае, если коэффициенты матрицы А постоянны, то фундаментальная матрица может быть определена по формуле

Требуется создать программный модуль расчета переходной матрицы указанными выше методами и, на его основе, решить задачу прогнозирования вектора состояния стационарного ИСЗ на круговой орбите. Уравнения движения стационарного ИСЗ (СИСЗ) рассматриваются в абсолютной геоцентрической инерциальной системе координат и имеют следующий вид:

При решении широкого круга задач навигации, управления и связанных с ними задач анализа точности чрезвычайно удобны уравнения движения ИСЗ, получаемые путем линеаризации нелинейных уравнений. В результате получают систему вида

Для СИСЗ:

=1/86164.03 - угловая скорость вращения Земли.

- радиус круговой орбиты.

Интервал времени – 0.5 и 1 сутки

5. Методика программирования

Библиотека Simulate 1.0 содержит набор модулей, в которых представлены классы Object Pascal, реализующие объектно–ориентированное представление сложных динамических систем и их элементов. Методические указания по применению этой библиотеки для решения задач интегрирования дифференциальных уравнений приведены в пособии [1]. Чтобы сделать модули библиотеки доступными проекту необходимо:

1. Создать проект

2. Выбрать в меню Delphi команду Project/Options

3. На закладке Directories/Conditionals в строке Search path ввести Z:\Simulate1\Units

4. Создать новый модуль (New/Unit) и в нем объявить классы, реализующие математическую модель задачи как наследников подходящих классов библиотеки Simulate 1.0. В раздел uses модуля необходимо добавить ссылки на следующие модули

uCommon – общематематические процедуры и функции

uCustom – базовые классы математических моделей

uVector – векторы и матрицы.

5. Создать форму главного окна (и другие, если это необходимо), в которых реализовать отклики на действия (команды меню, кнопки и т.п.).

Рассмотрим методику составления программы на следующем примере.

Космический аппарат (КА) совершает некомпланарный перелет при непрерывно действующем малом реактивном ускорении. Математическая модель его движения представлена системой дифференциальных уравнений в безразмерных переменных:

(1)

где r –безразмерное расстояние между КА и центром Земли; u, V – безразмерные составляющие орбитальной скорости, направленные по радиусу и нормали к нему в плоскости движения;   долгота восходящего узла;   аргумент перигея;   истинная аномалия. При этом безразмерная скорость связана с радиусом соотношением .

Безразмерные составляющие управляющего ускорения заданы функциями

, , , (2)

где . (3)

Здесь Т – безразмерное время перелета; t  безразмерное текущее время; a  номинальное безразмерное ускорение. Отметим, что безразмерное время перелета можно задать как , где N  число полных оборотов вокруг Земли, совершаемых КА в процессе перелета.

Составляющие ускорения выбраны так, что радиус орбиты будет возрастать, а наклонение – уменьшаться. Пусть начальные условия для всех углов кроме наклонения  нулевые, т.е. u(0)=(0)=(0)=(0)=0, а начальные условия по радиусу и наклонению задаются пользователем.

Необходимо моделировать движение КА на заданном интервале времени и получить зависимости параметров его орбиты по времени.

Структуризация задачи проводится с использованием понятий «главная система» и «подсистема», принятых в [1].

Зависимости ускорения от времени, т.е.  алгоритм управления движением КА, целесообразно выделить в отдельный объект - подсистему. Это даст возможность замены одного алгоритма управления на другой без изменения объекта, реализующего уравнения движения.

В качестве главной системы данного примера выберем дифференциальные уравнения движения (1), а в качестве подсистемы  «блок управления», который описывается уравнениями (2), (3).

Поскольку математическая модель главной системы нашего примера представляет собой систему обыкновенных дифференциальных уравнений, она должна быть наследником класса TDifEquation. Подсистема «блок управления» описывается функциями времени. Поэтому ее можно реализовать наследником TDynamicObject.

Ниже приведен листинг модуля MyModel (см. шаг 4 методики) с классами данного примера. Здесь объявлены два класса:

TController – отвечает за вычисление составляющих управления согласно (2),(3)

TOrbitModel – инкапсулирует уравнения движения (1).

unit MyModel;

interface

uses uCommon,uCustom;

type

TController = class;

TOrbitModel = class(TDifEquation)

private

FControl : TController;

FArgLat : TFloat;

public

constructor Create;

procedure Dynamics; override;

procedure PreCompDynamics; override;

property ArgLat : TFloat read FArgLat;

property Control : TController read FControl;

end;

TController = class(TDynamicObject)

private

FOrbitModel : TOrbitModel;

FAr,Fan,Fat :TFloat;

public

Anom : TFloat;

procedure Dynamics; override;

property Ar : TFloat read FAr;

property An : TFloat read FAn;

property At : TFloat read FAt;

end;

implementation

uses Math; // математический модуль Delphi

constructor TOrbitModel.Create;

begin

inherited Create(7,7);

FControl := TController.Create;

FControl.FOrbitModel:= Self;

AddMember(FControl);

end;

procedure TOrbitModel.Dynamics;

var AnV : TFloat;

begin

AnV := FControl.An/X[3];

DxDt[1] := X[2];

DxDt[2] := Sqr(X[3])/X[1] - 1/Sqr(X[1]) + FControl.Ar;

DxDt[3] := - X[2]*X[3]/X[1] + FControl.Af;

DxDt[4] := AnV * Sin(FArgLat)/Sin(X[5]);

DxDt[5] := AnV * Cos(FArgLat);

DxDt[6] := -AnV*Sin(FArgLat) * CoTan(X[5]);

DxDt[7] := X[3]/X[1];

end;

procedure TOrbitModel.PrecompDynamics;

begin

FArgLat := AngleTo2Pi(X[6]+X[7]);

end;

procedure TController.Dynamics;

var Lambda : TFloat;

begin

Lambda := HalfPi /TermTime * SysTime;

Ar := 0;

Af := Anom * Cos(Lambda);

An:=-Anom*Sin(Lambda)* Sign(Cos(FOrbitModel.ArgLat));

end;

end.

Связь основной модели (т.е. уравнений движения) с блоком управления осуществляется следующим образом. Объект TOrbitModel имеет скрытое поле FControl, доступное через свойство Control в режиме чтения. В свою очередь, объект TController имеет поле FOrbitModel, содержащее ссылку на объект TOrbitModel. При создании объекта TOrbitModel ее конструктор сначала вызывает наследуемый конструктор, который устанавливает размер вектора производных и вектора зависимых переменных равный 7 (по числу дифференциальных уравнений модели движения). Затем создается объект TController и ссылка на него запоминается в поле FControl. После этого полю FOrbModel объекта TController присваивается ссылка на модель, а сам блок управления добавляется в список подсистем модели движения. Таким образом, необходимые связи установлены.

Отметим, что явные ссылки введены в данном примере исключительно ради наглядности. Так, при добавлении любой подсистемы в список, ее владельцем автоматически становится основная модель. Поэтому любая подсистема может получить доступ к системе верхнего уровня по ссылке Owner. С другой стороны, основная модель может «найти» свою подсистему обращением к свойству Member[Index].

Обратимся к уравнениям движения и алгоритму управления. Нетрудно видеть, что правых частях модели движения и в уравнениях блока управления несколько раз встречается сумма (+) – аргумент широты КА. Целесообразно вычислять это значение один раз и сделать доступным не только самой модели, но и блоку управления. Для этого объект TOrbMdel имеет свойство ArgLat доступное любому другому объекту в режиме чтения. Так как аргумент широты должен быть доступен до расчета производных и управляющего воздействия, его значение вычисляет виртуальный метод PreCompDynamics объекта TOrbModel. Отметим, что аргумент широты при интегрировании системы (1) будет непрерывно возрастать от начального значения (в нашем случае  от нуля) до 2N. Метод PreCompDynamics приводит текущее значение аргумента широты к диапазону [0..2] с помощью вспомогательной функции AngleTo2Pi, импортируемой из модуля uCommon. Константы TwoPi=2 и HalfPi=/2 также импортитуются из модуля uCommon.

Вычисление правых частей уравнения движения (1) реализует метод TOrbModel.Dynamics. Здесь каждой зависимой переменной модели т.е. свойству X[index] соответствует производная DxDt[index]. Считается, что индекс зависимой переменной есть порядковый номер уравнения системы (1), начиная с 1.

Объект TController реализует алгоритм управления (2), (3). Его свойства предствляют собой:

Anom  номинальное реактивное ускорение;

Ar  радиальная составляющая ускорения;

At  трансверсальная составляющая ускорения;

An  бинормальная составляющая ускорения.

Алгоритм управления запрограммирован в методе Dynamics класса TController.

Форма главного окна имеет следующий вид.

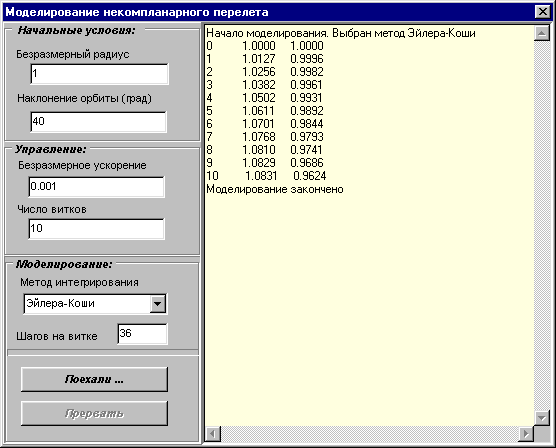
Здесь предусмотрен как ввод начальных условий движения КА, так и выбор метода численного интегрирования.

Листинг модуля главной формы представлен ниже. Обратите внимание на комментарии.

unit Form1;

// Пример программы моделирования некомпланарного перелета КА

// с непрерывной малой тягой

// с Федоров А.В. 1999

interface

uses

Windows,Messages,SysUtils,Classes,Graphics,Controls,Forms,

Dialogs,StdCtrls,ExtCtrls,

uCustom;

type

TForm1 = class(TForm)

Panel1: TPanel;

GroupBox1: TGroupBox;

Label1: TLabel;

Label2: TLabel;

edRadius: TEdit; // Редактор начального радиуса

edInclination: TEdit; //Редактор начального наклонения

GroupBox2: TGroupBox;

Label3: TLabel;

Label4: TLabel;

edAccelerat: TEdit; // Редактор номинального ускорения

edRevol: TEdit; // Редактор числа витков

Panel2: TPanel;

Panel3: TPanel;

Memo1: TMemo;

GroupBox3: TGroupBox;

Label5: TLabel;

edOrbitSteps: TEdit;//Редактор числа шагов на витке

bRun: TButton; //Кнопка «Поехали...»

bCancel: TButton;//Кнопка «Прервать»

Bevel1: TBevel;

cbMethod: TComboBox; // Список методов интегрирования

Label6: TLabel;

//Обработчики событий кнопок и формы

procedure bRunClick(Sender: TObject);

procedure bCancelClick(Sender: TObject);

procedure FormCreate(Sender: TObject);

private

{ Общие поля, доступные форме и симулятору }

FOut : TextFile; // Текстовый файл результатов

FSim : TSimulator; // Симулятор

FOrbSteps : integer; // Число шагов на витке

FCancel : boolean; // Флаг принудительного выхода

FMethodIndex : integer; // Индекс метода интегрирования

public

// Обработчики событий симулятора

procedure OnEnterSim(Sender:TObject);

procedure OnExitSim(Sender:TObject);

procedure OnOutputSim(Sender:TObject);

procedure OnStopSim(Sender:TObject; var Stop:boolean);

end;

var

Form1: TForm1;

implementation

uses uCommon,MyModel;

{$R *.DFM}

procedure TForm1.OnEnterSim(Sender:TObject);

// Обработчик события симулятора OnEnter.

begin

// При входе в симулятор очищаем Memo1

Memo1.Clear;

// выводим строку-заголовок в Мемо1

Memo1.Lines.Add('Начало моделирования. Выбран метод '+

cbMethod.Text);

// Открываем выходной файл, имя которого связано с методом

// интегрирования

case FMethodIndex of

0: AssignFile(FOut,'Euler.dat');

1: AssignFile(FOut,'RK4.dat');

end;

// Очищаем файл результатов и выводим строку-заголовок

Rewrite(FOut);

Writeln(FOut,'N':3,'R':10,'Vr':10,'Vs':10,'Om':10,

'I/Io':10);

// Сброс флага принудительного завершения моделирования

FCancel := false;

end;

procedure TForm1.OnExitSim(Sender:TObject);

// Обработчик события симулятора OnExit

begin

// По окончании моделирования закрываем файл результатов

CloseFile(FOut);

// и выводим строку в Мемо1

Memo1.Lines.Add('Моделирование закончено');

end;

procedure TForm1.OnOutputSim(Sender:TObject);

// Обработчик события OnOutput

var k : integer;

CurRev : integer;

S : string;

RelIncl : TFloat;

begin

// Вывод результатов осуществляется в конце витка

if FSim.Method.CurIter mod FOrbSteps = 0 then

begin

// Вычисляем номер текущего витка

CurRev := Trunc(FSim.Method.CurIter/FOrbSteps);

// Вычисляем отношение текущего наклонения к начальному

RelIncl := FSim.Model.State[5].AsFloat/FSim.Model.Xini[5];

// Форматируем строку для Memo1

S := Format('%-10d %-10.4f %-10.4f',

[CurRev,FSim.Model.State[1].AsFloat, RelIncl]);

// Выводим строку в Memo1 и в файл результатов

Memo1.Lines.Add(S);

Write(FOut, CurRev:5);

for k := 1 to 4 do

Write(FOut, FSim.Model.State[k].AsFloat:10:3);

Write(FOut, RelIncl:10:3);

Writeln(FOut);

end;

end;

procedure TForm1.OnStopSim(Sender:TObject; var Stop:boolean);

// Обработчик события симулятора OnStop

begin

// Флаг FCancel = true, если пользователь нажал кнопку Cancel

// в процессе моделирования

Stop := FCancel;

if Stop then

Memo1.Lines.Add('Моделирование прервано пользователем');

end;

procedure TForm1.bRunClick(Sender: TObject);

// Обработчик нажатия кнопки «Поехали»

var

M : TOrbitModel;// Ссылка на мат. модель

R : TFloat; // Начальный безразмерный радиус

V : TFloat; // Начальная безразмерная скорость

Incl : TFloat; // Начальное наклонение

N : integer; // Число витков перелета

begin

//Устанавливаем исходное состояние кнопок

bCancel.Enabled := false;

bRun.Enabled := true;

//Считываем индекс текущего метода из TComboBox

FMethodIndex := cbMethod.ItemIndex;

// Создаем объект-симулятор и объект-модель

FSim := TSimulator.Create;

M := TOrbitModel.Create;

// Выбираем метод интегрирования

case FMethodIndex of

0: FSim.Method := TEulerCauchy.Create;

1: FSim.Method := TRungeKutta4.Create;

end;

FSim.Model := M; // Передаем модель симулятору

// Считываем начальные условия из компонент TEdit

R := StrToFloat(edRadius.Text);

Incl := StrToFloat(edInclination.Text)*utToRad;

V := 1/Sqrt(R);

M.Ini.AssignItems([R,0,V,0,Incl,0,0]);// Начальные условия

// Номинальное ускорение в Control

M.Control.Anom := StrToFloat(edAccelerat.Text);

N := StrToInt(edRevol.Text);// Число витков

FOrbSteps := StrToInt(edOrbitSteps.Text);//Шагов на витке

// Присваиваем ссылки на обработчики событий симулятора

FSim.OnEnter := OnEnterSim;

FSim.OnOutput := OnOutputSim;

FSim.OnExit := OnExitSim;

FSim.OnStop := OnStopSim;

// Начальное время и шаг интегрирования

FSim.IniTime := 0;

FSim.Step := TwoPi/FOrbSteps;

// Блокируем кнопку Run и активируем кнопку Cancel

bCancel.Enabled := true;

bRun.Enabled := false;

// Запускаем процесс моделирования

FSim.SysTime := N*TwoPi;

// Уничтожаем симулятор

FSim.Free;

// Восстанавливаем исходное состояние кнопок

bRun.Enabled := true;

bCancel.Enabled := false;

end;

procedure TForm1.bCancelClick(Sender: TObject);

// Обработчик события - нажатия на кнопку Cancel

begin

FCancel := true;

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

// Задаем метод интегрирования по умолчанию

cbMethod.ItemIndex :=0;

end;

end.