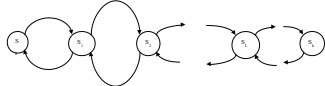
7 . Многоканальная смо с отказами |m|m|k|0|.

S₀ – система не занята

S₁ - в системе одна заявка

S₂ - в системе 2 заявки

S_k - в системе к заявок, все каналы заняты

2

Случайные процессы, которые имеют граф такого вида, называются процессами гибели и размножения.

Составим уравнения для предельных вероятностей состояния:

;

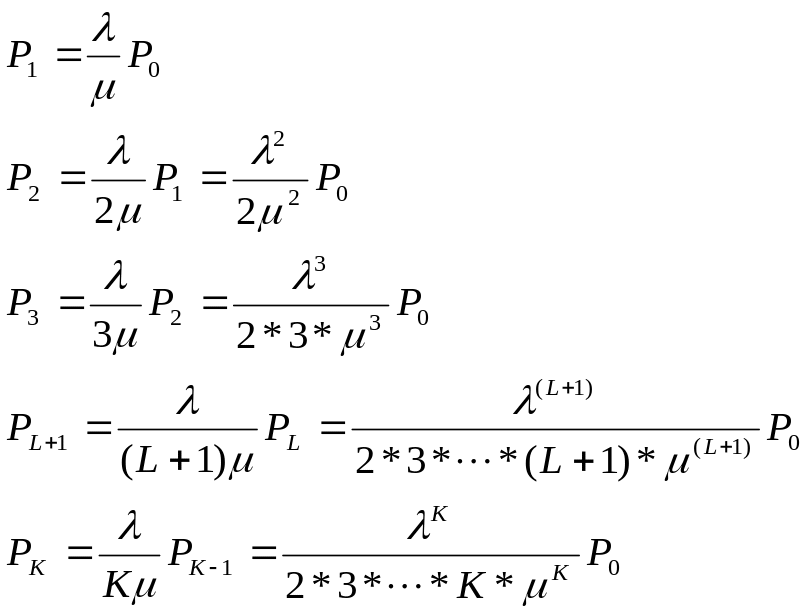
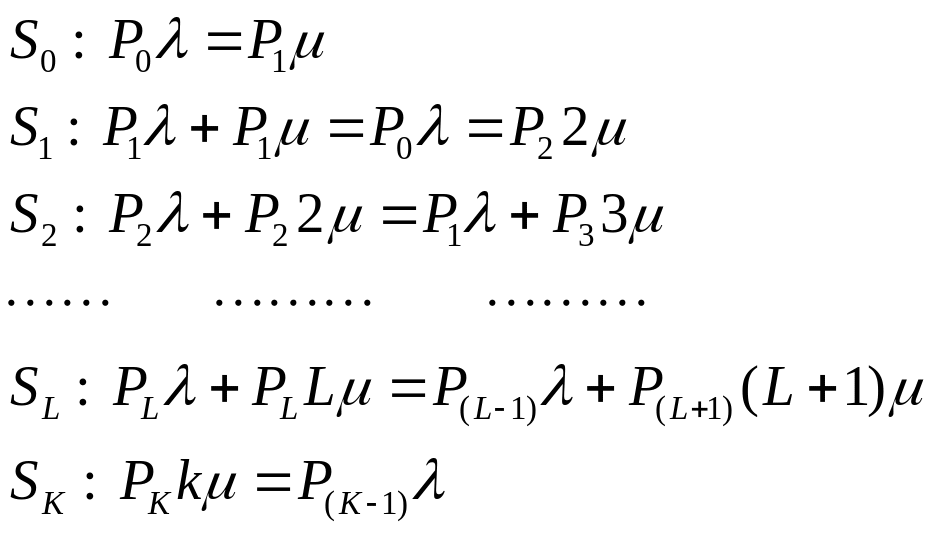
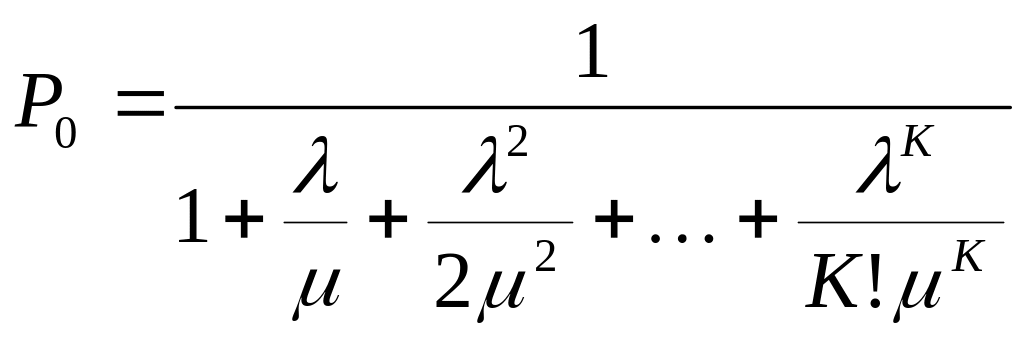
Обозначим (приведённая интенсивность входного потока). Физический смысл заключается в том, что она показывает, сколько заявок поступит на вход СМО за время обслуживания одной заявки.

_//**

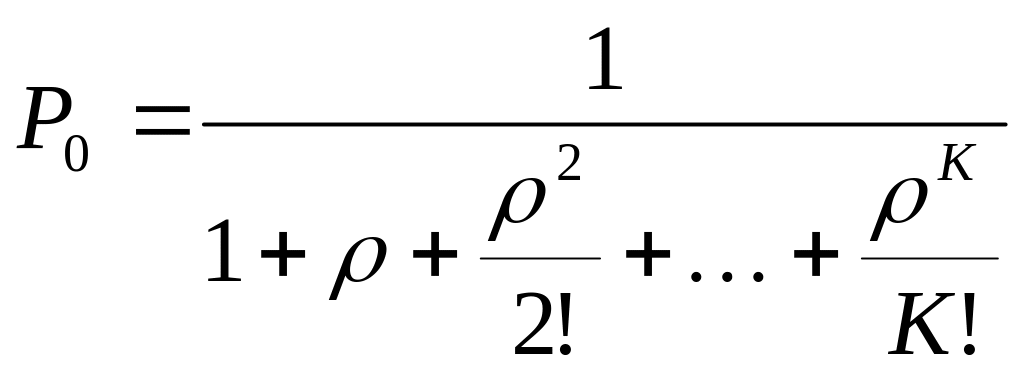Заметим: полученные формулы для предельных вероятностей состояний этой СМО называют формулами Эрланга.

q и всегда дополняют друг друга до единицы (т. к. система в смысле пропускной способности, либо пропускает, либо отказывает)

; - среднее число занятых каналов

можно определить как мат.ожидание дискретной случайной величины

, но проще определить таким способом: один постоянно занятый канал обслуживает заявок, а, если занято каналов, то она обслуживает заявок.

;

Многоканальная СМО нужна, что понизить вероятность отказа и повысить производительность.

8. Одноканальная смо с ограниченной длинной очереди.

/ М / М / 1 / n /

- состояние, когда в системе нет ни одной заявки

- когда в системе одна заявка (канал занят, очередь пуста)

- когда в системе две заявки(одна в канале, одна в очереди)

…………………………………………………………

- (n+1)-заявка ( всё занято)

-?(ср. длина очереди); m-?; -?(ср. вр. ожид-я в очереди): -?(ср. вр. пребывания заявки в системе)

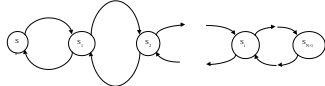
Составить ур-я для каждого состояния и из них получить вероятности состояний

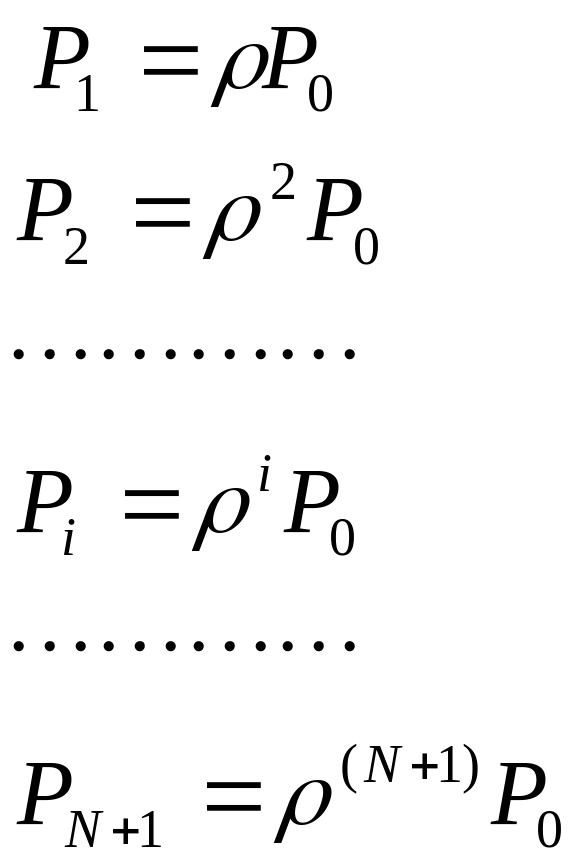
При N=1,

При

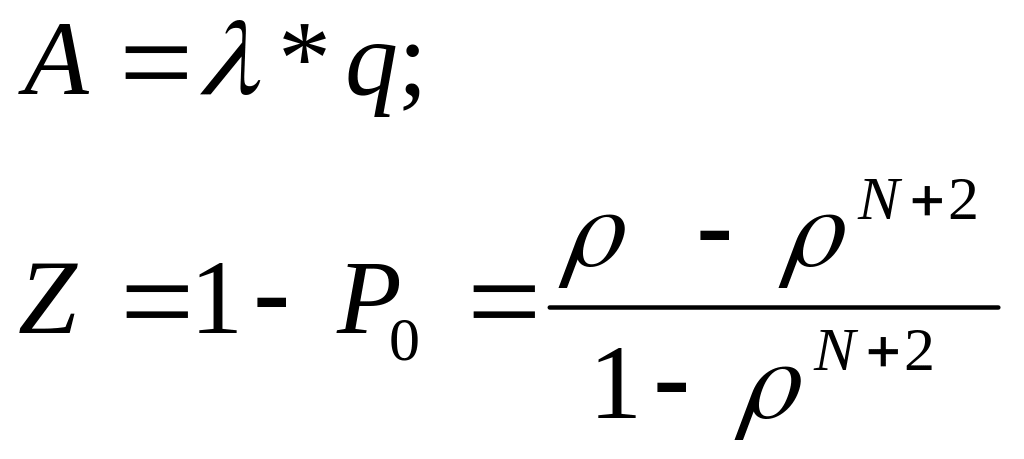
Z=1- P₃=1- ⁿ⁺²)=( ⁿ⁺¹)/(1- ⁿ⁺²) //**

_с= ⁿ⁺²)

P₂+2P₃+...+nP_n+1

Определим ν как математическое ожидание случайной и дискретной величины.

Т. к. одна заявка будет находиться в очереди с вероятностью Р₂₁, вторая заявка с вероятностью P₃ и т.д.

ν=1ρ² P₀+2ρ³P₀+…+nρⁿ⁺¹ P₀=ρ²P₀(1+2ρ+3ρ²+...+nρ^n-1)=ρ²P₀Y (*)

∑ρ=ρ+ρ²+ρ³+...+ρⁿ=(ρ-ρⁿ⁺¹)/(1-ρ)

1+2ρ+3ρ²+...+nρ^n-1=(∑ρ)’

(∑ρ)’=([1-(n+1)ρⁿ](1-ρ)+ρ-ρⁿ⁺¹)/(1-ρ²)= (1-(n+1)ρⁿ-ρ+(n+1) ρⁿ⁺¹⁺ρ-ρⁿ⁺¹)/(1-ρ²)=

=(1-(n+1)ρⁿ+nρⁿ⁺¹)/(1-ρ²)=Y

Следующая величина числа заявок находящиеся в системе равной сумме случайных величин числа заявок, находятся в очереди и число заявок находящиеся на обслуживание, тогда на основе теоремы о сумме математических ожиданий.

m=ν+j

где j – среднее число заявок, находится на обслуживании.

j= 0P₀+1(1-P₀)=1- P₀=(ρ-ρⁿ⁺²)/(1-ρⁿ⁺²)

Z=j=ē=1- P₀

λ_вых=Z*μ

m= ρ²* P₀Y+(ρ-ρⁿ⁺²)/(1-ρⁿ⁺²)

Если промежуточная заявка застанет систему свободной, то t_от≠0, если система в состоянии S₁, т. е. канал занят, а очередь свободна, то t_от=1/μ, если S₂, то t_от=2τ и т.д.

t_от=τP₁+2τP₂+3τP₃+...+nτP_n=(1/μ)ρP₀+(2/μ)ρ²P₀+(3/μ)ρ³P₀+...+(n/μ)ρⁿP₀=

=ρP₀/μ(1+2ρ+3ρ²+...+nρ^n-1)= (ρP₀/μ)Y

t_от=ν/ρμ=ν/λ

Время ответа t_пр=t_ож+t_обр=t_ож+q/μ=t_ож+qτ

t_пр=m/λ для всех систем массового обслуживания, которые можно описать аналитически.