3. Потоки событий. Простейший поток.

Это последовательность событий, след. Одно за другим. Если какая-то система переходит одного состояния в др., то удобнее эти переходы рассматривать под влиянием каких-то событий. Если события следуют через опред. интервалы времени, то поток называется регулярным. Гораздо чаще встречаются потоки со случайными интервалами времени между событиями.

Простейший поток.

Поток событий называется простейшим, если он обладает 3 свойствами:

1. Стационарности;

2. Отсутствием последствий;

3. Ординарности.

Поток называется стационарным, если число событий, которые происходят за интервал времени, зависит от интервала времени и не зависит от положения интервала на временной оси. Т.е. однородность потока по времени.

Поток событий называется потоком без последствия если для любых не пересекающихся интервалов времени число событий, которые попадают на один из них, не зависит от того, сколько попало на другие.

Поток называется ординарным, если вероятность того, что за элементарный промежуток времени вероятность появления 2-х событии пренебрежительна мала по сравнению с вероятностью появления одиночного события.

Простейший поток событий обычно называется Пуассоновский.

Если поток удовлетворяет условиям (2), (3), но не (1) то он наз нестационарным Пуассоновским.

За время τ появится m событий с вероятностью: P_m=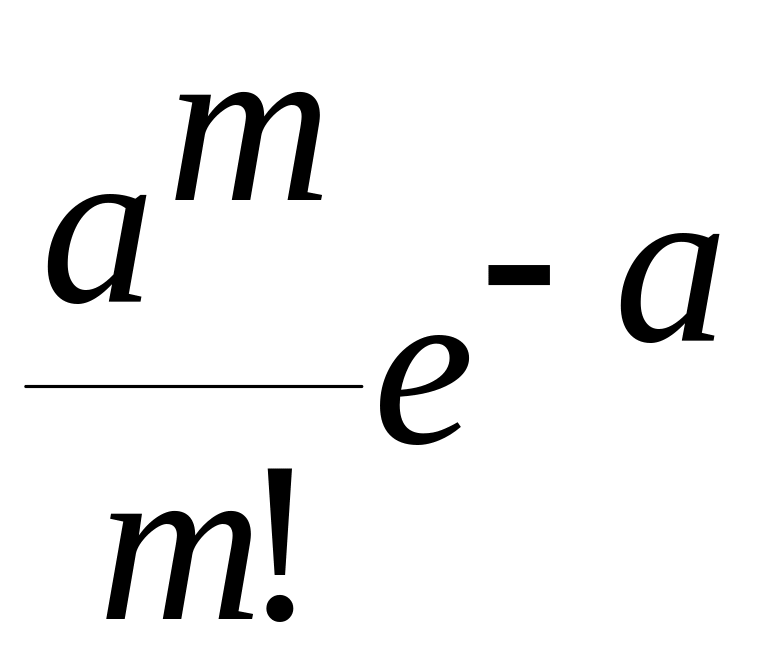 (1)

1. среднее число событий, котор. Происходят за интервал τ .

Для простейшего потока: . Удобнее характеризовать интервалами времени между событиями. Очевидно, что в простейшем случае это случайная величина.

Определим закон распределения случайной величины:

F(t)-?

F(t)=P(T<t)

Определим функцию распределения через вероятность того, что за время t произойдет хотя бы одно событие. Вероятность определим через вероятность противоположного события.

F(t)=1-P₀

Из (1):

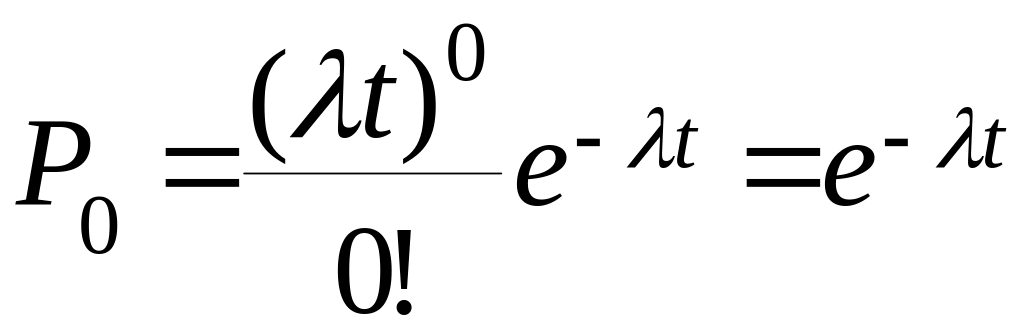
f(t)=F’(t)= - экспоненциальный закон распределения. (2)

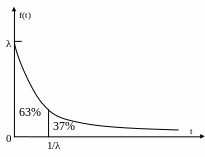
m_t –мат. ожидание;

m_t=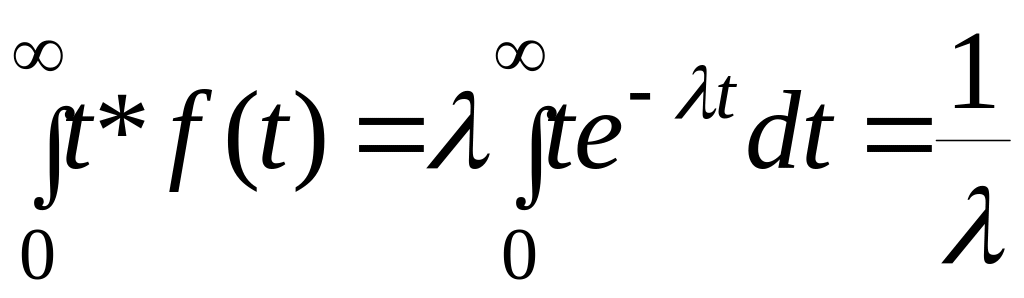

D_t=

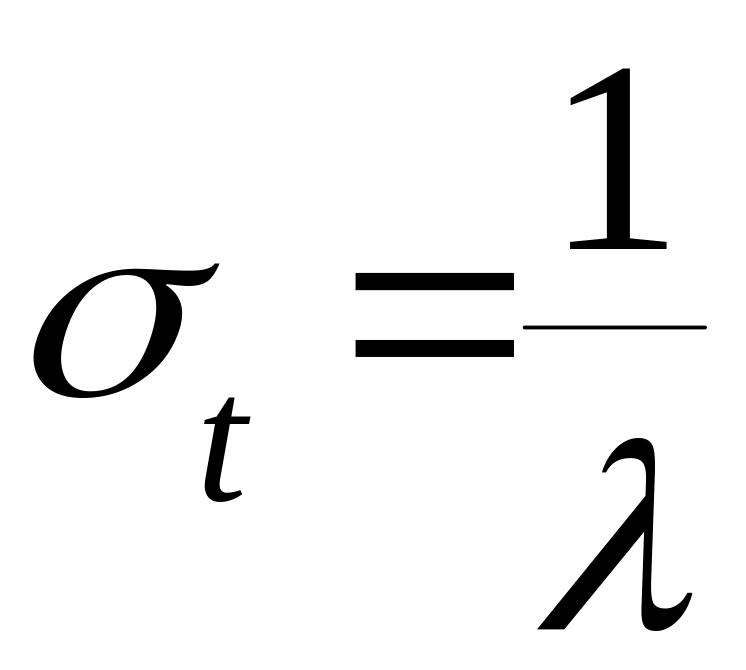
Т.е. при экспоненциальном законе число коротких интервалов (меньших, чем мат. ожидание) существенно больше, чем длинных.

Тот факт, что m_t и σ_t равны можно использовать как критерий степени близости реального потока к экспоненциальному.

Если случайная величина времени между соседними событиями распределяется по экспоненциальному закону, то можно утверждать, что поток событий простейший (и наоборот!).

Простейший поток является универсальным в том смысле, что если суммировать несколько ординарных и стационарных потоков, то результирующий получится простейшим.

Определим “элемент вероятности появления события” -за ∆t произойдет 1 событие: P₁(∆t)-? Т.к. поток ординарный, то

P₁(∆t) 1- P₀(∆t)

P₀(∆t)= =/разложим в ряд/=1-(1-λ∆t) λ∆t

4. Потоки Эрланга.

Потоки Эрланга получаются из простейших потоков в результате их “просеивания”.

Пример: если в простейшем потоке пропускать 1 событие, а учитывать каждое 2-ое, то в результате получится поток Эрланга 2-ого порядка.

Очевидно, что СВ времени в потоке Эрланга k-ого порядка = сумме k СВ в исходном простейшем потоке.

T=T₁+T₂+…+T_k

Найдем закон распределения СВ.

О пределим вероятность того, что следующее событие произойдет в интервале dt. Это может произойти при свершении следующих событий:

от t₀ до ∆t в исходном простейшем потоке произойдет (k-1) событие, а на ∆t одно k-ое событие.

P_k-1(t)=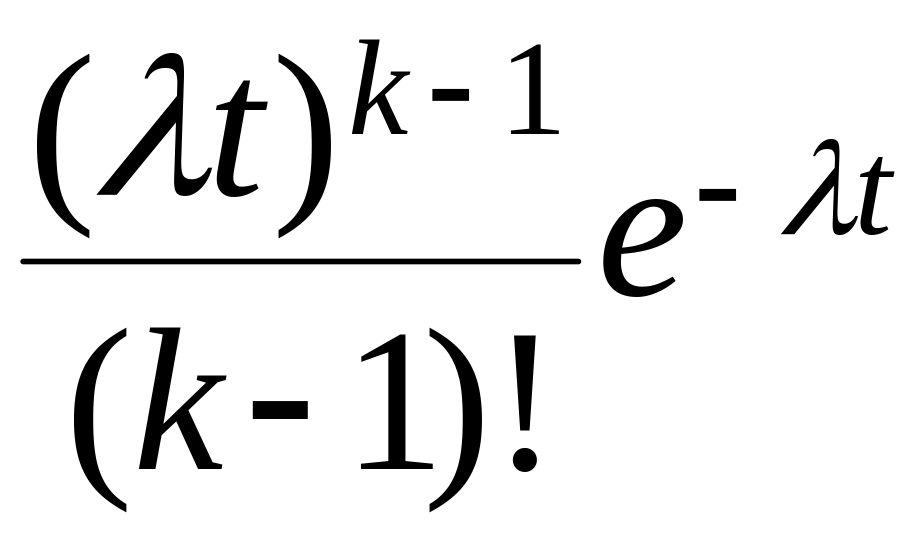

λ –среднее число событий, в исходном простейшем потоке за ед. времени.

P₁(dt) λdt

f_k(t)dt=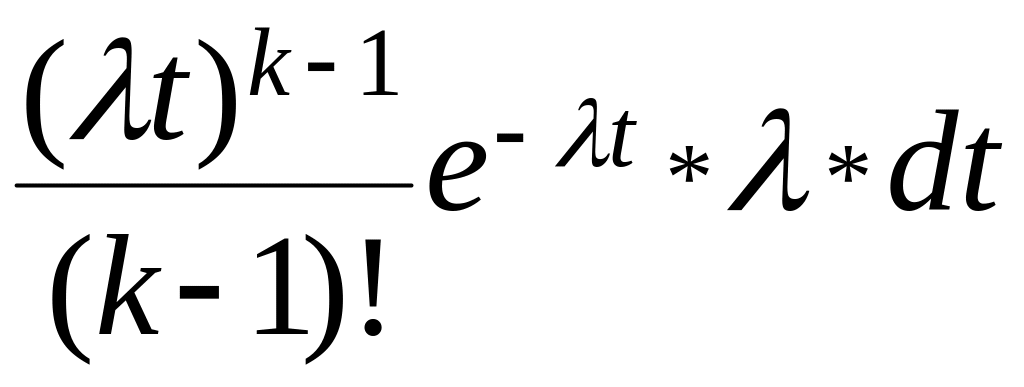

f_k(t) =

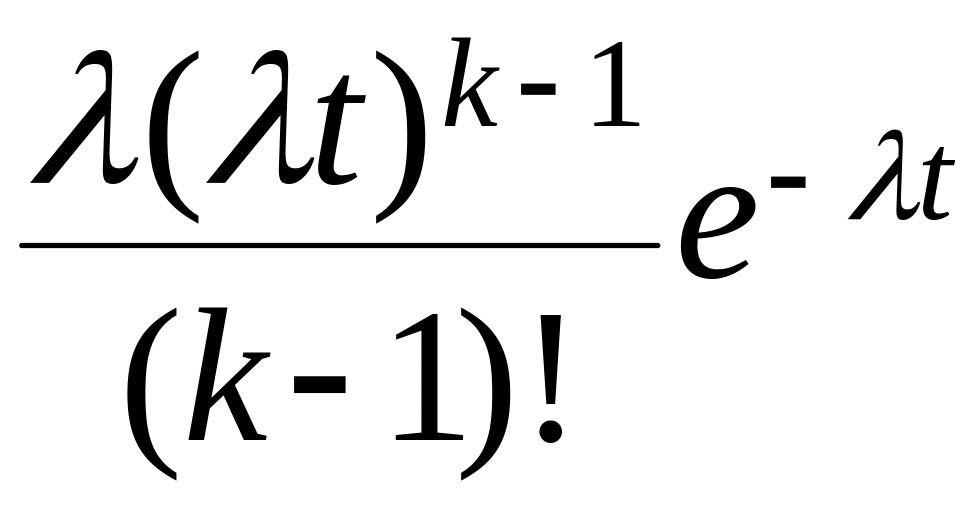
По теореме сложения мат. ожиданий и дисперсий:

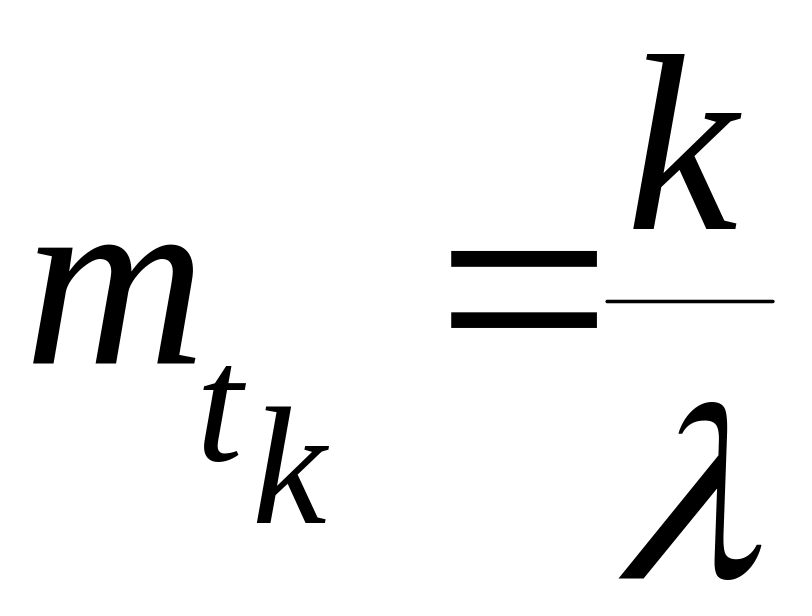
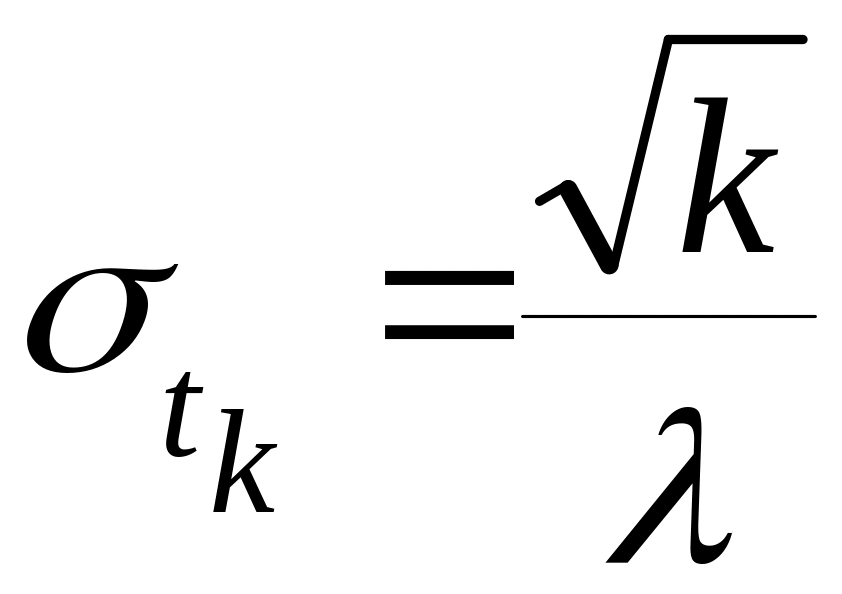
В полученных выражениях фигурирует параметр λ, т.е. параметр исходного простейшего потока. Выразим эти значения через параметр самого потока Эрланга:

Λ_k – среднее число событий в единицу времени в потоке Эрланга k-го порядка, т.е. это интенсивность событий в потоке Эрланга k-го порядка.

- подставим в закон Эрланга:

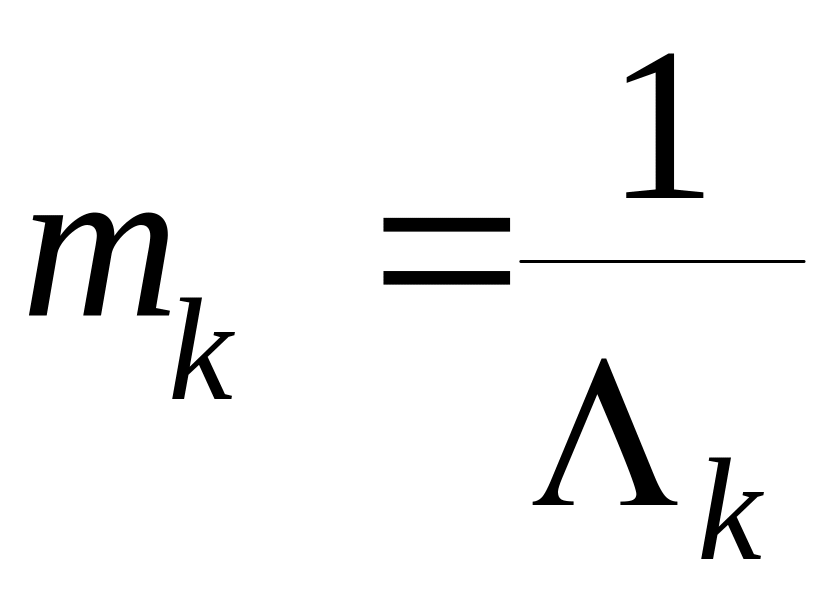
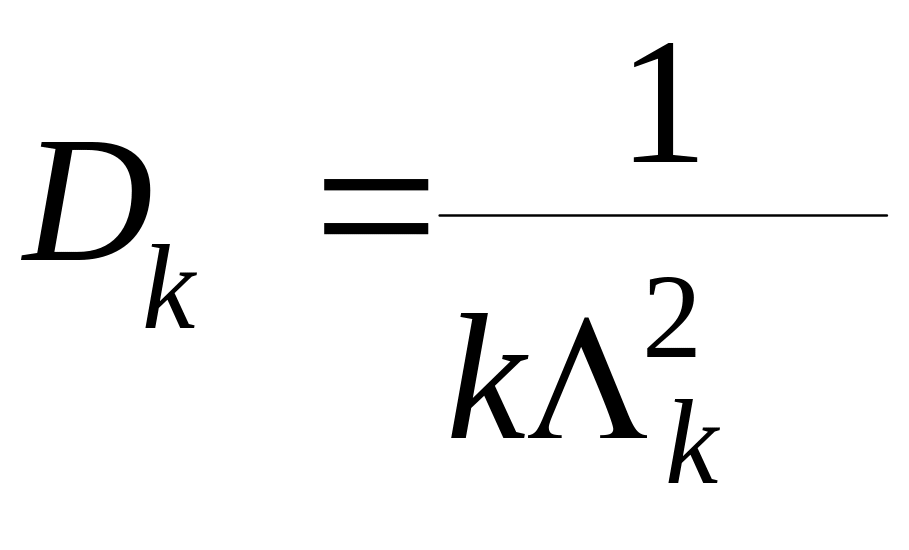
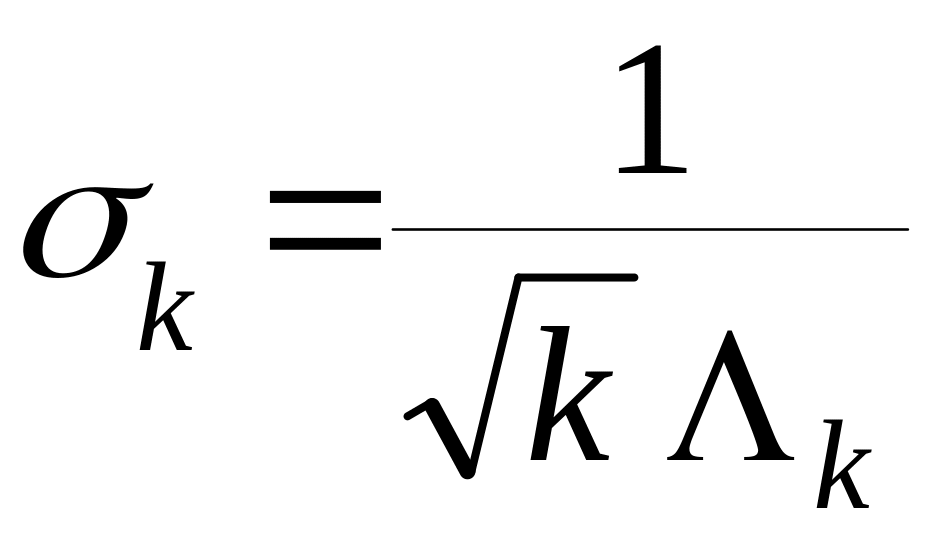
Если устремить k→ ∞, при этом m_k оставить неизменным, то характеристики разброса стремятся к нулю, т.е. поток приближается к регулярному. Иначе говоря, изменяя k, с помощью потоков Эрланга можно перекрыть весь диапазон потоков в смысле наличия или отсутствия свойства последействия, т.е. от полного отсутствия до жесткой функциональной зависимости.