1. Понятие марковских случайных процессов
Если объект переходит случайным образом из одного состояния в другое, то говорят, что в нем развивается случайный процесс.
Случайный процесс называется марковским, если для каждого момента t=t0 вероятность любого состояния системы в будущем, т.е. при t>t0 зависит только от состояния этой системы в настоящий момент времени, т.е. при t=t0 и не зависит от того, когда и каким путем система приняла это состояние. Т.е. в Марковском случайном процессе (МСП) развитие не зависит от прошлого этого процесса, а зависит только от настоящего. Назовем его процессом без предыстории или без последействия.
Существует несколько классов МСП.
МСП называется процессом с дискретными состояниями, если эти состояния можно перечислить, пронумеровать, если переход из одного состояния в другое происходит скачкообразно.
МСП называется непрерывным, если переход из одного состояния в другое происходит плавно.
МСП называется процессом с дискретным временем, если переход из одного состояния в другое осуществляется в строго определенные, фиксированные моменты времени.
МСП называется случайным процессом с непрерывным временем, если переход осуществляется в произвольные моменты времени.
Мы будем рассматривать дискретные МСП с непрерывным временем.
2.Дискретный мсп с непрерывным временем. Вероятности состояний. Уравнение Колмогорова.
Пусть задан НМСП, он может принимать n состояний:
S1, S2,…, Sn.
Последовательность этих состояний называют марковской цепью.
МСП удобно характеризовать вероятностью состояний Pi(t).
Введем понятие плотности
вероятности перехода из состояния Si
в состояние Sj
и обозначим ее как
.
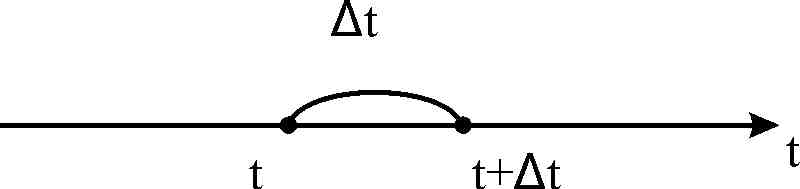
При малых значениях
с точностью до бесконечно малых величин
высших порядков
Если
не зависит от времени, то марковский
процесс называется однородным, если
зависит, то неоднородным.
Определение вероятностей состояний.
Н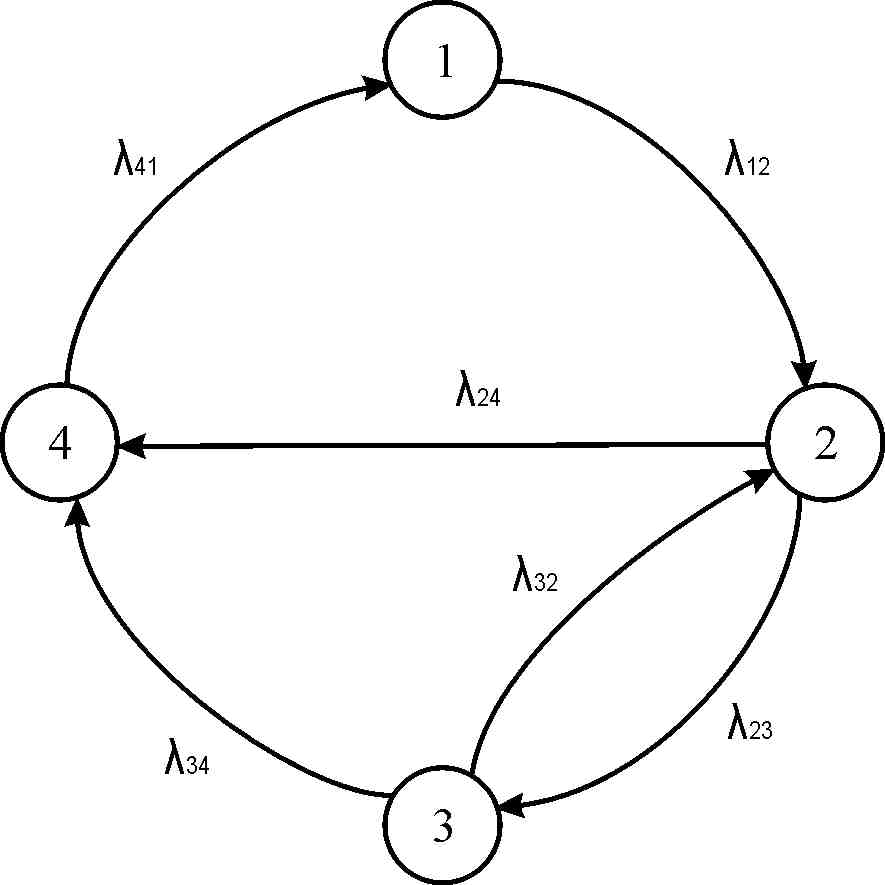
МСП
удобно представлять в виде направленного
графа.
Пример:
4 состояния: S1, S2, S3 , S4.
Возможны переходы:
P1(t)=?
(вероятность того, что система находится в состоянии S1 во время t)
Проанализируем развитие процесса. Система будет в состоянии S1 в двух случаях:
1. Если система в момент времени t находилась в состоянии S4 и за перешла в состояние S1.
2. Если в система в момент времени t находилась в состоянии S1 и за не перешла в S2.
Определим вероятности:
1
)
условная вероятность перехода
2) 
Переходя к пределам и приравнивая к 0 получим:
Определим P2(t):
1) Если система в S1 и перешла за в S2
2) Если система в S3 и перешла за в S2
3) Если система в S2 и не перешла за ни в S3, ни в S4.
1) 
2) 
Делая преобразования, получим:
Эти уравнения называются уравнения Колмогорова. Решая их, можно определить вероятность любого состояния НМСП.
При t=0 P2=1, P1=P3=P4=0 {0, 1, 0, 0}
Уравнения легко записать по механическому правилу:
В левой части производная от соответствующего состояния по времени, правая часть содержит столько членов, сколько стрелок связано с этим состоянием. Каждый член равен произведению вероятности того состояния из которого он выходит на соответствующую плотность вероятности перехода. Каждый член со знаком "+", если стрелка входит в состояние, и "-", если выходит.
Это правило справедливо для всех МСП с непрерывным временем.
Для получения уравнений для предельных вероятностей состояний надо производные в уравнение Колмагорова приравнять к нулю.
S1: 0= λ41P’4(t)- λ12P1(t)
Механическое правило
Сумма членов, соотв. выходным стрелкам равна сумме членов соотв. входным стрелкам. А каждый член равен произведению вероятностных состояний на плотность вероятности перехода.
Каждая из этих вероятностных состояний физически означает среднюю относительную долю времени, в течении которого система находится в данном состоянии.