28. Знакочередующиеся ряды. Теорема Лейбница
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
Пусть для знакочередующегося ряда
выполняются следующие условия:
(монотонное
убывание {an})
.
Тогда этот ряд сходится.
29. Знакопеременные ряды. Абсолютная и условная сходимость
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Знакочередующиеся ряды являются частным случаем знакопеременных рядов.
Ряд 
называется абсолютно
сходящимся, если ряд 
также
сходится.
Если ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется условно
сходящимся, если сам он сходится, а ряд,
составленный из модулей его членов,
расходится.
30. Функциональные ряды
Рассмотрим
ряд, 
,
членами которого являются функции,
определенные на промежутке 
.
При каждом фиксированном 
имеем
числовой ряд, сходимость которого может
быть исследована рассмотренными ранее
методами. Сумма функционального
ряда
также
является функцией от х: 
.
По определению предела последовательности:
если для 
можно
указать номер 
(
что интересно, для каждого фиксированного
- свой номер, т.е. 
),
такой, что для 
выполняется
неравенство 
,
то это и означает, что функциональный
ряд сходится к функции
.
Множество 
,
для которого это выполняется, называется
областью сходимости функционального
ряда.
Равномерная
сходимость функционального ряда.
Пусть
,
т.е. функциональный ряд сходится. Если
для
можно
указать номер
независимо
от 
,
такой, что для
выполняется
неравенство
,
то говорят, что функциональный ряд
сходится равномерно на множестве .
Исследование
на равномерную сходимость. Признак
Вейерштрасса равномерной сходимости
функционального ряда: если существует
сходящийся числовой ряд 
с
положительными членами, такой, что для
всех 
,
начиная с некоторого номера и
всех
выполняется
неравенство
,
то функциональный ряд
сходится
на
равномерно.
Числовой ряд
в
этом случае называют мажорантой для
функционального ряда.
31. Степенные ряды. Интервал сходимости
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
в
котором коэффициенты 
берутся
из некоторого кольца 
.
Рассмотрим
функцию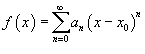 
.
Ее областью определения является
множество тех значений x, при которых
ряд сходится. Область определения такой
функции называется интервалом
сходимости.
32. Ряды Тейлора и Маклорена
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если
приведенное разложение сходится в
некотором интервале x, т.е. 
,
то оно называется рядом Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a = 0, то
такое разложение называется рядом
Маклорена:
Разложение некоторых функций в ряд Маклорена
