
- •Кинематика
- •Модели в механике
- •2.Кинематическое описание движения
- •4.Перемещение. Скорость. Вычисление пройденного пути
- •6. Плоское вращение. Угловая скорость и ускорение. Связь между векторами скорости и угловой скорости.
- •Динамика материальной точки
- •1.Основная задача механики. Законы Ньютона
- •2. Система единиц си. Границы применимости классической механики
- •3. Импульс. Закон сохранения импульса системы материальных точек. Применение закона сохранения импульса к абсолютно неупругому удару. Движение тел с переменной массой.
- •4.Момент импульса. Момент силы. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса.
- •5. Силы в природе. Четыре вида взаимодействия. Силы сухого и вязкого трения
- •6. Упругая сила.Закон Гука. Деформация тела
- •7. Энергия. Работа. Мощность. Кинетическия энергия
- •8. Консервативные и неконсервативные силы. Потенциальная энергия
- •9. Закон сохранения энергии в механике
- •10. Применение з-ов сохранения к абсолютно упругому удару
- •11.Закон всемирного тяготения. Движение в центральном поле. Космические скорости. Законы Кеплера
- •Динамика абсолютно твёрдого тела
- •Вращение абсолютно твёрдого тела вокруг неподвижной оси и его кинетическая энергия
- •3.Момент инерции тела и его физический смысл. Пример вычисления момента инерции твёрдого тела. Теорема Штейнера Согласно определению момент инерции твёрдого тела равен
- •Момент инерции тела относительно нецентральной оси Теорема Штейнера
- •6. Гироскоп. Угловая скорость прецессии
- •Колебания
- •1.Уравнения гармонических колебаний и его основные параметры
- •2..Колебания груза под действием упругой сил. Энергия гармонических колебаний
- •Математический и физич маятники
- •4.Уранение затухающих гармонических колебаний. Декремент затухания, добротность.
- •5.Вынужденные колебания. Резонанс
- •6.Сложение гармонических колебаний одинаковой частоты и направления. Векторная диаграмма
- •7. Сложение гармонических колебаний различной частоты. Биения
- •8. Сложение гармонических колебаний одинаковой частоты и взаимно перпендикулярного направления . Фигуры Лиссажу.
- •1.Волновые процессы. Продольные и поперечные волны
- •2.Уравнение плоской гармонической волны и её основный параметры. Фазовая скорость. Волновой пакет. Групповая скорость
- •3.Волновое уравнение
- •4.Фазовая скорость волны в твёрдых телах
- •5. Скорость звука в газах
- •6. Энергия упругой волны. Вектор Умова. Громкость звука
- •7. Стоячие волны. Колебания струны.
- •8. Эффект Доплера для акустических волн
- •Мкт газов
- •1.Статистический и термодинамический методы исследования. Опытные законы идеального газа. Уравнение Клайперона-менделеева
- •2,Основное уравнение молекулярно – кинетической теории газов.
- •Молекулярно-кинетический смысл температуры
- •3,Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекул газа. Внутренняя энергия идеального газа
- •4.Распределение Максвелла. Средняя, среднеквадратичная и наиболее вероятная скорости газовых молекул.Максвелловское распределение молекул по их скоростям и энергиям
- •5 Барометрическая формула. Распределение Больцмана
- •6.Среднее число столкновений и средняя длина свободного пробега молекул
- •7. Явление переноса в термодинамическинеравноверстных системах. Тепло-проводимость. Диффузия. Вязкость
- •Термодинамика
- •1.Внутренняя энергия системы. Работа и теплота
- •2.Первое начало термодинамики. Графическое изображение термодинамических процессов и работы
- •3.Теплоёмкость вещества. Уравнение Майера
- •4.Адиабатный и политропный процессы идеального газа
- •5.Классическая теория теплоёмкостей идеального газа и её трудности. Квантомеханическое объяснение
- •6,Круговой процесс(цикл) Обратимые и необратимые процессы
- •7.Энтропия , её статистическое толкование и связь с термодинамической вероятностью
- •8,Второе начало термодинамики
- •9. Тепловые двигатели и холодильные машины. Цикл карно. Теорема Карно
- •Реальные газы, жидкости и твёрдые тела
- •1.Силы и потенциальная энергия межмолекулярного взаимодействия
- •2. Уравнение Ван-дер-Ваальса
- •3.Изотермы Ван-дер-Ваальса и их анализ. Критические состояния
- •4. Внутренняя энергия реального газа
- •5.Фазовые переходы 1и 11 рода. Диаграмма состояния. Тройная точка. Уравнение Клайперона-Клаузиуса
- •6.Свойчтва жидкостей. Поверхностное напряжение
- •7. Твёрдые тела. Типы кристаллических твёрдых тел
6. Гироскоп. Угловая скорость прецессии
Гироскопом
(или волчком) наз-я массивное симметричное
тело, вр-ся с большой скоростью вокруг
оси симметрии. Эту ось будем называть
осью гироскопа. Ось гироскопа является
одной из главных осей инерции. Поэтому,
если она не поворачивается в пространстве,
момент импульса равен
 ,
где I
–момент инерции относительно оси
гироскопа.При попытке вызвать поворот
оси гироскопа наблюдается своеобразное
явление, получившее название
гироскопического
эффекта:под
действием сил, которые, казалось бы,
должны вызвать поворот оси гироскопа
ОО
вокруг прямой
,
где I
–момент инерции относительно оси
гироскопа.При попытке вызвать поворот
оси гироскопа наблюдается своеобразное
явление, получившее название
гироскопического
эффекта:под
действием сил, которые, казалось бы,
должны вызвать поворот оси гироскопа
ОО
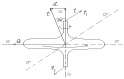
вокруг прямой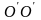 (см.
рисунок), ось гироскопа поворачивается
вокруг прямой О''О''
направленной вдоль направления действия
сил
(см.
рисунок), ось гироскопа поворачивается
вокруг прямой О''О''
направленной вдоль направления действия
сил
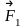 и
и
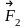 . Поведение гироскопа
. Поведение гироскопа
о
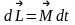 ,
которое имеет такое же направление, как
и
.
Спустя время dtмомент
импульса гироскопа
,
которое имеет такое же направление, как
и
.
Спустя время dtмомент
импульса гироскопа
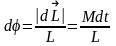 ,Отсюда
следует, что поворот оси гироскопа в
новое положение произошел с угловой
скоростью
,Отсюда
следует, что поворот оси гироскопа в
новое положение произошел с угловой
скоростью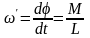 .Перепишем
это соотношение в виде:
.Перепишем
это соотношение в виде:
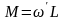 Векторы
,
и
Векторы
,
и
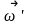 взаимно перпендикулярны (вектор
направлен
вдоль прямой О’’О’’,
на нас). Поэтому связь между ними можно
записать в векторном виде :
взаимно перпендикулярны (вектор
направлен
вдоль прямой О’’О’’,
на нас). Поэтому связь между ними можно
записать в векторном виде :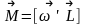 .Заметим, что эта формула справедлива
лишь в том случае, если ’
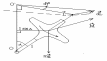
<<Допустим,
что ось гироскопа может свободно
поворачивается вокруг некоторой точки
О
(см. рисунок). Р
.Заметим, что эта формула справедлива
лишь в том случае, если ’
<<Допустим,
что ось гироскопа может свободно
поворачивается вокруг некоторой точки
О
(см. рисунок). Р
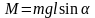 ,
где m-
масса гироскопа, l-
расстояние от точки О
до центра инерции гироскопа,
,
где m-
масса гироскопа, l-
расстояние от точки О
до центра инерции гироскопа,
 - угол, образованный осью гироскопа с
вертикалью.Под действием момента сил
момент импульса
получит
за время dt
приращение
,
перпен-е вектору
.
При этом вертик-я плоскость, прох-я ч/з
ось гироскопа, повернётся на угол
- угол, образованный осью гироскопа с
вертикалью.Под действием момента сил
момент импульса
получит
за время dt
приращение
,
перпен-е вектору
.
При этом вертик-я плоскость, прох-я ч/з
ось гироскопа, повернётся на угол
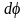 .
Угол
при этом не меняется. Таким образом, в
поле сил тяжести ось гироскопа с
неподвижной точкой О
поворачивается вокруг вертикали,
описывая конус. Такое движение гир-па
наз-я прецессиейУгл-
скорость прец’
можно найти,
.
Угол
при этом не меняется. Таким образом, в
поле сил тяжести ось гироскопа с
неподвижной точкой О
поворачивается вокруг вертикали,
описывая конус. Такое движение гир-па
наз-я прецессиейУгл-
скорость прец’
можно найти,
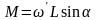 .
Подставляем сюда M
получим
.
Подставляем сюда M
получим
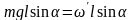 , отсюда
, отсюда - угловая скорость
прецессии.
- угловая скорость
прецессии.
Колебания
1.Уравнения гармонических колебаний и его основные параметры
Колебания, при которых колеблющаяся величина изменяется со временем по закону косинуса или синуса, называются гармоническими колебаниями.
Таким
образом, движение системы, находящейся
под действием силы вида
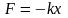 ,
представляет собой гармоническое
колебание.
,
представляет собой гармоническое
колебание.
Параметры гармонического колебания:
А – амплитуда, т.е. максимальное смещение от положения равновесия;
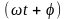 -
фаза колебаний, которая измеряется в
радианах;
-
фаза колебаний, которая измеряется в
радианах;
-
начальная фаза, т.е. фаза в момент времени
 ;
;
T - период колебаний, т.е. время одного полного колебания;
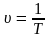 -
частота колебаний, т.е. число колебаний
в единицу времени. (измеряется в герцах,
-
частота колебаний, т.е. число колебаний
в единицу времени. (измеряется в герцах,
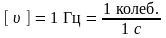 ).
).
Поскольку
косинус – функция периодическая с
периодом
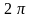 ,
то
,
то
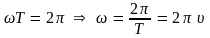 -
циклическая частота.
-
циклическая частота.
В случае колеблющегося шарика, подвешенного на пружине:
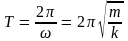
Продифференцировав x(t) по времени, получим выражение для скорости:
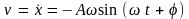 ,
,
а,
продифференцировав еще раз, найдем
выражение для ускорения:
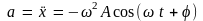
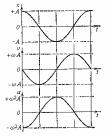
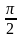 ,
а ускорение а и
смещение х
находятся в противофазе.
,
а ускорение а и
смещение х
находятся в противофазе.
На рисунке сопоставлены графики для смещения, скорости и ускорения.
