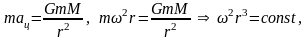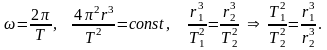- •Кинематика
- •Модели в механике
- •2.Кинематическое описание движения
- •4.Перемещение. Скорость. Вычисление пройденного пути
- •6. Плоское вращение. Угловая скорость и ускорение. Связь между векторами скорости и угловой скорости.
- •Динамика материальной точки
- •1.Основная задача механики. Законы Ньютона
- •2. Система единиц си. Границы применимости классической механики
- •3. Импульс. Закон сохранения импульса системы материальных точек. Применение закона сохранения импульса к абсолютно неупругому удару. Движение тел с переменной массой.
- •4.Момент импульса. Момент силы. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса.
- •5. Силы в природе. Четыре вида взаимодействия. Силы сухого и вязкого трения
- •6. Упругая сила.Закон Гука. Деформация тела
- •7. Энергия. Работа. Мощность. Кинетическия энергия
- •8. Консервативные и неконсервативные силы. Потенциальная энергия
- •9. Закон сохранения энергии в механике
- •10. Применение з-ов сохранения к абсолютно упругому удару
- •11.Закон всемирного тяготения. Движение в центральном поле. Космические скорости. Законы Кеплера
- •Динамика абсолютно твёрдого тела
- •Вращение абсолютно твёрдого тела вокруг неподвижной оси и его кинетическая энергия
- •3.Момент инерции тела и его физический смысл. Пример вычисления момента инерции твёрдого тела. Теорема Штейнера Согласно определению момент инерции твёрдого тела равен
- •Момент инерции тела относительно нецентральной оси Теорема Штейнера
- •6. Гироскоп. Угловая скорость прецессии
- •Колебания
- •1.Уравнения гармонических колебаний и его основные параметры
- •2..Колебания груза под действием упругой сил. Энергия гармонических колебаний
- •Математический и физич маятники
- •4.Уранение затухающих гармонических колебаний. Декремент затухания, добротность.
- •5.Вынужденные колебания. Резонанс
- •6.Сложение гармонических колебаний одинаковой частоты и направления. Векторная диаграмма
- •7. Сложение гармонических колебаний различной частоты. Биения
- •8. Сложение гармонических колебаний одинаковой частоты и взаимно перпендикулярного направления . Фигуры Лиссажу.
- •1.Волновые процессы. Продольные и поперечные волны
- •2.Уравнение плоской гармонической волны и её основный параметры. Фазовая скорость. Волновой пакет. Групповая скорость
- •3.Волновое уравнение
- •4.Фазовая скорость волны в твёрдых телах
- •5. Скорость звука в газах
- •6. Энергия упругой волны. Вектор Умова. Громкость звука
- •7. Стоячие волны. Колебания струны.
- •8. Эффект Доплера для акустических волн
- •Мкт газов
- •1.Статистический и термодинамический методы исследования. Опытные законы идеального газа. Уравнение Клайперона-менделеева
- •2,Основное уравнение молекулярно – кинетической теории газов.
- •Молекулярно-кинетический смысл температуры
- •3,Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекул газа. Внутренняя энергия идеального газа
- •4.Распределение Максвелла. Средняя, среднеквадратичная и наиболее вероятная скорости газовых молекул.Максвелловское распределение молекул по их скоростям и энергиям
- •5 Барометрическая формула. Распределение Больцмана
- •6.Среднее число столкновений и средняя длина свободного пробега молекул
- •7. Явление переноса в термодинамическинеравноверстных системах. Тепло-проводимость. Диффузия. Вязкость
- •Термодинамика
- •1.Внутренняя энергия системы. Работа и теплота
- •2.Первое начало термодинамики. Графическое изображение термодинамических процессов и работы
- •3.Теплоёмкость вещества. Уравнение Майера
- •4.Адиабатный и политропный процессы идеального газа
- •5.Классическая теория теплоёмкостей идеального газа и её трудности. Квантомеханическое объяснение
- •6,Круговой процесс(цикл) Обратимые и необратимые процессы
- •7.Энтропия , её статистическое толкование и связь с термодинамической вероятностью
- •8,Второе начало термодинамики
- •9. Тепловые двигатели и холодильные машины. Цикл карно. Теорема Карно
- •Реальные газы, жидкости и твёрдые тела
- •1.Силы и потенциальная энергия межмолекулярного взаимодействия
- •2. Уравнение Ван-дер-Ваальса
- •3.Изотермы Ван-дер-Ваальса и их анализ. Критические состояния
- •4. Внутренняя энергия реального газа
- •5.Фазовые переходы 1и 11 рода. Диаграмма состояния. Тройная точка. Уравнение Клайперона-Клаузиуса
- •6.Свойчтва жидкостей. Поверхностное напряжение
- •7. Твёрдые тела. Типы кристаллических твёрдых тел
9. Закон сохранения энергии в механике
Рассм-м
сист-у, сост-ю из nмат-ых
точек, м/у кот-и действуют конс-ые силы
внутреннего взаимод-ия
,
и кроме того на мат-ыет.действуют внешние
консервативные силы
и внешние неконсервативные силы
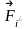 Для
каждой материальной точки запишем
второй закон Ньютона:
Для
каждой материальной точки запишем
второй закон Ньютона: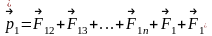 ,
,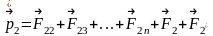 ,
,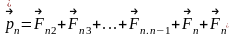 .Далее
левые и правые части каждого уравнения
умножим скалярно на
.Далее
левые и правые части каждого уравнения
умножим скалярно на
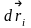 ,
соответственно, где
,
соответственно, где
 – номер материальной точки. Покажем
это на примере
-ой
материальной точки:
– номер материальной точки. Покажем
это на примере
-ой
материальной точки: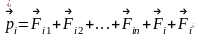
,
,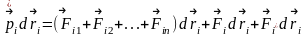 .Это
равенство можно записать в виде:
.Это
равенство можно записать в виде: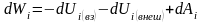 ,или
,или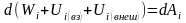 ,где
,где
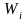 – кинетическая энергия
-ой
материальной точки,
– кинетическая энергия
-ой
материальной точки,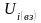 – внутренняя потенциальная энергия
-ой
материальной точки,
– внутренняя потенциальная энергия
-ой
материальной точки,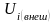 – внешняя потенциальная энергия
-ой
материальной точки,
– внешняя потенциальная энергия
-ой
материальной точки,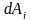 – работа, которую совершают над
-ой
материальной точкой внешняя неконсервативная
сила.Просуммируем левые и правые части
преобразованных указанным образом
уравнений движения.
– работа, которую совершают над
-ой
материальной точкой внешняя неконсервативная
сила.Просуммируем левые и правые части
преобразованных указанным образом
уравнений движения.
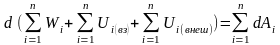 ,
или
,
или
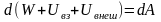 ,где
– кинетическая энергия системы
материальных точек,
,где
– кинетическая энергия системы
материальных точек,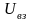 ,
,
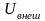 – внутренняя и внешняя потенциальная
энергия м.т.,
– внутренняя и внешняя потенциальная
энергия м.т.,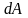 – полная работа внешних неконсервативных
сил.Если внешние нек-е силы отсутствуют,
правая часть полученного уравнения
будет равна нулю и, следовательно, полная
механическая энергия системы остается
постоянной:
– полная работа внешних неконсервативных
сил.Если внешние нек-е силы отсутствуют,
правая часть полученного уравнения
будет равна нулю и, следовательно, полная
механическая энергия системы остается
постоянной: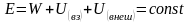 - закон
сохранения механической энергии системы
материальных точек.Полная
механическая энергия системы м.т, на
которые действуют лишь консервативные
силы, остается постоянной, т.е. сохраняется
во времени.Для
замкнутой системы з-н сох-я полной
механической энергии имеет вид:
- закон
сохранения механической энергии системы
материальных точек.Полная
механическая энергия системы м.т, на
которые действуют лишь консервативные
силы, остается постоянной, т.е. сохраняется
во времени.Для
замкнутой системы з-н сох-я полной
механической энергии имеет вид: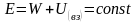 Полная
мех-я энергия замкнутой системы
материальных точек, между которыми
действуют только консервативные силы,
остается постоянной, т.е. сохраняется
во времени.Если
в замкнутой системе, кроме консерв-х,
действуют такие неконсервативные силы,
например, силы трения, то полная
механическая энергия системы не
сохраняется.
Полная
мех-я энергия замкнутой системы
материальных точек, между которыми
действуют только консервативные силы,
остается постоянной, т.е. сохраняется
во времени.Если
в замкнутой системе, кроме консерв-х,
действуют такие неконсервативные силы,
например, силы трения, то полная
механическая энергия системы не
сохраняется.
10. Применение з-ов сохранения к абсолютно упругому удару
Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).
Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса.
Обозначим скорости шаров массами m1 и m2 до удара через ν1 и ν2, после удара - через ν1' и ν2' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.
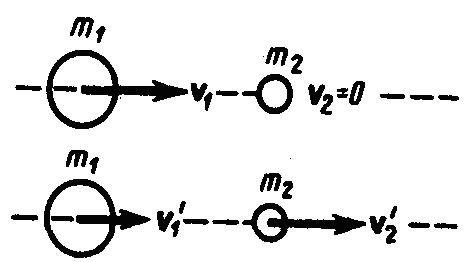
Рис.1
При указанных допущениях законы сохранения имеют вид
![]() (1)
(1)
![]() (2)
(2)
Произведя соответствующие преобразования в выражениях (1) и (2), получим
![]() (3)
(3)
![]() 4)
4)
откуда![]() (5)
(5)
Решая уравнения (3) и (5), находим
![]() (6)
(6)
![]() (7)
(7)
11.Закон всемирного тяготения. Движение в центральном поле. Космические скорости. Законы Кеплера
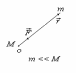
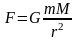 - з-н всем-го тяг-я,гдеG=
6.67
- з-н всем-го тяг-я,гдеG=
6.67 Нм2/кг2
- - гравит- постоянная.
Нм2/кг2
- - гравит- постоянная.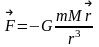 -сила
грав-гопритяжения.Гравита-е
взаим-е осуществляется ч/з грав-е
поле.1)Грав-ная сила – консервативная
сила
-сила
грав-гопритяжения.Гравита-е
взаим-е осуществляется ч/з грав-е
поле.1)Грав-ная сила – консервативная
сила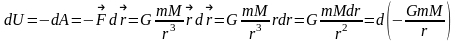 ,
,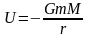 - потенциальная энергия
гравитационного поля.Имеет
место з-н сох-я мех-ой эн-ии телE
= W
+ U
= const2)Гравитационная
сила – центральная сила:
Возьмем мом--т импульса
- потенциальная энергия
гравитационного поля.Имеет
место з-н сох-я мех-ой эн-ии телE
= W
+ U
= const2)Гравитационная
сила – центральная сила:
Возьмем мом--т импульса
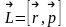 и расс-им з-н изменен его во времени:
и расс-им з-н изменен его во времени:
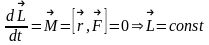 з-н
сохраненмомента импульса тела.Поск-ку
момент импульса тела сохр-ся, дв-е тела
происходит в одной плоскости.Прист
теперь к расс-нию движения тела:
з-н
сохраненмомента импульса тела.Поск-ку
момент импульса тела сохр-ся, дв-е тела
происходит в одной плоскости.Прист
теперь к расс-нию движения тела:
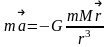 Удобно
перейти к системе отсчета, кот-я связана
с
и вращается с угл-й ск-ю
.(
Удобно
перейти к системе отсчета, кот-я связана
с
и вращается с угл-й ск-ю
.(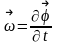 -угловая
скоростьВовращ-я сист-е отсчета надо
добавить центр-ю силу, поэтому ур-е (1)
примет вид:
-угловая
скоростьВовращ-я сист-е отсчета надо
добавить центр-ю силу, поэтому ур-е (1)
примет вид: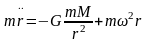 ур-е
д-я во вращ-сясист отсчета.Вычислим
ур-е
д-я во вращ-сясист отсчета.Вычислим
 :
: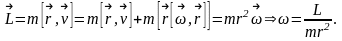 Здесь
использована ф-ла раскрытия дв-го
век-гопроиз-ия
Здесь
использована ф-ла раскрытия дв-го
век-гопроиз-ия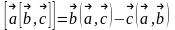 Тогда
(2) примет вид
Тогда
(2) примет вид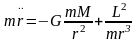 Перейдем
к полярной системе координат и выразимr
как функцию угла
Перейдем
к полярной системе координат и выразимr
как функцию угла
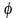 ,
т.е.
,
т.е.
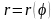 .
Можно показать, что решение уравнения
(3) может быть представлено следующим
образом:
.
Можно показать, что решение уравнения
(3) может быть представлено следующим
образом:
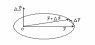
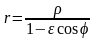 траектория
движения тела в полярных координ-хгде
траектория
движения тела в полярных координ-хгде
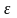 - эксцентриситет,
- эксцентриситет,
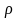 - параметр, опр-ий размеры траектории.Возможны
4 типа траекторий:1)
- параметр, опр-ий размеры траектории.Возможны
4 типа траекторий:1)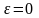 - окружность;2)
- окружность;2) - эллипс;3)
- эллипс;3)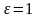 - парабола;4)
- парабола;4)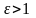 - гип-ла.Рассмотримкач-но характер дв-я
с помощью потенциальной кривой. Для
этого введем пот-ю эн-ю центр
- гип-ла.Рассмотримкач-но характер дв-я
с помощью потенциальной кривой. Для
этого введем пот-ю эн-ю центр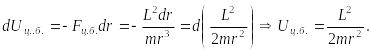
 обежной
силы:Тогда во вращающейся системе
отсчета:
обежной
силы:Тогда во вращающейся системе
отсчета: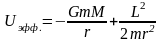 -эффективная
потенциальная энергия.
-эффективная
потенциальная энергия.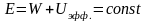 за-н
со-я эн-и.Посмотрим,от
каких физических величин зависит
эксцент-т орбиты
и параметр
.
Вернемся к неподвижной системе
отсчета.
,
за-н
со-я эн-и.Посмотрим,от
каких физических величин зависит
эксцент-т орбиты
и параметр
.
Вернемся к неподвижной системе
отсчета.
,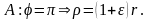
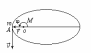 Используем
з-ы сохранения энергии и момента
импульса.Для точки А
Используем
з-ы сохранения энергии и момента
импульса.Для точки А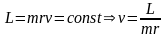
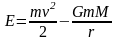 =con
=con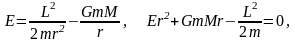
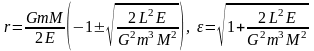 эксцентр-т
орб-ы.
эксцентр-т
орб-ы.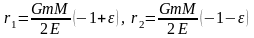 -малая
и большая полуоси
-малая
и большая полуоси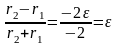 действительно
эксцентриситет эллипсаподстав.
и
действительно
эксцентриситет эллипсаподстав.
и
 в (5), получ
в (5), получ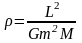 параметр
орбиты
Из
ф-ы (6) получим энергию E:
параметр
орбиты
Из
ф-ы (6) получим энергию E: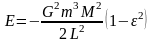 - полная механ-ая энергия телаВведем в
точке Aускор-е
своб-гопад-я g:
- полная механ-ая энергия телаВведем в
точке Aускор-е
своб-гопад-я g:
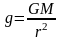 .Тогда
.Тогда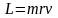 ,
,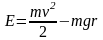 ПодставLиEв6)и(7),получим
ПодставLиEв6)и(7),получим
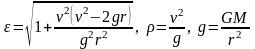 ускорение
свободного падения в точке A.
ускорение
свободного падения в точке A.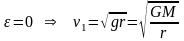 1-я
космическая скорость
1-я
космическая скорость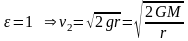 2-якосмическая
скорость.З-ы
Кеп-ра1) Все планеты
движутся по эллиптич-м орбитам, причем
Солнце нах-ся в одном из фокусов орбиты.
2)Отрезок, соедин-й Солнце с планетой,
опис-т равные площади за равные пром-и
времени. 3)Квадр-ы периодов обращения
неск-х планет вокруг Солн относ-я, как
кубы больших полуосей эллипсов.1)Мы
показ-и, что замкнутые орбиты явл-я
эллипсами.2)2-й
закон Кеплера представлсобой закон
сохр-я момента имп-а.
2-якосмическая
скорость.З-ы
Кеп-ра1) Все планеты
движутся по эллиптич-м орбитам, причем
Солнце нах-ся в одном из фокусов орбиты.
2)Отрезок, соедин-й Солнце с планетой,
опис-т равные площади за равные пром-и
времени. 3)Квадр-ы периодов обращения
неск-х планет вокруг Солн относ-я, как
кубы больших полуосей эллипсов.1)Мы
показ-и, что замкнутые орбиты явл-я
эллипсами.2)2-й
закон Кеплера представлсобой закон
сохр-я момента имп-а.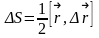 вектор
площади Треуг-а.
вектор
площади Треуг-а.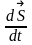 секторальная
площадь.
секторальная
площадь.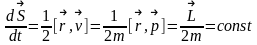 3)
Для эллипсов вывод более громоздкий,
но для круговых орбит просто:
3)
Для эллипсов вывод более громоздкий,
но для круговых орбит просто: