6. Упругая сила.Закон Гука. Деформация тела

. Абсолютно упругий удар: столкновение двух тел, в результате которого в обоих взаимодействующих телах не остаётся никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения энергии.

Абсолютно неупругий удар: столкновение двух тел, в результате которого тела объединившись, двигаются дальше как единое целое.

(например шары из пластелина)

В данном случае закон сохранения энергии не соблюдается. Вследствии деформации происходит потеря кинетической энергии, перешедшей в другие формы энергии. Эту потерю можно определить по разности кинетической энергии тело до и после удара.

или (учтено выражение для v)

Если ударяемое тело было первоначально неподвижно, то ;

Если m2>>m1 ,то v<<v1 и почти вся кинетическая энергия при ударе переходит в другие виды энергии.

7. Энергия. Работа. Мощность. Кинетическия энергия

Энергия- универсальная мера различных форм движения и взаимодействия.

Работа силы:количественная характеристика процесса обмена энергией между взаимодействующими телами.

Элементарная работа силы: (где альфа-угол между векторами F и dr; ds=/dr/- элементарный путь; Fs – проекция вектора F на вектор dr).Работа силы на участке 1-2 и определяется площадью заштрихованной фигуры.Работа – скалярная величина.Мощность: физическая величина, характеризующая скорость совершения работы. ( N=dA/dt )За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени (N=Fdr/dt=Fv) т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка.Мощность – скалярная величина.Единицы работы: Дж (1 Дж – это работа, совершаемая силой 1Н на пути 1м: 1 Дж=1Н м)Единицы мощности: Вт (1 Вт – это мощность, при которой за время 1 с совершается работа 1 Дж: 1Вт=1Дж/с)Кинетическая энергия(или энергия движения) определяется массами и скоростями рассматриваемых тел. Рассмотрим материальную точку, движущуюся под действием силы . Работа этой силы увеличивает кинетическую энергию материальной точки . Вычислим в этом случае малое приращение (дифференциал) кинетической энергии:

При вычислении использован второй закон Ньютона , а также - модуль скорости материальной точки. Тогда можно представить в виде: - кинетическая энергия движущейся материальной точки.Умножив и разделив это выражение на , и учитывая, что , получим 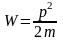связь между импульсом и кинетической энергией движущейся материальной точки

8. Консервативные и неконсервативные силы. Потенциальная энергия

Консервативные силы: сила, работа которой при перемещении тела из одного положения в другое не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положения тела. (например гравитационные силы, кулоновские)Все другие силы (например силы трения) относятся к неконсервативным силамПотенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела. Мы видели, что работу силы тяжести при криволинейном движении материальной точки можно представить в виде разности значений функции , взятых в точке 1 и в точке 2: .

Оказывается, что всегда, когда силы консервативны, работу этих сил на пути 1 2 можно представить в виде: .Функция , которая зависит только от положения тела – называется потенциальной энергией.Тогда для элементарной работы получим – работа равна убыли потенциальной энергии.

Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.Величину , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:

– полная механическая энергия тела.В заключении заметим, что используя второй закон Ньютона , дифференциал кинетической энергии можно представить в виде:

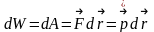.Дифференциал потенциальной энергии , как указывали выше, равен: .

Таким образом, если сила – консервативная сила и отсутствуют другие внешние силы, то , т.е. в этом случае полная механическая энергия тела сохраняется.