2. Система единиц си. Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)

При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.

Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

3. Импульс. Закон сохранения импульса системы материальных точек. Применение закона сохранения импульса к абсолютно неупругому удару. Движение тел с переменной массой.

Рассмотрим систему, состоящую из n материальных точек. Между материальными точками действуют силы внутреннего взаимодействия , а также на материальные точки действуют внешние силы . Здесь - внутренняя сила, действующая на i-ю материальную точку со стороны k-й материальной точки, - внешняя сила, действующая на i-ю материальную точку.Материальные точки системы обладают импульсом: - импульс i-ой материальной точки.Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующая равна нулю: = 0. Запишем для каждой материальной точки второй закон Ньютона: , ,… .

Просуммировав левые и правые части этих уравнений, получим

.Сумма производных равна производной от суммы, а также по третьему закону Ньютона: . В результате получим: .Если система материальных точек замкнута, т.е. , тогд = 0, и имеет место закон сохранения импульса: закон сохранения импульса системы материальных точек.

Если система материальных точек является замкнутой, то суммарный импульс системы остаётся постоянным, т.е. сохраняется во времени.

Уравнение движения тела с переменной массой

На выполнении закона сохранения импульса основано движение ракеты, если её рассматривать как замкнутую систему. Мы рассмотрим более общий случай движения тела с переменной массой при наличии внешней силы, например, движение ракеты в гравитационном поле Земли.

Для этого рассмотрим два близких момента времени t и t+ dt и вычислим измение импульса системы: ракета + вытекающий газ.Пусть в момент времени t импульс системы равен .

За время dt выброшен газ массой dm со скоростью относительно ракеты, и импульса системы: ракета + газ стал равен:

.

В выражении для раскроем скобки и пренебрежем малой величиной более высокого порядка ( )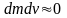

.

Тогда изменение импульса системы: ракета + газ за время dt равно:

, .

Подставляя это во второй закон Ньютона , получим уравнение движения тела с переменной масой - уравнение Мещерского.Второй член справа в этом уравнении представляет собой - силу реактивной тяги, где — секундный расход топлива.