4.Уранение затухающих гармонических колебаний. Декремент затухания, добротность.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления пропорциональна величине скорости: ,где R – постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила 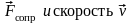имеют противоположные направления; следовательно, их проекции на ось х имеют разные знаки.Второй закон Ньютона при наличии сил сопротивления имеет вид: Применив обозначения:

получим: (4)ДУ затухающих гармонических колебаний.

Отметим, что представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при R = 0). Эту частоту называют собственной частотойсистемы.При не слишком сильном затухании (при < ) общее решение ур-я (4) имеет вид: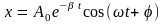 ,(5)

где A₀и произвольные постоянные, величина, определяемая формулой . На рисунке дан график функции (5). Пунктирными линиями показаны пределы, в кот-х нах-я смещение колеблющейся точки х.Всоот-и с видом ф-ии (5) движение системы можно рассматривать как гармоническое колебание частоты с амплитудой, изм-ся по закону:

.Верхняя из пунктирных кривых дает график функции A(t), причем величина представляет собой амплитуду в начальный момент времени.Скорость затухания колебаний определяется величиной , которую называют коэффициентом затухания.Период затухания колебаний равен: (6) При незначительном сопротивлении среды ( ) период колебаний практически не изменяется и равен 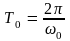. Последующие наибольшие отклонения в какую–либо сторону (например, и т.д. на рис.) образуют геометрическую прогрессию. Действительно, если , то , и т.д.Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно: Это соотношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания. 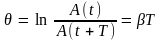Для характеристики колебательной системы обычно используется логарифмический декремент затухания . Выразив в соответствии с (7) через и , можно закон убывания амплитуды со временем записать в виде: .

Дляхарактеристики колебательной системы часто употребляется также величина , называемая добротностьюколебательной системы. Ранее мы установили, что полная энергия колеблющейся системы пропорциональна квадрату амплитуды. В соответствии с этим энергия системы при затухающих колебаниях уб-т со временем по закону: ,где - значение энергии при .Из формулы периода затухающих колебаний (6) следует, что с ростом коэф-а зат-я период колебаний увеличивается. При 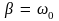период колебаний обращается в бесконечность, т.е. движение перестает быть периодическим.При решение дифференциального уравнения (5) оказывается равным сумме двух экспонент: , где и 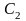- постоянные, значения которых зависят от начальных условий (от и ), , .Д в-е в этом случае носит апериодический (непериодический) характер – выведенная из положения рав-я сист-а возвр-я в положение равн-я, не совершая колебаний. Н а рис показано 2 возможных спос-ба возв-я системы к пол-юрав-я при апериодическом движении. Каким из этих способов приходит система к положению равновесия, зависит от начальных условий.