
- •Кинематика
- •Модели в механике
- •2.Кинематическое описание движения
- •4.Перемещение. Скорость. Вычисление пройденного пути
- •6. Плоское вращение. Угловая скорость и ускорение. Связь между векторами скорости и угловой скорости.
- •Динамика материальной точки
- •1.Основная задача механики. Законы Ньютона
- •2. Система единиц си. Границы применимости классической механики
- •3. Импульс. Закон сохранения импульса системы материальных точек. Применение закона сохранения импульса к абсолютно неупругому удару. Движение тел с переменной массой.
- •4.Момент импульса. Момент силы. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса.
- •5. Силы в природе. Четыре вида взаимодействия. Силы сухого и вязкого трения
- •6. Упругая сила.Закон Гука. Деформация тела
- •7. Энергия. Работа. Мощность. Кинетическия энергия
- •8. Консервативные и неконсервативные силы. Потенциальная энергия
- •9. Закон сохранения энергии в механике
- •10. Применение з-ов сохранения к абсолютно упругому удару
- •11.Закон всемирного тяготения. Движение в центральном поле. Космические скорости. Законы Кеплера
- •Динамика абсолютно твёрдого тела
- •Вращение абсолютно твёрдого тела вокруг неподвижной оси и его кинетическая энергия
- •3.Момент инерции тела и его физический смысл. Пример вычисления момента инерции твёрдого тела. Теорема Штейнера Согласно определению момент инерции твёрдого тела равен
- •Момент инерции тела относительно нецентральной оси Теорема Штейнера
- •6. Гироскоп. Угловая скорость прецессии
- •Колебания
- •1.Уравнения гармонических колебаний и его основные параметры
- •2..Колебания груза под действием упругой сил. Энергия гармонических колебаний
- •Математический и физич маятники
- •4.Уранение затухающих гармонических колебаний. Декремент затухания, добротность.
- •5.Вынужденные колебания. Резонанс
- •6.Сложение гармонических колебаний одинаковой частоты и направления. Векторная диаграмма
- •7. Сложение гармонических колебаний различной частоты. Биения
- •8. Сложение гармонических колебаний одинаковой частоты и взаимно перпендикулярного направления . Фигуры Лиссажу.
- •1.Волновые процессы. Продольные и поперечные волны
- •2.Уравнение плоской гармонической волны и её основный параметры. Фазовая скорость. Волновой пакет. Групповая скорость
- •3.Волновое уравнение
- •4.Фазовая скорость волны в твёрдых телах
- •5. Скорость звука в газах
- •6. Энергия упругой волны. Вектор Умова. Громкость звука
- •7. Стоячие волны. Колебания струны.
- •8. Эффект Доплера для акустических волн
- •Мкт газов
- •1.Статистический и термодинамический методы исследования. Опытные законы идеального газа. Уравнение Клайперона-менделеева
- •2,Основное уравнение молекулярно – кинетической теории газов.
- •Молекулярно-кинетический смысл температуры
- •3,Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекул газа. Внутренняя энергия идеального газа
- •4.Распределение Максвелла. Средняя, среднеквадратичная и наиболее вероятная скорости газовых молекул.Максвелловское распределение молекул по их скоростям и энергиям
- •5 Барометрическая формула. Распределение Больцмана
- •6.Среднее число столкновений и средняя длина свободного пробега молекул
- •7. Явление переноса в термодинамическинеравноверстных системах. Тепло-проводимость. Диффузия. Вязкость
- •Термодинамика
- •1.Внутренняя энергия системы. Работа и теплота
- •2.Первое начало термодинамики. Графическое изображение термодинамических процессов и работы
- •3.Теплоёмкость вещества. Уравнение Майера
- •4.Адиабатный и политропный процессы идеального газа
- •5.Классическая теория теплоёмкостей идеального газа и её трудности. Квантомеханическое объяснение
- •6,Круговой процесс(цикл) Обратимые и необратимые процессы
- •7.Энтропия , её статистическое толкование и связь с термодинамической вероятностью
- •8,Второе начало термодинамики
- •9. Тепловые двигатели и холодильные машины. Цикл карно. Теорема Карно
- •Реальные газы, жидкости и твёрдые тела
- •1.Силы и потенциальная энергия межмолекулярного взаимодействия
- •2. Уравнение Ван-дер-Ваальса
- •3.Изотермы Ван-дер-Ваальса и их анализ. Критические состояния
- •4. Внутренняя энергия реального газа
- •5.Фазовые переходы 1и 11 рода. Диаграмма состояния. Тройная точка. Уравнение Клайперона-Клаузиуса
- •6.Свойчтва жидкостей. Поверхностное напряжение
- •7. Твёрдые тела. Типы кристаллических твёрдых тел
Кинематика
Модели в механике
Классичмехан или механика Ньютона изучдвиж-е тел, кот сост в перемещении тел или их частей друг относительно друга. Механику можно разделить на два раздела: кинематику и динамику. Кинематикаизучает движение тел, не интересуясь причинами, обуславливающими это движение. Динамикаизучает движение тел в связи с теми причинами ( взаимодействиями между телами), которые обуславливают тот или иной характер движения.Если мы собираемся изучить движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение. Кроме того, для описания движения необходимо также определять время. Это делается с помощью часов.Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета.Для того, чтобы получить возможность описывать движение количественно, приходится связывать с телами, образующими систему отсчета, какую-либо (например, декартову)систему координат.
2.Кинематическое описание движения
Мат-я точка – это тело, размерами которого в условиях данной задачи можно пренебречь. Материальная точка при своем движении описывает некоторую линию, которая называется траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение.
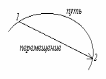
Перемещение - это прямолинейный отрезок, проведенный из точки 1 в точку 2.
Существуют три способа описания движения материальной точки: координатный, векторный и естественный.

Если с системой отсчета связать декартову систему координат (X, Y, Z) , то положение материальной точки А можно задать с помощью координат (x, y, z). Траекторию движения мы определим, если будем знать функцию x(t), y(t), z(t).
Векторыйспособ:
В
этом случае дост-о выбрать в систотсч
точку Онач
отсчета. Полож-е точки А
будет опр-ся вектором
 ,
провед из начала отсчета в данную точку
А.
Этот вектор
наз-я
радиус –
вектором
т.А.
Траект-я движ-я будет опр-ся ф-ей
(t).
Для того, чтобы установить связь между
этими двумя способами описания, введем
три единичных вектора, орты
,
провед из начала отсчета в данную точку
А.
Этот вектор
наз-я
радиус –
вектором
т.А.
Траект-я движ-я будет опр-ся ф-ей
(t).
Для того, чтобы установить связь между
этими двумя способами описания, введем
три единичных вектора, орты
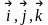 ,
направленных вдоль осей X,
Y,
Z,
соответственно. Тогда, как видно из
рисунка,
,
направленных вдоль осей X,
Y,
Z,
соответственно. Тогда, как видно из
рисунка,
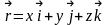 ,
,
а модуль радиус–вектора равен
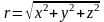 .
.
3) Естественный способ:
При естественном способе описания движения материальной точки, необходимо знать траекторию движения материальной точки. Тогда положение точки на траектории в разные моменты времени будет задаваться функцией пути от времени: s(t).
4.Перемещение. Скорость. Вычисление пройденного пути
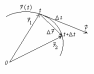
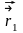 .
Рассмотрим достаточно близкий следующий
момент времени t
+ t.
.
Рассмотрим достаточно близкий следующий
момент времени t
+ t.
В
этот момент времени материальная точка
находится в точке 2,
и положение ее описывается радиус-вектором
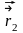 .
Тогда
.
Тогда
 , будет перемещение
материальной точки за время t,
а величина
, будет перемещение
материальной точки за время t,
а величина
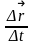 будет представлять среднюю скорость
точки на участке траектории 12.
Мгновенную скорость
будет представлять среднюю скорость
точки на участке траектории 12.
Мгновенную скорость
 определим как предел при t
0, т.е. как производную от радиус-вектора
.
определим как предел при t
0, т.е. как производную от радиус-вектора
.
 - скорость
при криволинейном движениии материальной
точки.Как
видно из рисунка скорость
направлена по касательной к траектории.
Далее при t0
rs,
и модуль скорости v
равен производной от пути по времени
- скорость
при криволинейном движениии материальной
точки.Как
видно из рисунка скорость
направлена по касательной к траектории.
Далее при t0
rs,
и модуль скорости v
равен производной от пути по времени
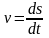 - модуль
вектора скорости.
- модуль
вектора скорости.
Как
всякий вектор, вектор скорости
можно выразить через его проекции на
оси координат:
 -
модуль вектора
скорости.
-
модуль вектора
скорости.
5.Ускорение. Нормальное и тангенциальное ускорение
В
механике вводится еще одна важная
характеристика движения – ускорение,
т.е. скорость изменения вектора скорости
во времени: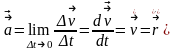 - ускорение
при криволинейном движении материальной
точки.
- ускорение
при криволинейном движении материальной
точки.
Учитывая
определение скорости
,
ускорение
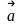 есть вторая производная от радиус-вектора
по времени t
(две точки означают вторую производную
по времени t).
Легко установить связь с координатным
представлением ускорения:
есть вторая производная от радиус-вектора
по времени t
(две точки означают вторую производную
по времени t).
Легко установить связь с координатным
представлением ускорения: -
модуль вектора
ускорения.
-
модуль вектора
ускорения.
Особенно удобен естественный способ представления ускорения.

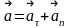
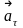 –
тангенциальное
ускор,
–
тангенциальное
ускор,
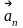 - нормальное ускорПриступим теперь к
опр-ю
и
.
Для этого нарисуем траекторию движения
(t)
и снова выберем два близких момента
времени t
и t
+ t.
- нормальное ускорПриступим теперь к
опр-ю
и
.
Для этого нарисуем траекторию движения
(t)
и снова выберем два близких момента
времени t
и t
+ t.
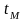 м. т.нахо-сь в точке 1
и скорость ее равнялась
м. т.нахо-сь в точке 1
и скорость ее равнялась
 ,
а в момент времени t
+ t
- в точке 2
и скорость ее равнялась
,
а в момент времени t
+ t
- в точке 2
и скорость ее равнялась
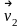 .
За время t
вектор скорости
изменился как по модулю, так и по
направлению. Для того, чтобы определить
.
За время t
вектор скорости
изменился как по модулю, так и по
направлению. Для того, чтобы определить
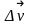 ,
перенесем вектор
в точку 1 и
представим
в виде суммы двух векторов
,
перенесем вектор
в точку 1 и
представим
в виде суммы двух векторов
 и
и
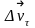 .
При этом модуль вектора
.
При этом модуль вектора

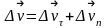 Согласно
опр-ю уск-я:
Согласно
опр-ю уск-я: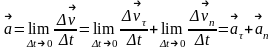 .
.
Как видно из построения,
 ,
и модуль вектора
равен производной от модуля вектора
скорости, т.е.
,
и модуль вектора
равен производной от модуля вектора
скорости, т.е.
 -
танг-е ускор
при крив-ом движении.
-
танг-е ускор
при крив-ом движении.
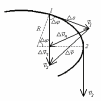
Для нахождения модуля вектора , сделаем дополнительные построения, а именно, в точках 1 и 2 проведем нормали к траектории и будем считать достаточно малый участок кривой 1–2 дугой окружности радиуса R . Тогда
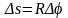 , откуда следует, что
, откуда следует, что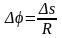 Зная
угол
, найдем модуль вектора
:
Зная
угол
, найдем модуль вектора
: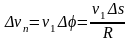 Возвращаясь
к определению
Возвращаясь
к определению
 ,
находим
,
находим -
нормальное
ускорение при криволинейном движении,гдеR-
радиус кривизны траектории.
-
нормальное
ускорение при криволинейном движении,гдеR-
радиус кривизны траектории.Рассмотрим два частных случая:
3Равномерное
движение материальной точки по окружности:
v
= const.
Тогда тангенциальное ускорение равно
нулю и полное ускорение равно нормальному,
т.е. центростремительному
ускорению: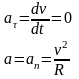 Прямолинейное
движение материальной точки:В
этом случае радиус кривизны траектории
равен бесконечности и нормальное
ускорение равно нулю. Полное ускорение
равно тангенциальному и направлено
вдоль направления движения: если а
0, по направлению движения, если а
0, против направления движения.
Прямолинейное
движение материальной точки:В
этом случае радиус кривизны траектории
равен бесконечности и нормальное
ускорение равно нулю. Полное ускорение
равно тангенциальному и направлено
вдоль направления движения: если а
0, по направлению движения, если а
0, против направления движения.

