
- •18) Условие жёсткой связи; неизменяемые мех-е сис-мы; Конфигурация мат-го тела; Теорема Грасгофа о проекциях скоростей.
- •19)Допустимые конфигурации мех. Сис-м;Коллинеарные точки неизменяемой мех. Сис-мы; Теорема о скоростях коллин. Точек.
- •20)Основное св-во допустимой конфигурации абсолютно тв. Тела; Задание конфигурации тв. Тела методом 3-х точек.
- •21)Связанная сис-ма отсчёта. Задание конфигурации атт методом связанных осей. Нахождение текущего положения телесной точки по её координатам в связанных осях.
- •22)Оператор ориентации абсолютно твёрдого тела. Ортогональность оператора ориентации. Основная формула геометрии движения.
- •23)Поступательное движение тв. Тела. Теорема о критерии поступательного движения. Траектории, скорости и ускорения телесных точек при поступательном движении.
- •24)Компоненты и матрица линейного оператора; формулы для компонент линейного оператора. Матрица направляющих косинусов тв. Тела.
- •25)Транспонирование линейных операторов. Св-ва матрицы направляющих косинусов.
- •1)Момент силы относительно точки
- •2)Вычисление проекции момента силы. Антисимметричные матрицы. Момент силы относительно оси
- •4)Аксиомы статики: общие аксиомы о силах. Следствие о переносе силы вдоль линии действия
- •10)Условия равновесия твёрдого тела при наличии трения(точечный и поверхностный контакт)
- •12) Способы задания движения точки
- •13) Скорость точки в в-ом и координатном способах задания движения
- •14)Скорость при естественном способе задания движения точки
- •17)Лемма об уравнениях сближения двух точек по экспоненте
- •3)Сис-мы сил и их эквивалентность. Главный вектор и главный момент сис-мы сил. Теорема об изм-ии гл. Момента при смене полюса.
- •5) Аксиомы статики: аксиома о связях. Реакции связей.
- •6) Теорема о приведении произвольной системы сил к двум силам.
- •7) Пара сил, её плечо и момент. Теорема о приведении произвольной сис-мы сил к силе и паре.
- •8) Теорема об условиях равновесия атт. Ур-я равновесия для пространственной сис-мы сил
- •9)Ур-е равновесия для плоской и сходящейся сис-мы сил, для сис-мы параллельных сил. Статистически определяемые задачи.
- •11)Законы трения скольжения(при покое). Закон Амантона-Кулона. Задача о трибометре.
2)Вычисление проекции момента силы. Антисимметричные матрицы. Момент силы относительно оси
 ,
где
,
где
 -компоненты
в-ра
-компоненты
в-ра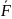 в осях Oxyz;
в осях Oxyz;
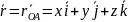 ,
где x,y,z-
координаты т.А в осях Oxyz
,
где x,y,z-
координаты т.А в осях Oxyz
Момент
силы
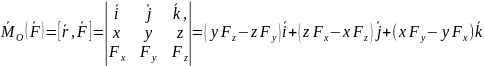
Компоненты
в-ра
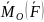 в
осях Oxyz
в
осях Oxyz
(*)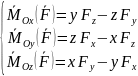
Введём
столбцы компонент в-ов

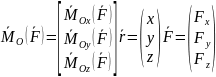 р-во
сводится к одному матричному р-ву
р-во
сводится к одному матричному р-ву
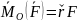 ,
если
,
если
 ,
матрица
,
матрица
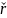 антисимметрична
антисимметрична
Последнюю
ф-лу (*) можно представить в виде (**) - Ф-ла Пуансо,
тк в неё не входит z,
след проэкция момента ситы на ось не
изменится, при сдвиге полюса вдоль этой
оси.
- Ф-ла Пуансо,
тк в неё не входит z,
след проэкция момента ситы на ось не
изменится, при сдвиге полюса вдоль этой
оси.
Момент
силы относительно оси-
скалярная величина = проекции на эту
ось момента силы относительно точки,
лежащей на данной оси. Можно вычислить
проэцируя р-ро на ось BZ
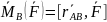 ,
вместо последней ф-лы(*)
,
вместо последней ф-лы(*)
4)Аксиомы статики: общие аксиомы о силах. Следствие о переносе силы вдоль линии действия
1)Аксиома параллелограмма сил
Состояние
тела не нарушится, если 2 силы, приложенные
в одной точке заменить их геометрической
суммой
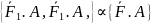 ,
где
,
где
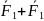 =
=
2)Аксиома о нуль системе
Состояние нуль системе не изменится, если к действующей на него системе сил добавить(отбросить) нуль систему
Тело на движение которого не наложено никаких наперед заданных ограничений называется свободным.
3)
Свободное АТТ под действием двух сил
находится в равновесии тогда и только
тогда, когда эти силы: Равны по модулю,
противоположны по направлению, лежат
на одной прямой ( )
–элементарная нуль система
)
–элементарная нуль система
Следствие(о переносе силы вдоль линии действия)
Силу приложенную к АТТ можно переносить вдоль линии действия в любую точкуне меняя состояния тела
Док-во
Пусть
к телу приложена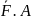 ,
а B
лежит на её линии действия. Приложим к
телу также
,
а B
лежит на её линии действия. Приложим к
телу также
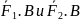 :
:
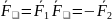 ,
,
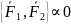 по
аксиоме 3;
по
аксиоме 3;
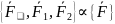 по акс2
по акс2
Итак
{
}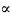
 },
те
},
те

Вывод: Силу приложенную к АТТ, можно рассматривать как скользящий вектор. 2и 3 аксиомы применимы только к АТТ.
4)Аксиома о действии и противодействии:
Если
на тело 1 с силой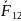 воздействует тело 2, то на тело 2 со
стороны тела 1 действует сила
воздействует тело 2, то на тело 2 со
стороны тела 1 действует сила
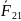 ,
причём эти силы: Равны по модулю,
противоположны по направлению, лежат
на одной прямой.
,
причём эти силы: Равны по модулю,
противоположны по направлению, лежат
на одной прямой.
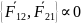 тк
они приложены к разным телам
тк
они приложены к разным телам
10)Условия равновесия твёрдого тела при наличии трения(точечный и поверхностный контакт)
Возможные перемещения при наличии трения те же что и при его отсутствии
Если
трение имеется, то при отбрасывании
данной связи её действие заменяется
силой
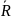 .K
и парой сил с моментом
.K
и парой сил с моментом
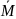 .
Проекция реакции R
на внешнюю нормаль неотрицательна,
трение препятствует движению не не
запрещает его. Разложив всё на касательную
и нормальную составляющие получим:
N-нормальная
составляющая реакции, Fтр-
трение скольжения(препятствует
скольжению), Mкач-
момент тр. качения, Mверч-
момент тр. Верч(препятствует вращению
вокруг внешней нормали)
.
Проекция реакции R
на внешнюю нормаль неотрицательна,
трение препятствует движению не не
запрещает его. Разложив всё на касательную
и нормальную составляющие получим:
N-нормальная
составляющая реакции, Fтр-
трение скольжения(препятствует
скольжению), Mкач-
момент тр. качения, Mверч-
момент тр. Верч(препятствует вращению
вокруг внешней нормали)
Условие
равновесия
 +
=0,
+
=0,
 +
+ =0,
где
и
главный вектор и главный момент активной
силы. Разложив их получим
=
=0,
где
и
главный вектор и главный момент активной
силы. Разложив их получим
=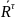 +
+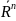 ,
,
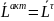 +
+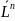 Вывод: при равновесии в примере 1 имеем
(*)
тр=-
,
Вывод: при равновесии в примере 1 имеем
(*)
тр=-
,
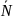 =-
,
Mкач=-
=-
,
Mкач=- ,
Mверч=-
.
Условие (*) необходимое но не достаточное.
Для равновесия необходимо (**) |
тр|<=
Fтрмах,|
кач
|<= Mкачмах,
|
верч
|<= Mверчмах
,
Mверч=-
.
Условие (*) необходимое но не достаточное.
Для равновесия необходимо (**) |
тр|<=
Fтрмах,|
кач
|<= Mкачмах,
|
верч
|<= Mверчмах
Сухое - тр в отсутствии смазки
Вязкое - тр при наличии смазки
