Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель

Дифференциальное уравнение вида

называется дифференциальным уравнением в полных диффернциалах, если его левая часть является полным дифференциалом некоторой гладкой функции   , т.е. если  ,   . Необходимое и достаточное условие для существования такой функции имеет вид:

Чтобы решить дифференциальное уравнение в полных дифференциалах необходимо найти функцию   . Тогда общее решение дифференциального уравнения можно записать в виде   для произвольной постоянной   .

Интегрирующим множителем для дифференциального уравнения

называется такая функция   , после умножения на которую дифференциальное уравнение превращается в уравнение в полных дифференциалах. Если функции   и  в уравнении имеют непрерывные частные производные и не обращаются в ноль одновременно, то интегрирующий множитель существует. Однако, общего метода для его отыскания не существует.

Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

   Рассмотрим уравнение вида

F ( x , y , y ' ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него  y ' ,  то можно получить , вообще говоря , несколько уравнений

Геометрически это означает ,  что в каждой точке   задаётся несколько направлений поля (см.рис.2).

Рис. 2

   Следовательно через любую точку  M ( x , y )  может проходить несколько интегральных кривых     . Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку  M₀ ( x₀ , y₀)  , надо помимо значений  ( x₀ , y₀ )    дополнительно задать в этой точке направление поля    y ' ( x₀) = y '_{0   .}

  

 21.Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами 

Линейным дифференциальным уравнением n -го порядка называется уравнение вида  y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),  где y = y(x) — неизвестная функция,  a1(x), a2(x), ..., an-1(x), an(x),  f(x) — известные функции, которые будем полагать непрерывными на промежутке (a, b).

Выражение в левой части уравнения называется линейным дифференциальным оператором n -го порядка:  L(y) = y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y .  Уравнения  y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = 0 и  y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),  f(x) № 0,  называются соответственно однородным и неоднородным линейным дифференциальным уравнением n -го порядка.

     Характеристическое уравнение 

 - корни характеристического уравнения.

     Общее решение 

     1. Все корни характеристического уравнения различные, тогда

     Если среди корней есть пары комплексно-сопряженных корней, например  , решение можно записать в виде

     2. Среди корней характеристического уравнения есть кратные, например,   имеет кратность k (остальные - простые), тогда

     Если среди корней есть пары сопряженных корней кратности k, например  , решение можно записать в виде

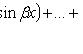
     Линейное неоднородное уравнение с постоянными коэффициентами 

     Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решения   неоднородного уравнения.

ФСР – все частные линейно независимые решения.

Критерий фундаментальности:

Чтобы n решений { y₁,y₂,…,y_n} ЛОДУ n-го порядка были линейнонезависимы, не и достаточно, чтобы определитель был отличен от 0 на (a;b).

Теорема об общем решение ЛОДУ:

Если функция { y₁,y₂,…,y_n} образует ФСР ЛОДУ n-го порядка, то его общее решение

y_oo=С_1у1(х)+С_2у2(х)+...+С_nуn(х)

22. Уравнением Эйлера называется однородное дифференциальное уравнение вида

xⁿy⁽ⁿ⁾ + a_n-1x^n-1y^{(n - 1)} + ... + a₁xy' + a₀y = 0.

Коэффициенты a_n-1, ... , a₁, a₀ — постоянные десйствительные числа.

Если функция y(x) — решение уравнения Эйлера, то функция Cy(x) тоже является решением уравнения.

Уравнение Эйлера заменой x = e^t сводится к однородному линейному уравнению с постоянными коэффициентами.

Выполним замену x = e^t, перейдём к новой переменной t = ln x :

Здесь α_ij — коэффициенты, которые легко вычисляются при последовательном дифференцировании.

После подстановки в уравнение имеем:

Решим это однородное линейное уравнение с постоянными коэффициентами — его общее решение g = g(t,C₁, C₂, ... ,C_n). Вернувшись к переменной x, получим общее решение уравнения Эйлера: y(x,C₁, C₂, ... ,C_n) = g(lnx,C₁, C₂, ... ,C_n).

23.

Теорема 5.1 (структура общего решения ЛНДУ). Общим решением у уравнения (5.1) является сумма его произвольного частного решения у* и общего решения   соответствующего однородного уравнения (5.2), т. е.

Убедимся, что функция (5.3) - решение уравнения (5.1). Так как у* есть решение уравнения (5.1), а - решение уравнения (5.2), то

В таком случае имеем:

Это означает, что функция является решением уравнения (5.1).

Покажем теперь, что функция

является общим решением уравнения (5.1). Для этого надо доказать, что из решения (5.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

Продифференцировав функцию (5.4) и подставив начальные условия (5.5) в функцию (5.4) и ее производную, получим систему уравнений:

где у_о=у(х_о), у'₀=y'(x₀), с неизвестными c₁ и с₂. Определителем этой системы является определитель Вронского W(x₀) для функции y₁(x) и у₂(х) в точке х=х_о. Функции y₁(x) и у₂(х) линейно независимы (образуют фундаментальную систему решений), т. е. Следовательно, система имеет единственное решение: c₁=с⁰₁ и с₂=с⁰₂.

Решение является частным решением уравнения (5.1), удовлетворяющим заданным начальным условиям (5.5). Теорема доказана.