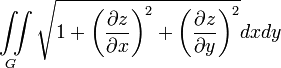- •2. . Он называется сходящимся, если существует конечный предел частичного интервала . В противном случае он расходящийся.
- •14.Достаточные условия экстремума функции многих переменных с использованием второго дифференциала и критерия Сильвестра.
- •15. Определение двойного интеграла
- •1.2. Основные свойства двойного интеграла
- •1.4. Геометрическая трактовка двойного интеграла
- •20. Интегрируемые типы уравнений первого порядка
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения первого порядка
- •Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель
- •Дифференциальные уравнения первого порядка, не разрешённые относительно производной .
- •24 Метод вариации произвольных постоянных
- •Остаточные признаки сходимости знакоположительного ряда.
- •Сходящиеся, абсолютно сходящиеся и условно сходящиеся комплексные ряды
- •Функции комплексной переменной как суммы абсолютно сходящихся степенных рядов. Формула Эйлера
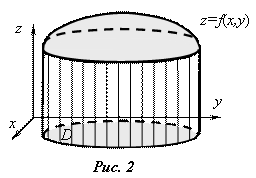
1.4. Геометрическая трактовка двойного интеграла
Цилиндроид,
или цилиндрическое
тело — это
пространственное тело, ограниченное
снизу областью D |
|
Двойной интеграл от функции f(x,y) по области D равен объему цилиндроида
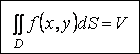
Для пояснения этого утверждения в определении двойного интеграла (2) проводим следующие геометрические истолкования: f(Pi)∙DSi = DVi — это объем элементарного цилиндра с основанием DSi и высотой f(Pi);
z = f(x,y),
проецируемой на область D,
так как при
Рис. 23.3
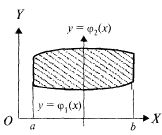
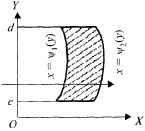
Рис. 23.4 Граница
области D, правильной в направлении
оси OY (рис. 23.3), может быть задана
уравнениями
причем
сначала вычисляется внутренний
интеграл в котором х считается постоянной. Выражение справа в (23.5) называется повторным, или двукратным интегралом. 17. Если полярную и декартову прямоугольную системы совместить так, чтобы начала их координат совпадали, а полярная ось совпадала с положительным направлением оси абсцисс прямоугольной системы, то независимо от расположения точки B на плоскости получим формулы перехода от полярных координат r, a к декартовым x, y: x = r cos a; y = r sin a (1) и от декартовых к полярным:
Например, уравнение r = c, где c = const, в полярных координатах определяет окружность с центром в полюсе и радиусом c. Используя формулы перехода (1), получаем уравнения координат точек кривой окружности: x = c cos a y = c sin a, которые называются параметрическими |
18)
Приложения двойных интегралов
Наименование величины |
Общее выражение |
Прямоугольные координаты |
Полярные координаты |
Площадь плоской фигуры |
|
|
|
Масса тонкой плоской пластинки плотностью |
|
|
|
Площадь
куска поверхности |
|
|
|
Объем цилиндрического тела, стоящего
на плоскости |
|
|
|
19)
формулировка:
Пусть
дана непрерывная
функция на отрезке ![]() Пусть
также
Пусть
также ![]() и
без ограничения общности предположим,
что
и
без ограничения общности предположим,
что ![]() Тогда
для любого
Тогда
для любого ![]() существует
существует ![]() такое,
что
такое,
что ![]() .
.
Задача
Коши –
это задача нахождения частного решения
дифференциального уравнения,
удовлетворяющего заданным начальным
условиям ![]() ,
где
,
где ![]() -
числа.
-
числа.
Если ![]() ,
то уравнение
,
то уравнение ![]() называют линейным
однородным дифференциальным уравнением
(ЛОДУ), в противном случае –линейным
неоднородным дифференциальным уравнением
(ЛНДУ).
Когда
коэффициенты
называют линейным
однородным дифференциальным уравнением
(ЛОДУ), в противном случае –линейным
неоднородным дифференциальным уравнением
(ЛНДУ).
Когда
коэффициенты ![]() являются
постоянными функциями (то есть, некоторыми
числами), то соответствующие дифференциальные
уравнения называют ЛОДУ
с постоянными коэффициентами (если
)
или ЛНДУ
с постоянными коэффициентами (при
ненулевой f(x)).
Характеристическое
уравнение линейного
однородного дифференциального
уравнения n-ой степени
с постоянными коэффициентами – это
уравнение n-ой степени
вида
являются
постоянными функциями (то есть, некоторыми
числами), то соответствующие дифференциальные
уравнения называют ЛОДУ
с постоянными коэффициентами (если
)
или ЛНДУ
с постоянными коэффициентами (при
ненулевой f(x)).
Характеристическое
уравнение линейного
однородного дифференциального
уравнения n-ой степени
с постоянными коэффициентами – это
уравнение n-ой степени
вида ![]() .
.