8.Задачи, приводящие к понятию опред интеграла(площадь криволинейной трапеции, длина дуги кривой, пример из экономики)

Площадь прямолинейной трапеции

Пусть на отрезке [a;b] задана непрерывная ф-ция y=f(x)

Рассм фигуру огранич кривой y=f(x), прямыми х=а и х=b и снизу осью Ох, прямой у=0. Поставим задачу опред площади это трапеции АВва, для этого разобьём отрезок [a;b] на n частей точками: ;проведём прямые и получ n прямых трапеций. Выберем на каждом из отрезков [ ],k=1,n произвольную точку и рассм знач ф-ции в этих точках. Каждую криволин трапецию заменим прмоугольником с высотой F от

Это равенство будет тем точнее,чем меньше длина прямоугольника:

H=max );1≤k≤n

S=

Число S наз опред интегралом от ф-ции f(x) по отрезку [a;b] и обознач:

S=

Длина дуги кривой. Пусть ф-ция y=f(x) непрерывна на отрезке[a;b]. найдём длину дуги ab.

Для этого разобьём ab точками , где совпадёт с точкой a. Соединим 2 соседние точки хордами . Получим ломаную из n звеньев вписанную в кривую АВ. Пусть -длина ломаной;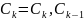

Если через L обозначим длину кривой, то L )

Если через W обозначим max из длин 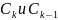;W=max ;1≤k≤n, то пользуясь формулой расстояния между двумя точками сначала можно найти длину каждого из отрезков:

K=1,n; ;

L=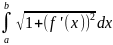

Пример из экономики.

Известно, что производит труда в теч раб дня меняется. Предположим, что известна непрерывная ф-ция f(x), кот характер изменением производит труда от времени. Опред объём продукции произведённой рабочим за промежуток времени от до . Искомый объём можно рассматр как сумму объёма продукции произведённой за бесконечно малые отрезки времени. Рассм разбиение отрезка [ , ] на части:

=

W=max( );1≤k≤n; тогда:

V

V

Признак сравнения :если на пром [a; непрерывные ф-ции f(x) и g(x) удовлет условию 0≤f(x)≤g(x), то из сходимости интегралов →сходимость интеграла ; а из расходимости интеграла расходимость интеграла

Несобвс. интегралы от неогранич ф-ций

Пусть нарушено пункт 2;предположим,что ф-ция f(x) интегр-ма на люб отрезке [a;c) [a;b), т.е. сущ

; если сущ , то его назыв несобств интегралом 2 рода или несобств интегралом от неогранич ф-ции.

Если предел сущ и конечен,то

Наз сходящимся;в противном случае расходяшимся.

Если ф-ция f(x) определена на пром (a;b] и неограничена в окресности точки х=а,то полагают,что

Если ф-ция f(x) определена на интерв (a;b) и неограничена при х=а, х=b, то

+

Если ф-ция f(x) явл неогранич во внутрен точке х=с отрезка [a;b], то несобств интеграл 2 рода опред формулой:

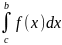= + (5)

В формуле (5) интеграл будет сходящимся, если оба несобств интеграла стоящих справа будут сходящимися.

Признак сходимости несобств интегралов 2 рода:

Пусть на пром [a;b)ф-ции f(x) и g(x) непрерывны при х=b и удовлет условию 0≤ f(x)≤ g(x), тогда из сходимости интеграла →сходимость ; а из расходимости расх