1. Определение ф-ии нескольких переменных.

Пусть задано множ. D упорядоченных пар чисел (x;y)Є D сопоставляет одно число z Є R₁ называется функцией нескольких переменных, определённых на множестве D со знач. R₁ и записывается в виде z=f(x;y) или f : D→ R. При этом x и y наз. аргументами, а z — функцией.

Предел ф-ии.

A=lim f(x;y) или A= lim f(M)

x→x₀ M→M₀

y→y₀

Непрер. ф-ии.

Ф-я z=f(x;y)(или f(M)) наз. непрер. в т. M₀(x₀;y₀), если она: а) определена в этой т. и некот. её окрестности. б) имеет предел

lim f(M)

M→M₀

в)этот предел равен знач. ф-ии z в т. M₀

2. Частные произв. и диф. ф-ии 2-ух перем.

произв:

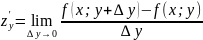
диф: dz=A∙Δx+B∙Δy

выражения A∙Δx+B∙Δy наз. частными диф.

3. Производн. сложных и неявно задан. ф-ий.

Если z=f(x;y)— диф-ма в т. M(x;y) Є D ф-я и x=x(t) b y=y(t)— диф-мые ф-ии независимой переменной t, то произв. сложной ф-ии z(t)=f(x(t);y(t)) вычисляются по формуле

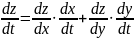
3. Понятие диф-сти ф-ии 2-ух переменных.

Пусть ф-я z=f(x;y) опред. в некот. окрестности т. M(x;y). Составим полное приращение ф-ии в т. M:

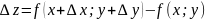
ф-я z=f(x;y) наз. диф-емой в т. M(x;y), если её полное приращение в этой т. можно представить в виде

3. Произв. по направлению.

Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

3. Поверхности уровня. Уравнение касательной плоскости к поверхности

Если равнодействующая сил, приложенных к материальной точке, имеет П. функцию V, то все пространство, в котором может находиться точка, можно представить себе заполненным системою бесконечного множества поверхностей, на каждой из которых V имеет одну и ту же величину. Такие поверхности называются поверхностями уровня;

уравнение касательной плоскости для неявно заданной ф-ции имеет вид:

уравнение касательной плоскости для явно заданной ф-ции имеет вид:

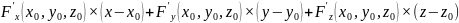
7. Касательная плоскость и нормаль к поверхности.

Пусть ф-я z=f(x;y) диф-ма в т. (x₀;y₀) некот. обл. D Є R². Рассечём пов. S, изображающую ф-ю z, плоскостями x=x₀ и y=y₀. Плоскость x=x₀ пересекает пов. S по некот. линии z₀(y), уравнение которой получается подстановкой в выражение исходной ф-ии z=f(x;y) вместо x числа x₀. Точка M₀(x₀;y₀;f(x₀;y₀)) принадлежит кривой z₀(y). В силу диф-сти функции z в т. M₀ ф-я z₀(y) также является диф-ой а т. y=y₀. Следовательно, в этой т. в плоскости x=x₀ к кривой z₀ может быть проведена касательная l_1­. Проводя анологич. рассуждения для сечения y=y₀ построим касательную l₂ к кривой z₀(x) в т. x=x₀. Прямые l₁ и l₂ определяют плоскость α, которая наз. касательной плоскостью к пов. S в т. M₀.

Прямая, проходящая через т. M₀ и перпендикулярна касательной плоскости, построенной в этой т., наз. её нормалью.

7. Экстремумы ф-ций двух переменных

Пусть задана функция двух переменных z=z(x,y), (x,y) D. Точка M₀(x₀;y₀) - внутренняя точка области D.

Если в D присутствует такая окрестность UM₀ точки M₀, что для всех точек

то точка M₀ называется точкой локального максимума. А само значение z(M₀) - локальным максимумом.

А если же для всех точек

то точка M₀ называется точкой локального минимума функции z(x,y). А само значение z(M₀) - локальным минимумом.

Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y).