1.Первообразная,примеры первообразных.

Ф-ция F(х) наз. Первообразной для ф-ции f(х) на промежутке (a;b), если для люб х из промежутков (a;b) ф-ция F(x) дифференцируема и выполняется равенство: F’(х)=f(x)

Заметим, что задача от искания по ф-ции f(x) её первообразной F(х) неоднозначна, а именно, если F(x) первообразная для ф-ции f(x), то и F(x)+C также явл первообразной для ф-ции f(x), т.к. если:

(F(x)+C)’=F’(x)

Пример:F(x)=ln(x);F(x)-?;f(x)=1/x

2.Определение неопределённого интеграла. Примеры.

Совокупность всех первообразных ф-ций для ф-ции f(x) на проме (a;b) наз неопред интегралом от ф-ции f(x)на этом промежутке и обозн: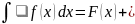 C

Операция нахождения первообразной по её производной или неопред интеграла по заданной подыинтегр ф-цией наз интегрированием этой ф-ции. Для проверки правильности интегр-я, нужно продиффер-ть результат и получитт подынтегр ф-цию. Пример:

Проверка( )’=2x

5.Основные методы интегрирования(подведение функции под знак дифференциала, метод подстановки, интегрирование по частям).

Если числитель подынтегральной ф-ции равен производной знаменателя, то интеграл равен логарифму от знаменателя:

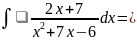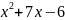ln( )+C

Метод подстановки: явл одним из эффективных способов сведения интеграла к табличному .Он основан на след теореме:

Пусть ф-ция x=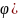 ) определена и дифференцируема на некот промежутке Т, а Х множество значений этой ф-ции на кот определена ф-ция f(x), тогда если ф-ция f(x) имеет первообразную на множестве Х, то на множестве Т справедлива формула:

Формула замены переменной в неопред интеграле.

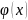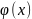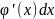Если подынтегральная ф-ция явл произвед 2х множителей, 1 из кот зависит от некот ф-ции ,а др явл производной , то целесообразно сделать замену перем-ой по формуле =u, тогда дифференциал от d( )=du→ =du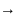

=

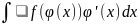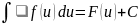
Такого рода преобразования наз подведение множителя под знак дифференциала.

Правильные рац дроби вида:

1.A/x-a

2.A/

3.Mx+N/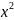 +px+q, где Д<0

4.Mx+N/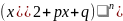

Интегрир-е дробей 1 и 2 типов производится с помощью формул 5 и 4 таблицы неопред интегралов. Для нахождения интеграла дроби 3 типа в случае М≠0 нужно в числителе выделить производную знаменателя и разложить полученный интеграл на сумму интегралов, тогда первый из них находится подстановкой +px+q=u, а второй сводится к табличному путём выделения в знаменателе полного квадрата. В случае М=0 интеграл берётся путём выделения в знаменателе полного квадрата

Схема интегр-я рац дробей:

1.если дробь P(x)/Q(x) неправильная, то выделяют целую часть, т.е. представляют эту дробь в виде суммы многочлена и правильной рац дроби.

2.раскладывают знаменатель Q(x) на лин и квадратные множители, причём квадратич множители не должны иметь действит корней. Если есть совпадающие множители их группируют.

3.записывают разложение правильной рац дроби на сумму простейших дробей с неопред коэфф. Находят неизвестные коэфф либо способом сравнения коф,либо способом частных значений, либо комбинацией этих 2х способов.

4.представляют интеграл от данной рац дроби в виде суммы интегралов от целой части и от простейших рац дробей и находят эти интегралы.