
- •1. Определение первообразной и её свойства
- •2. Неопределённый интеграл,таблица основных интегралов
- •3. Инвариантность формул интегрирования
- •4.Непосредственное интегрирование
- •5,Интегрирование методом замены переменной(метод подстановки)
- •6. Метод интегрирования по частям
- •7.Примеры интегрирования рациональных функций
- •8 .Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •9.Разложение рациональных функций в сумму простейших дробей
- •10.Интегрирование иррациональных функций
- •14. Определенный интеграл
- •15.Методы вычисления определенного интеграла
- •17. Формула Ньютона Лейбница
- •20. Дифференциальные уравнения первого порядка
- •21. Задача Коши.
- •22.Теорема существования и единственности решения задачи Коши.
- •23. Уравнения с разделяющимися переменными
- •Уравнения вида
- •24. Ду с однородными функциями
- •25.Линейные дифференциальные уравнения первого порядка
- •Преобразованное уравнение является линейным относительно и . Решив его, найдем общий интеграл уравнения Далее, подставив , получим общее решение уравнения Бернулли
- •27.Уравнение в полных дифференциалах
- •Уравнение может быть записано в виде
- •28.Ду высших порядков…..
- •31.Свойства решений лоду
- •32. Определитель Вронского
- •33. Структура общего решения лоду
- •36. Метод вариации произвольных постоянных
- •38.Лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
- •Вычисление длины дуги плоской кривой
5,Интегрирование методом замены переменной(метод подстановки)
Пусть
 имеет первообразную, а
имеет первообразную, а
 непрерывна и дифференцируема, тогда
непрерывна и дифференцируема, тогда
 .
(4)
.
(4)
Пример. Найти
 .
.
Чтобы
избавиться от корня, полагаем
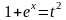 ,
отсюда
,
отсюда
 .
Найдем
.
Найдем
 .
Для этого продифференцируем равенство
.
Для этого продифференцируем равенство
 ,
получим
,
получим
 ;
тогда
;
тогда
 .
Подставим
.
Подставим
 в подынтегральное выражение; получим
интеграл вида:
в подынтегральное выражение; получим
интеграл вида:
 .
.
Итак,


6. Метод интегрирования по частям
Пусть
 и
и
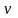 - непрерывно дифференцируемые функции
от
- непрерывно дифференцируемые функции
от
 .
На основании формулы дифференциала
произведения имеем
.
На основании формулы дифференциала
произведения имеем
 .
.
Интегрируя,
получим
 или
или
 .
(5)
.
(5)
Полученная формула
интегрирования по частям позволяет
сводить интеграл
 к более простому
к более простому
 .
.
Иногда формула интегрирования по частям применяется несколько раз.
Рекомендации по применению формулы интегрирования по частям приведены в таблице:
|
Вид подынтегральной функции |
Рекомендации |
Ожидаемое упрощение подынтегрального выражения |
|
|
Произведение многочлена
|
|
Под интегралом степень многочлена уменьшится на единицу |
|
|
Произведение многочлена на логарифмическую или обратную тригонометрическую функцию |
|
Под интегралом вместо трансцендентной функции появится алгебраическая функция |
7.Примеры интегрирования рациональных функций
Пример  =
= ;
;
 − это неправильная рациональная дробь.
Сначала выделим целую часть дроби,
разделив числитель на знаменатель.
− это неправильная рациональная дробь.
Сначала выделим целую часть дроби,
разделив числитель на знаменатель.
-


-
2
Тогда
 ,
где
,
где
 - целая часть дроби,
- целая часть дроби,
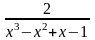 - правильная рациональная дробь,
знаменатель которой разлагается на
множители:
- правильная рациональная дробь,
знаменатель которой разлагается на
множители:
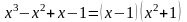 .
.
Корни знаменателя:
 ,
а
,
а
 не имеет действительных корней.
не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
 .
.
Приводя полученные дроби к общему знаменателю, получим тождество:
 .Приравнивая
числители обеих дробей, получим уравнение:
2=
.Приравнивая
числители обеих дробей, получим уравнение:
2= .
.
Пусть
,
тогда 2=2
 .
Коэффициенты
.
Коэффициенты
 найдем из системы:
найдем из системы:
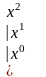
 Откуда
Откуда
 .
.
Тогда
= =
=
 =
=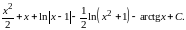
8 .Интегрирование рациональных дробей
Рациональной
дробью называется дробь вида
 ,
где
,
где
 и
и
 – многочлены степени
– многочлены степени
 и
и
 соответственно.
Рациональная дробь называется правильной,
если степень числителя меньше степени
знаменателя (
<
),
в противном случае дробь называется
неправильной.
соответственно.
Рациональная дробь называется правильной,
если степень числителя меньше степени
знаменателя (
<
),
в противном случае дробь называется
неправильной.
Пример

 ,
здесь
,
здесь

Алгоритм интегрирования рациональной дроби
Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
 ,
где
,
где
 многочлен,
а
многочлен,
а
 правильная
рациональная дробь.
правильная
рациональная дробь.
Знаменатель разложим на простейшие сомножители:
 ,
где многочлены
,
где многочлены
 не имеют действительных корней.
не имеют действительных корней.
Представим дробь в виде суммы простейших дробей с неопределенными коэффициентами , которые надо найти.
Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях .
Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
Подставим найденные коэффициенты
 в разложение дроби.
в разложение дроби.Проинтегрируем простейшие дроби.

 на показательную или тригонометрическую
функцию
на показательную или тригонометрическую
функцию






