1.

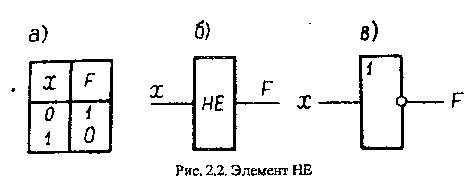
(х = 0, F = 1) и наоборот, нулевой сигнал на выходе появляется при единич­ном сигнале на входе (х = 1, F = 0). Элемент НЕ реализует функцию отрицания.

Функция логического умножения (конъюнкция)

Логическое умножение — это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единич­ным значениях всех переменных. Эта функция называется также конъюн­кцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты запи­си конъюнкции:

Конъюнкция характеризуется таблицей истинности, представленной на рис. 2.3 а. Из рассмотрения таблицы следует, что эта функция принимает еди­ничное значение на наборе 3. Логическое умножение описывает работу элемен­та И (рис. 2.3 б). Единичный сигнал появляется на выходе этого элемента только

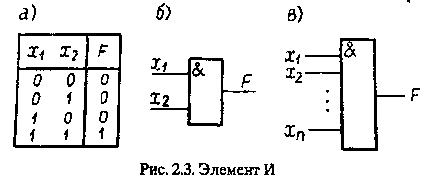
при наличии единичного сигнала и на входе 1, и на входе 2. Элемент И реализует функцию логического умножения. В общем случае элемент И может иметь п входов (рис. 2.3 в). При этом он реализует конъюнкцию от ппеременных т.е.:

2.

Отрицание от логического умножения (отрицание от конъюнкции)

Отрицание от логического умножения или отрицание от конъюнкции— логическая функция по крайней мере от двух переменных, которая это принимает нулевое значение при единичных значениях всех переменных. Эта функция называется также функцией Шеффера. Таблица истинности элементарной функции отрицания от конъюнкции представлена на рис. 2.4 а. функция принимает единичные значения на наборах 0,1,2 и нулевое значе­ние — только на наборе 3, т.е. тогда, когда обе переменные равны единице. Запись функции:

функция отрицания от конъюнкции описывает работу элемента И-НЕ, (рис. 2.4 б.). Нулевой сигнал на выходе этого элемента появляется только при наличии единичного сигнала и на входе 1 и на входе 2.

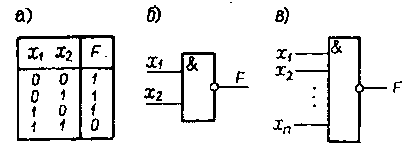
Рис. 2.4. Элемент И-НЕ

В общем случае элемент И-НЕ может иметь п входов (рис. 2.4 в). При этом он реализует функцию Шеффера от п переменных, т.е.:

Функция логического сложения (дизъюнкция)

Логическое сложение—это логическая функция по крайней мере от двух переменных, которая принимает нулевое значение при нулевых значениях всех переменных. Эта функция называется также дизъюнкцией.

Таблица истинности элементарной дизъюнкции представлена на рис. 2.5 а. Элементарная дизъюнкция принимает единичное значение на наборах 1> 2,3 и нулевое значение — только на наборе 0. Функция записывается в одном из двух видов:

Знак «плюс» не является алгебраическим, т.к. при дизъюнкция

т.е. она не может быть равной 2.

Дизъюнкция описывает функционирование элемента ИЛИ (рис. 25 а). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или или на двух входах есть единичные сигналы. И только в том случае,

3.

когда на оба входа поступают нулевые сигналы, на выходе элементов появ­ляется нулевой сигнал. Функционирование элемента ИЛИ полностью соот­ветствует таблице истинности для дизъюнкции.

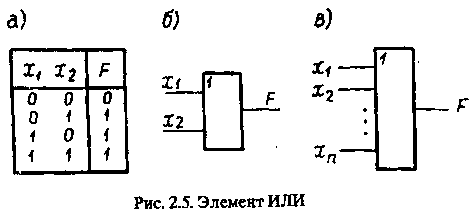
В общем случае элемент ИЛИ может иметь п входов (рис. 2.5 в). При этом он реализует дизъюнкцию от п переменных, т.е.: