48. Концентрации напряжений. Коэффициент концентрации.
В
близи
различного рода отверстий, надрезов,
выточек и, вообще,(мест резкого изменения
поперечных размеров распределение
напряжений становится существенно
неравномерным, и возникают зоны
повышенных напряжений. Например, при
одноосном равномерном растяжении
напряжениями σ тонкой пластинки шириной
Н с небольшим (d<Н/5) круглым отверстием
распределение напряжений по поперечному
сечению, проходящему через центр
отверстия, оказывается существенно
неравномерным с пиками напряжений в
точках А и В контура отверстия (4.21).
Точное решение показывает, что нормальные
напряжения в радиальных сечениях на
контуре отверстия изменяются по закону
σθ=σ(1-2cos2θ) и в точках А и В при θ=π/2
достигают величины σmax=3σ, а при θ=0, т.
е. в сечении, параллельном линии действия
нагрузки, действуют сжимающие напряжения
σθ=σ, равные по величине приложенным к
пластинке напряжениям.
Концентрация напряжений в пластине с отверстием
Неравномерность распределения напряжений по поперечному сечению имеет место и при центральном растяжении ступенчатого бруса , причем максимальные напряжения быстро увеличиваются по мере уменьшения радиуса закругления переходной части (галтели). Большие местные напряжения возникают также в зоне контакта деталей (контактные напряжения).
Явление
возникновения значительных местных
напряжений называется концентрацией
напряжений, а причина, вызвавшая
концентрацию - концентратором напряжений.
Концентрация напряжений характеризуется
коэффициентом концентрации α. Величину
α также называют теоретическим
коэффициентом концентрации. Коэффициентом
концентрации α называется отношение
действительного напряжения σmax в
наиболеенапряженной точке к номинальному
напряжению σn в той же точке, т. е.
или
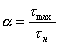
Номинальными называются напряжения, вычисленные по формулам сопротивления материалов, не учитывающим явление концентрации напряжений. В тех случаях, когда возникают трудности в вычислении номинальных напряжений в сечении с концентратором напряжений, за номинальные принимают напряжения в неослабленном сечении детали.
В
настоящее время методами теории
упругости и экспериментальными методами
(обычно путем испытания образцов из
оптически активного материала в
поляризованном свете) определены
величины коэффициентов концентрации
для многих практически важных случаев.
Расчетные формулы, таблицы и графики
для определения коэффициентов
концентрации приводятся в справочной
литературе.
На Рис представлен характер зависимости коэффициента концентрации от отношения радиуса галтели ρ к диаметру d в случае осевого растяжения ступенчатого бруса.