18.Принципы расчёта простейших статически неопределимых систем при растяжении-сжатии. Уравнение совместности деформаций.

Брусья и шарнирно-стержневые системы, в которых внутренние усилия от заданной нагрузки можно определить при помощи уравнений равновесия, называются статически определимыми. В отличие от них статически неопределимыми называются брусья и системы, внутренние усилия в которых нельзя определить при помощи одних лишь уравнений равновесия, называются статически определимыми. В отличие от них статически неопределимыми называются брусья и системы, внутренние усилия в которых нельзя определить при помощи лишь уравнений равновесия, поэтому при их расчёте необходимо составлять дополнительные уравнения(уравнения перемещений), учитывающие характер деформации системы. Число дополнительных уравнений, необходимых для расчёта системы, характеризует степень её статической определимости. Составляют дополнительные уравнения(уравнения перемещений), необходимые для решения задачи, они являются очень важными.

Порядок определения неизвестных усилий: 1) Определяем количество неизвестных усилий и составляем все возможные уравнения статики.2) стрим план деформации системы и находим уравнение совместимости деформаций 3) по закону гука выражаем деформации через усилия 4) решаем совместно уравнения статики и уравнения деформации.

Мысленно отбрасываем одну из заделок заменив её действие на стержень неизвестной реакцией, тем самым получим основную систему. Составляем уравнение совместимости деформаций, т.е. чтобы выполнить «граничное» условие ∆l=(N*l)/E*A

Иногда когда элементы конструкции лишины возможности свободно деформироваться, но t участков изменяется, о в конструкции возникают так называемые температурные усилия и соответствующие им температурные напряжения. ∆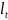 =α+∆t*l В теорию упругости входит еще одна группа уравнений – уравнения совместности деформаций. Если формулы Коши рассматривать как уравнения относительно трех неизвестных компонент перемещений u_x, u_y, u_z считая заданными шесть величин _ij, то для трех неизвестных получим шесть уравнений, то есть переопределенную систему. Эта система будет иметь решение только при выполнении дополнительных условий относительно _ij. Эти условия и есть уравнения совместности. Эти уравнения часто называют условиями сплошности, подразумевая при этом, что они обеспечивают сплошность тела после деформации. Это выражение образное, но неточное: эти условия обеспечивают существование непрерывного поля перемещений, если в качестве неизвестных принять компоненты деформаций (или напряжений). Невыполнение этих условий ведет не к нарушению сплошности, а к отсутствию решения задачи.

3.Основные гипотезы, допущения и принципы. 1.об однородности и изотропности мат. Матер предпол однор и изотр,т.е.в любом объеме и в любом напр св-ва матер счит один. Если св-ва неод, то мат счит анизотропным(древесина).2.гипотеза о «сплошности» мат. Предпол,что мат полностью заполняет весь объем тела без каких-либо пкстот. 3.о соверш упругости матер. Т.е.способн полн восстан первонач форму и размеры тела после после устран причин,вызвавш его деф.4.гипотеза о малости матер. Деф констр наст малы, что можно не учит их влияние на взаимн распол нагрузок.5.о линейной завис между деформ и напр.деф матер констр в к-й его т прямо пропорц напр в этой точке(закон Гука) он справедлив если знач напр не прев предел пропорц. 6.плоские сечения.попер сечения бруса,плоские до приложения нагр ,ост плоскими и при действ нагр.

24.Главные оси инерции. Главные моменты инерции. экстримальные(max,min)значения осевых моментов инерции сечения называются главными моментами инерции. Оси относительно к-х осевые моменты инерции имеют экстримальные знечения называются главными осями инерции.I_y1+I_z1=I_y+I_z из ф-лы следует, что если осевой момент инерции относительно некоторой оси является max, то осевой момент инерции относительно ей оси является min, так как  осевых моментов инерции относительно 2 взаимно осей не зависит от угла . Таким образом главные оси инерции взаимно. Относительно главных осей инерции центробежный момент инерции=0. Поэтому главными осями инерции можно называть оси, относит к-х центробежный момент инерции=0. tg2₀ =-2I_yz/(I_z-I_y) если 0, то оси откладываются против часовой стрелки, если 0, то по ходу часовой стрелки.

I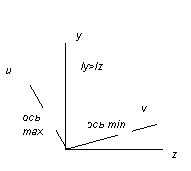 _max,min=

25. Вычисление моментов инерции сложных сечений. Способ вычисления моментов инерции сложных сечений основан на том, что любой интеграл можно рассматривать как  интегралов и, следовательно, момент инерции любого сечения вычислять как  моментов инерции отдельных его частей. Поэтому для вычисления моментов инерции сложное сечение разбивают на ряд простых частей с таким расчетом, чтобы их геометр хар-ки можно было вычислить по известным формулам или найти по табл. В ряде случаев при разбивке на простые фигуры для уменьшения их числа или упрощения формы сложное сечение целесообразно дополнять некоторыми площадками. после разбивки сложного сечения выбираем прямоугольную систему координат, относит к-й необходимо определить моменты инерции соответствующих частей.(координаты применяются ⃦ , чтобы путем переноса осей можно было подсчитать моменты инерции всех частей). Система координат для каждой простой фигуры применяется центральная, т.е. начало совпадает с центром тяжести. Далее вычисляются площади каждой простой фигуры, а также осевые и центробежные моменты инерции относительно осей координат. Полярный момент инерции вычисляют только для круглого сечения. Определяют момент инерции к-й простой фигуры относительно вспомагательных центральных осей. Определяют момент инерции всего сложного сечения относительгно этих осей.

34.Внешние силы вызывающие кручение рямого бруса. Кручением называется вид нагрузки при к-м в поперечном сечении бруса возникают только крутящие моменты. Такой вид нагрузки имеет место когда на брус действует пара сил лежащих в плоскости  к оси 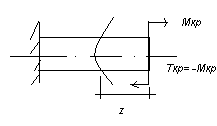бруса. Поперечное сечение бруса действ только момент к-й определяется методом сечения. Лев:Т+ по часов-й;Т- против часов-й ПРАВ:Т+ протии час-й;Т- по час-й.

в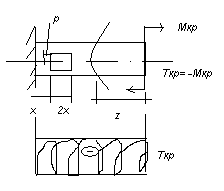 ыделим 2 поперечныхсечения и цилиндрическую поверхность радиусом  элемента бруса длинной dx. При расчете будут использовать следующие допуцения:1. Ось бруса при кручении остается прямой. 2. В пределах малых углов закручивания поперечные сечения до деф. плоские , остаются плоскими после деформации. 3. Деформ бруса при кручении заключается в повороте поперечного сечения относительно друг друга при сохранении между ними постоянных расстояний. Согласно данным гипотезам в поперечном сечении будет действовать только касательное напряжение.

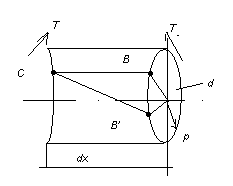под действием момента Т правое сечение элемента поварачивается относительно левого на угол d, при этом образующая СВ поворачивается на угол  и займет положение СВ’. дуга ВВ’ будет рассчитана по ф-ле. BB”=dx=d=d/dx , угол  хар-т изменение прямого угла и является углом сдвига. Величина d/dx-это угол закручивания приходящийся на единицу длины. = d/dx-относительный угол закручивания. =. Заменим угол  по закону Гука для сдвига=/G

=GG-модуль сдвига,const,Ю зависит от материала.

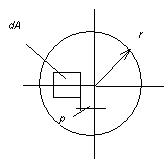 0;=0 r;_max. Для данного сечения можно предположить, что произведение G=const

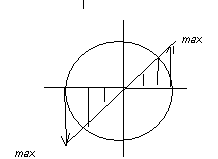эпюра  изменяется по линейному закону и имеет max значение на контуре. Выделим сечения элементарной площадки dA и определим значение крутящего момента. dT=dA подставив вместо -GT=_A²GdA=G_A²dA_A²dA =I_pT=I_pG

=T/I_pG где I_pG- жесткость конструкции при кручении. Если жесткость , то угол  и наоборот.

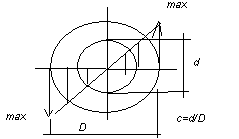основными характеристиками круглого и осевого сечения является полярный момент инерции и полярный момент сопротивления. Они необходимы при подборе размеров конструкции. КРУГ I_p=d⁴/32 W_p=d³/16 КОЛЬЦО I_p=d⁴/32 (1-c⁴) W_p=d³/16 (1-c⁴) также необходимо определить при расчете величину углового закручивания. Угол закручивания определяется по закону Гука. _i=T_il_i/GI_p (рад) =T_il_i/GI_p180/ (град).