
- •1. Задачи и методы термодинамики. Современное состояние и перспективы развития теплоэнергетики.
- •2.Термодинамическая система. Параметры состояния термодинамической системы. Уравнение состояния.
- •3. Термодинамический процесс. Равновесные, неравновесные, обратимые и необратимые процессы.
- •4. Первый закон термодинамики. Энтальпия.
- •6 . Цикл Карно. T-s - диаграмма. Изображение процессов в t-s- диаграмма.
- •7. Второй закон термодинамики. Изменение энтропии в термодинамических процессах. Статистическое толкование 2-ого закона термодинамики
- •8. Теплоемкость газов. Зависимость теплоемкости от температуры и процесса.
- •9. Политропный процесс. Обобщающее значение политропного процесса.
- •14. Паросиловые установки.
- •15.Элементарный и сложный теплообмен. Сложный теплообмен
- •16. Основной закон теплопроводности.
- •1.Геометрические; 2.Физические; 3.Граничные; 4. Начальные.
- •18. Стационарная теплопроводность через плоскую стенку
- •19. Стационарная теплопроводность через цилиндрическую стенку
- •20. Теплопередача через плоскую однослойную стенку.
- •22.Физическая сущность явления теплоотдачи.
- •23. . Основы теории подобия. (тп)
- •24) Теплоотдача при вынужденном течении по трубам и каналам.
- •29. Лучистый теплообмен между твердыми телами.
6 . Цикл Карно. T-s - диаграмма. Изображение процессов в t-s- диаграмма.
Рассмотрим цикл abfe на первом рисунке а, состоящий из двух изотерм ab и fe и двух произвольных равновесных процессов bf и еа, линии которых эквидистантны в T,s-диаграмме. Для равновесного нагрева рабочего тела по линии еа и охлаждения по линии bf нужно располагать бесконечно большим количеством источников теплоты, чтобы при каждой температуре в диапазоне Та—Т\ теплообмен между источником теплоты и рабочим телом протекал равновесно. Однако можно осуществить процесс так, чтобы теплота hq, выделяющаяся при охлаждении тела при температуре Т по линии bf, затрачивалась на нагрев тела при той же температуре по линии еа. Если линии еа и bf эквидистантны, то количества отданной при охлаждении (площадь М) и полученной при нагреве (площадь geah) теплоты одинаковы, т. е. теплота, выделенная при охлаждении по линии bf, полностью используется по линии еа. От горячего источника при температуре 7i по-прежнему подводится теплота, эквивалентная площади habk, к холодному источнику при температуре 7"? отводится теплота qz, соответствующая площади gefi.
Термический КПД данного цикла
![]()
Таким образом, равновесные циклы, подобные рассмотренному и осуществляемые также, как и цикл Карно, между двумя источниками теплоты имеют КПД, равные КПД цикла Карно. Они называются обобщенными циклами Карно.
Во всех других случаях любой цикл с верхней температурой Г, и нижней температурой Тг имеет термический КПД ниже, чем цикл Карно. На рис. 3.5, б изображен произвольный цикл efgk, осуществимый при наличии бесконечно большого количества источников теплоты. При одинаковых предельных температурах цикл Карно имеет более высокий термический КПД, чем любой другой цикл
7. Второй закон термодинамики. Изменение энтропии в термодинамических процессах. Статистическое толкование 2-ого закона термодинамики
А) Из первого закона термодинамики следует, что взаимное превращение тепловой и механической энергии в двигателе должно осуществляться в строго эквивалентных количествах. Двигатель, который позволял бы получать работу без энергетических затрат, называется вечным двигателем первого рода. Ясно, что такой двигатель невозможен, ибо он противоречит первому закону термодинамики. Поэтому первый закон можно сформулировать в виде следующего утверждения: вечный двигатель первого рода невозможен.
Несмотря на эквивалентность теплоты и работы, процессы их взаимного превращения неравнозначны. Опыт показывает, что механическая энергия может быть полностью превращена в теплоту, например, путем трения, однако теплоту полностью превратить в механическую энергию в периодически повторяющемся процессе нельзя. Многолетние попытки осуществить такой процесс не увенчались успехом. Это связано с существованием фундаментального закона природы, называемого вторым законом термодинамики.
Как показал опыт, все без исключения тепловые двигатели должны иметь горячий источник теплоты, рабочее тело, совершающее замкнутый процесс — цикл, и холодный источник теплоты.
Б
 )
Рассмотрим
принципиальные отличия неравновесных
процессов от равновесных на примере
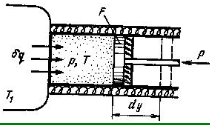
расширения газа в цилиндре под поршнем,
получающего теплоту δq
от
источника с температурой Т
и
совершающего работу против внешней
силы Р,
действующей
на поршень.
)
Рассмотрим
принципиальные отличия неравновесных
процессов от равновесных на примере
расширения газа в цилиндре под поршнем,
получающего теплоту δq
от
источника с температурой Т
и
совершающего работу против внешней
силы Р,
действующей
на поршень.
Расширение будет равновесным только в случае, если температура газа Т равна температуре источника (Т=Т1), внешняя сила Р равна давлению газа на поршень (P=pF) и при расширении газа нет ни внешнего, ни внутреннего трения. Работа расширения газа в этом случае равна δLрас = Pdy=pdv, а изменение энтропии рабочего тела в таком процессе ds=δq/T
Для изолированных систем, которые по определению не обмениваются теплотой с окружающей средой (δq=0), эти выражения приобретают вид δq >=0. Если в адиабатно-изолированной системе осуществляются равновесные процессы, то энтропия системы остается постоянной.
Самопроизвольные (а значит, и неравновесные) процессы в изолированной системе всегда приводят к увеличению энтропии. Это положение представляет собой наиболее общую формулировку второго начала термодинамики для неравновесных процессов, известную под названием принципа возрастания энтропии.
В) термодинамическая система представляет собой газ. Для определения ее состояния необходимо указать всего два макроскопических параметра, например давление и температуру. Но можно это состояние задать и по-другому, указав, например, положение и скорость каждой из частиц, входящей в систему. Таким образом, в первом случае мы задаем макро-состояние системы, во втором — ее микросостояние.
Очевидно, что одно и то же значение термодинамических параметров системы может получиться при различных положениях и скоростях ее частиц, следовательно, одному макро-состоянию системы отвечает ряд микросостояний. В статистической механике принято характеризовать каждое макро-состояние величиной Р — числом соответствующих микросостояний, реализующих данное макро-состояние. Величина Р называется термодинамической вероятностью данного макро-состояния.
Таким образом, энтропия изолированной системы в каком-либо состоянии пропорциональна натуральному логарифму вероятности данного состояния. Так как природа стремится от состояний менее вероятных к состояниям более вероятным, энтропия изолированной системы уменьшаться не может. Эти два утверждения являются, по сути дела, статистической и феноменологической формулировками второго начала термодинамики.
