
- •14. Разветвляющиеся программы.
- •14.1. Условный оператор if.
- •If Условие then Оператор1 else Оператор2;
- •If Условие then Оператор;
- •If Условие then if ПодУсловие then ... Else ...
- •14.2. Случайные величины.
- •14.3. Логические операции и выражения.
- •Логические операции и таблицы истинности
- •15. Циклические программы.
- •15.1. Оператор перехода Go To.
- •15.2. Операторы цикла Do.
- •1. Бесконечный цикл
- •2. Со счетчиком
- •3. C предусловием
- •15.3. Оператор цикла For.
- •16. Массивы данных.
- •16.1. Использование массивов при программировании.
- •16.2. Рекурсия.
- •16.3. Сортировка.
- •17. Элементы управления.
- •17.5. Списки (ListBox, ComboBox, CheckedListBox).
- •18. Объектное программирование.
- •18.1. Статические и динамические компоненты объектов.
- •18.2. Поля и свойства объектов.
- •18.3. Конструкторы.
- •Конструктор по умолчанию
- •Конструктор копирования
- •Конструктор преобразования
- •18.4. Наследование.
- •Простое наследование
- •Множественное наследование
- •18.5. Полиморфизм.
- •10. Организация поточных процессов.
- •10.1. Особенности поточной формы организации процессов.
- •10.2. Основные параметры поточных линий.
- •10.3. Виды поточных линий.
- •5. По характеру движения конвейера.
- •6. По уровню механизации процессов различают автоматические и полуавтоматические поточные линии.
- •7. По степени охвата производства.
- •9.1. Структура и длительность цикла процесса
- •9.5. Длительность производственного цикла сложного процесса
- •7. Основы организации процессов.
- •7.1. Принципы организации процессов.
- •7.2. Типы операционных систем.
14. Разветвляющиеся программы.
14.1. Условный оператор if.
Условный оператор IF служит для организации процесса вычислений (изменения последовательности выполнения операторов) в зависимости от какого-либо логического условия.
Синтаксис оператора IF:
If Условие then Оператор1 else Оператор2;
или
If Условие then Оператор;
Условие может быть представлено логической константой (FALSE – ложь, TRUE - истина), переменной логического типа (Boolean) или логическим выражением.
Если условие истинно, то выполняется оператор (простой или составной), следующий за словом THEN, в противном случае, когда условие ложно, будет выполняться оператор, следующий за словом ELSE. Альтернативная ветвь ELSE может отсутствовать, если в ней нет необходимости. В таком “усеченном” варианте, в случае, если условие оказывается ложным, ничего не происходит и выполняется оператор следующий за условным оператором IF.
Условные операторы могут быть вложенными друг в друга:
If Условие then if ПодУсловие then ... Else ...
ELSE ...;
Обратите внимание на отсутствие точки с запятой между ключевыми словами.
В условии оператора IF может стоять достаточно сложное логическое выражение.
14.2. Случайные величины.
Случайная величина - одно из основных понятий теории вероятностей. В самом общем смысле случайная величина - это некоторая переменная, принимающая, те пли иные значения с определенными вероятностями.
Случайная величина может быть:
дискретной (дискретно распределенной), когда она может принимать конечное или бесконечное счетное множество значений, элементы которого могут быть занумерованы и выписаны в последовательность x1, x2, ..., xn, ...;
непрерывной (непрерывно распределенной), когда она может принимать любые значения в одном или нескольких заданных интервалах или областях плоскости или пространства (существенным здесь является то обстоятельство, что эти значения образуют несчетное бесконечное множество, которое называют континуумом).
Зависимой и независимой.
14.3. Логические операции и выражения.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
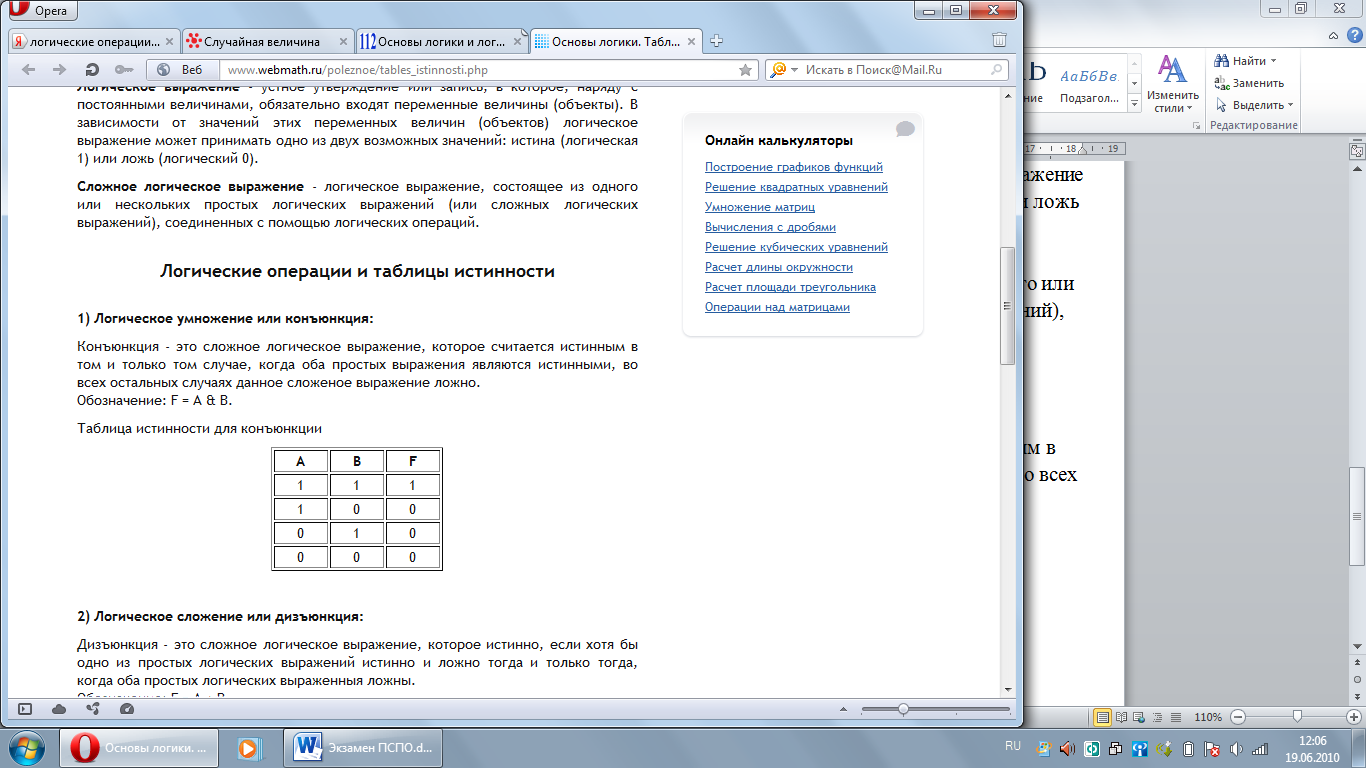
Таблица истинности для конъюнкции.
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
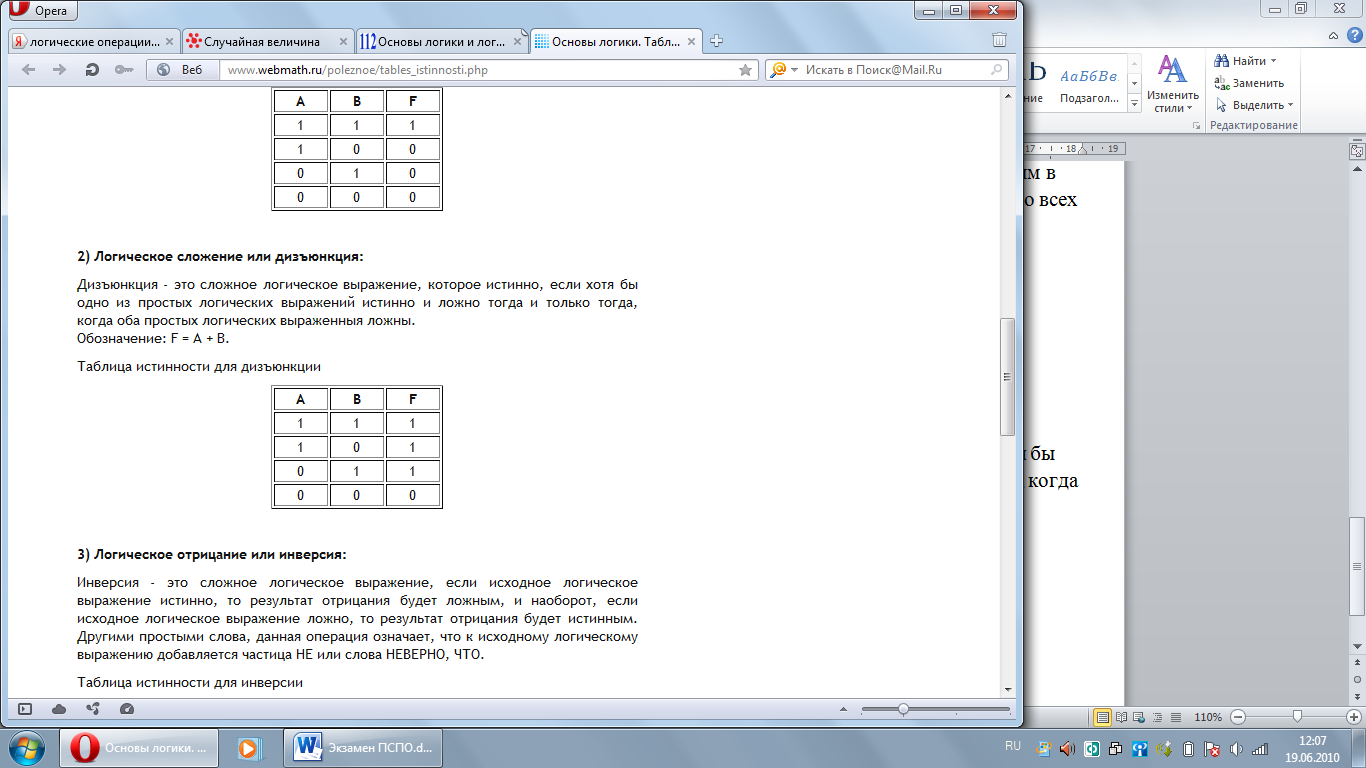
Таблица истинности для дизъюнкции.
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
![]()
Таблица истинности для инверсии.
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
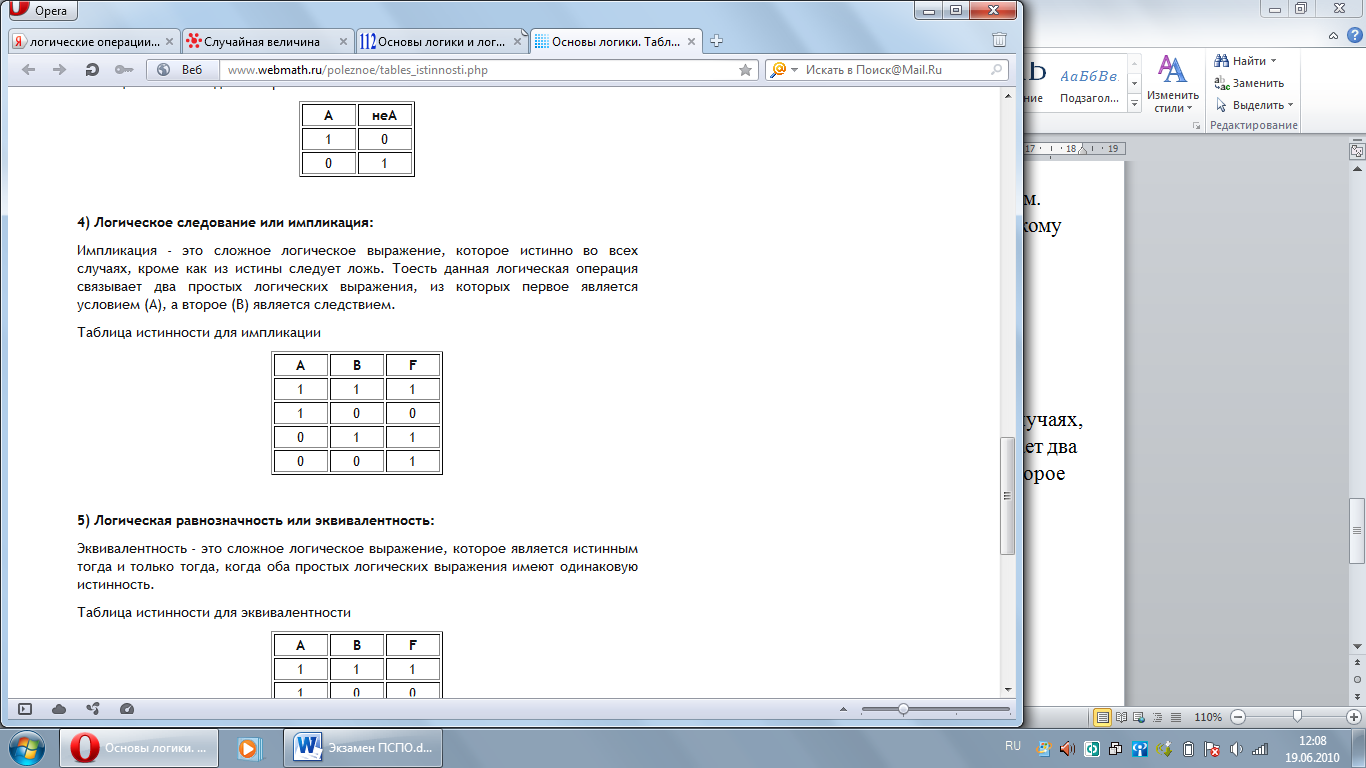
Таблица истинности для импликации.
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
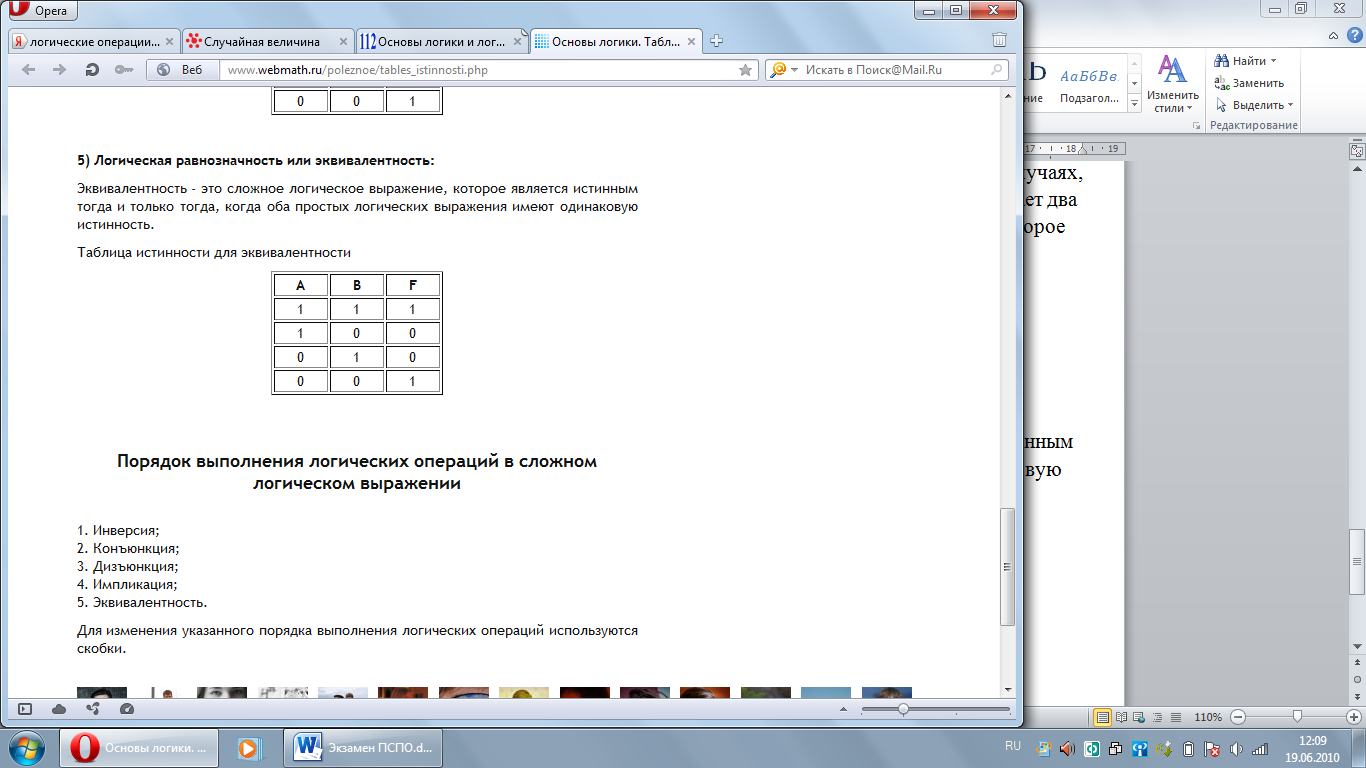
Таблица истинности для эквивалентности.
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
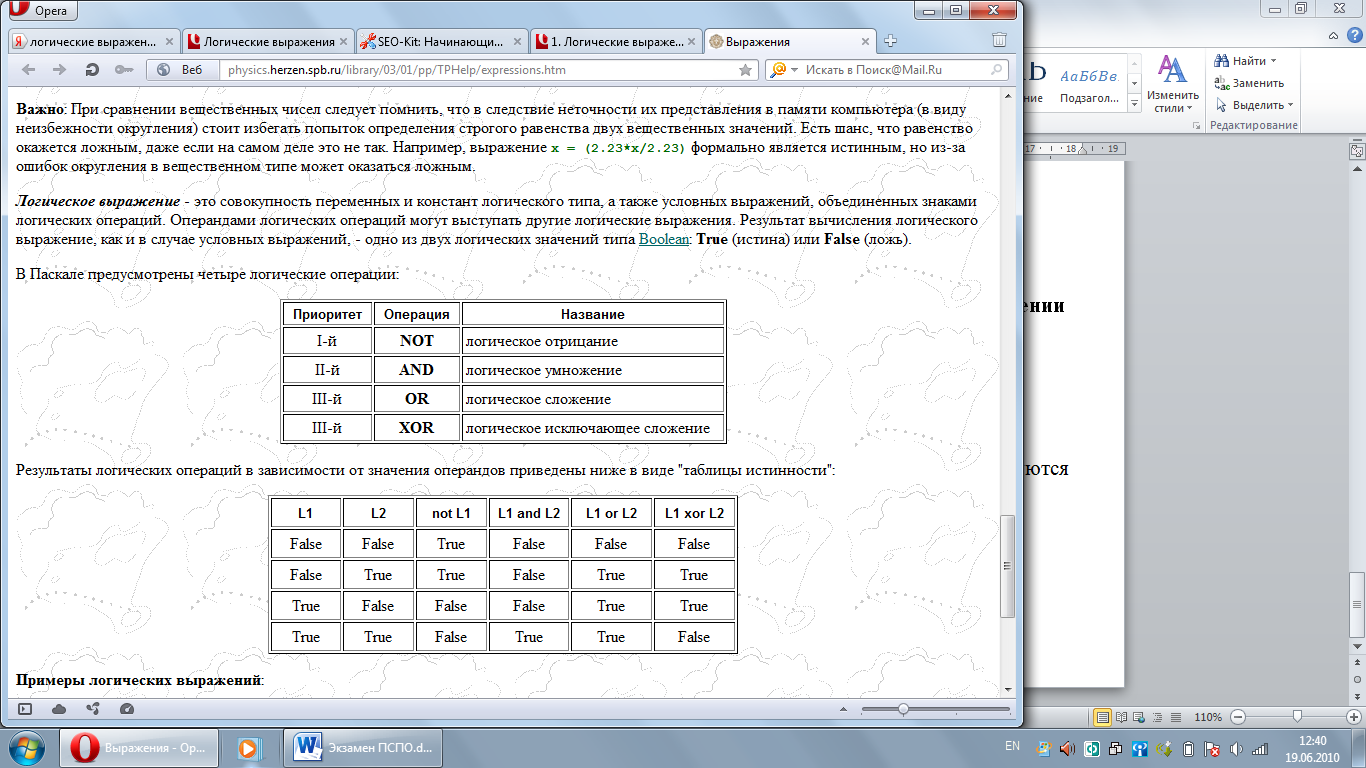
Результаты логических операций в зависимости от значения операндов приведены ниже в виде "таблицы истинности":

Шесть операций сравнения (все они относятся к четвертому (низшему) приоритету):

Необходимо заключать в скобки условные выражения, выступающие операндами логических операций. Это необходимо сделать для того, чтобы сначала выполнялись операции сравнения (они имееют самый низший приоритет), а лишь затем логические операции.
