29. Производственная функция Кобба-Дугласа. Эластичность объема производства.

производственную функцию Кобба-Дугласа.

Y = AK^αL^1-α,

где Y – объем производства, К – затраты капитала, L – затраты труда.

Полученная формула является частным случаем более общей формулы:

Y = AK^αL^β.

Учитывая влияние случайных возмущений, свойственных любому экономическому процессу, функция Кобба-Дугласа запишется следующим образом:

Y = AK^αL^βε.

Путем логарифмирования обеих частей данную степенную модель можно свести к линейной:

lnY = lnA + α·lnK + β·lnL + lnε.

Переходя к новым переменным Y'=lnY, A'=lnA, K'=lnK, L'=lnL, ε'=lnε, получаем линейную регрессионную модель:

Y' = A' + α·K' + β·L' + ε'.

Эластичность выпуска продукции.

Показатели α и β являются коэффициентами частной эластичности·объема производства Y соответственно по затратам капитала К и труда L. Это означает, что с увеличением только затрат капитала (труда) на 1% объем производства возрастает на α% (β%):

;

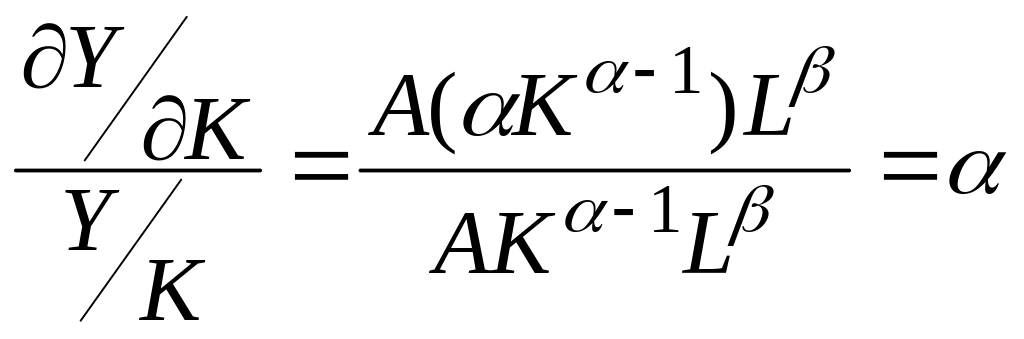30. Производственная функция Кобба-Дугласа. Эффект от масштаба производства.

Где y - объем производства,

K- затраты капитала

H – затраты труда

a, - параметры.

Путем логарифмирования обеих частей уравнения данную степенную модель можно свести к линейной:

Переходим к новым переменным:

L(штрих)

Эластичность выпуска продукции

Показатели и y по затратам капитала K и труда L. Это означает, что с увеличением только затрат капитала /труда на 1% V производства возрастает на

= =

Вывод:

При изменении только затрат капитала на 1% объем производства в среднем изменится на

При изменении только затрат труда на 1% объем производства в среднем изменится на

Эффект от масштаба производства

Если в сумме превышает 1, то говорят, что функция имеет возрастающий эффект от масштаба производства. Это означает, что если K и L увеличиваются в некоторой пропорции, то y растет в большей пропорции. Если сумма равна 1, то говорят о постоянном эффекте от масштаба производства, если сумма <1, то имеет место убывающий эффект от масштаба производства.

Пусть K и L увеличиваются в 2 раза. Найдем новый уровень выпуска y*

y*=

Если >1, то y увеличивается больше, чем в 2 раза, если , то y поднимается в 2 раза.

Т.к. Кобб и Дуглас предлагали постоянную отдачу от машстаба производства, то было сделано допущение , тогда функция К-Д примет вид y= , тогда прологарифмируем обе части данного уравнения ,

Где ln a= , ; = ,

, Перейдем к

тогда логарифм приведем к линейному виду:

31. Модели с распределенным лагом. Интерпретация параметров. Средний лаг. Медианный лаг.

При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени t-1,t-2…t-l. Величину l, характеризующую запаздывание в воздействии фактора на результат, в эконометрике называют лагом, а временные ряды самих факторных переменных - лаговыми переменными.

Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели наз-ся моделями с распределенными лагами вида:

Также существует модель авторегрессии. Например, потребление в момент времени t формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления в период t-1. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной. Эта модель вида:

Общий вид модели с распределенным лагом:

(максимальная величина лага конечна)

Если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значение переменной y в течение l следующих моментов времени.

Коэффициент регрессии при переменной характеризует среднее абсолютное изменение при изменении на 1 ед. в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Этот коэффициент наз-ют краткосрочным мультипликатором.

В момент времени t совокупное воздействие факторной переменной составит ( у.е., в момент времени t+l это воздействие можно охарактеризовать суммой =b – долгосрочным мультипликатором.

, где 0<j<1 и

В этом случае относительные коэффициенты являются весами для соответствующих коэффициентов . Каждый из них измеряет долю общего изменения результативного признака в момент времени t+j.

Средний лаг : (представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t.

Медианный лаг: (это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат).