12 Тест Голдфелда—Квандта.

Этот тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами.

Предположим, что средние квадратические (стандартные) отклонения возмущений σ_i пропорциональны значениям объясняющей переменной X (это означает постоянство часто встречающегося на практике относительного (а не абсолютного, как в классической

модели) разброса возмущений ε_i, регрессионной модели.

Упорядочим п наблюдений в порядке возрастания значений регрессора X и выберем т первых и т последних наблюдений.

В этом случае гипотеза о гомоскедастичности будет равносильна тому, что значения e₁,…,e_m и e_n-m+1,…e_n (т. е. остатки в, регрессии первых и последних т наблюдений) представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии.

Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей, как известно (см., например, [12]), проверяется с помощью критерия Фишера—Снедекора. Нулевая гипотеза о равенстве дисперсий двух наборов по т наблюдений (т. е. гипотеза об отсутствии гетероскедастичности) отвергается, если

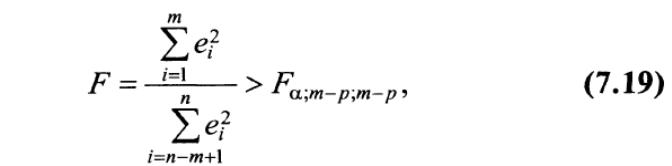
где р — число регрессоров.

Заметим, что числитель и знаменатель в выражении (7.19) следовало разделить на соответствующее число степеней свободы, но в данном случае эти числа одинаковы и равны {т— р).

Мощность теста, т. е. вероятность отвергнуть гипотезу об отсутствии гетероскедастичности, когда действительно гетероскедастичности нет, оказывается максимальной, если выбирать т порядка п/3.

При применении теста Голдфелда—Квандта на компьютере нет необходимости вычислять значение статистики F вручную, так как величины и представляют собой суммы квадратов остатков регрессии, осуществленных по «урезанным» выборкам.

13. Тест Уайта. Тест ранговой корреляции Спирмена и тест Голдфелда—Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.

Очевидно, для продвижения к этой цели необходимы некоторые дополнительные предположения относительно характера гетероскедастичности. В самом деле, без подобных предположений, очевидно, невозможно было бы оценить п параметров {п дисперсий ошибок регрессии σ_i²) с помощью п наблюдений. Наиболее простой и часто употребляемый тест на гетероскедастичность — тест Уайта. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же ф у н к ц и ю от наблюдаемых значений регрессоров, т.е.

σ_i² = f (x_i),i=1,…,n. (7.20)

Чаще всего функция/выбирается квадратичной, что соответствует тому, что средняя квадратическая ошибка регрессии зависит от наблюдаемых значений регрессоров приближенно линейно. Гомоскедастичной выборке соответствует случай f = const. Идея теста Уайта закшочается в оценке функции (7.20) с помощью соответствующего уравнения регрессии для квадратов остатков:

е_n² =fx(_i)-u_i , i= 1,..., n, (7.21)

где u_i — случайный член.

Гипотеза об отсутствии гетероскедастичности (условие f= const) принимается в случае незначимости регрессии (7.21) в целом.

В большинстве современных пакетов, таких, как «Econometric Views», регрессию (7.21) не приходится осуществлять вручную — тест Уайта входит в пакет как стандартная подпрограмма. В этом случае функция f выбирается квадратичной, регрессоры в (7.21) — это регрессоры рассматриваемой модели, их квадраты и, возможно, попарные произведения.

15. Обобщенная линейная модель множественной регрессии. Понятие автокорреляции. Тесты на наличие автокорреляции: их преимущества и недостатки. Обобщенная линейная модель множественной регрессии предполагает следующую систему соотношений и условий: 1)     ;

.

Ранг неслучайной (детерминированной) матрицы Х предполагается равным p + 1 < n, p — число предикторов,  случайный вектор, n — число наблюдений; 2)  - где  — матрица размера nґn состоящая из нулей. 3) , где  — положительно определенная матрица. Это означает, что определители всех главных миноров матрицы  положительны. Напомним, что главными минорами матрицы  являются миноры вида: 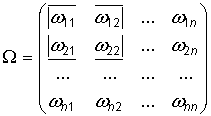. Итак, в обобщенной линейной регрессионной модели дисперсии и ковариации ошибок наблюдений могут быть произвольными. Доказано, что при применении обычного МНК для построения оценок коэффициентов в условиях обобщенной модели получается смещенная оценка ковариационной матрицы . Поэтому, оценки коэффициентов модели полученные по методу МНК будут несмещенными, состоятельными, но не эффективными. Для получения эффективных оценок нужно использовать оценки коэффициентов полученных на основе других методов, например, на основе обобщенного метода наименьших квадратов ОМНК. Автокорреляция. Если прослеживается влияние результатов предыдущих наблюдений на результаты последующих, случайные величины (ошибки) ε_i в регрессионной модели не оказываются независимыми, т.е. не выполняется вторая часть третьей предпосылки регрессионного анализа. Такие модели называются моделями с наличием автокорреляции. Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними уровнями ряда можно определить с помощью теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле: . В конце каждого учебника приведены математико-статистические таблицы, среди них таблица критерия Дарбина-Уотсона. По таблице на пересечении соответствующего числа наблюдений и числа объясняющих переменных находим пороговые значения d_в и d_н.

На ось d наносятся шесть значений:

___________________________________________________________ d

0 d_н d_в 4-d_в 4-d_н 4

Если расчетное значение:

0< d <d_н, то принимается альтернативная гипотеза о наличии положительной автокорреляции;

d_н< d <d_в, или 4-d_в< d <4-d_н, то вопрос об отвержении или принятии гипотезы остается открытым;

d_в< d <4-d_в, то гипотеза об отсутствии автокорреляции не отвергается (принимается);

4-d_н< d <4, то принимается альтернативная гипотеза о наличии отрицательной автокорреляции.

Наряду с тестом Дарбина-Уотсона для проверки наличия автокорреляции используются тестом Бреуша-Годфри.

Тест серий Бреуша-Годфри основан на предположении, что если между соседними наблюдениями имеется корреляция, то в уравнении:

e_t = ρe_t-1 + ν_t, (t = 1, …, n)

коэффициент ρ окажется значимо отличным от нуля (здесь e_t – остатки регрессии, полученной обычным МНК).

Преимущество теста Бреуша-Годфри заключается в том, что он позволяет выявить корреляцию между более отдаленными наблюдениями, тогда как тест Дарбина-Уотсона выявляет корреляцию только между соседними уровнями и содержит зону неопределенности.

Наиболее распространенным приемом устранения автокорреляции во временных рядах является построение авторегрессионных моделей.