4. Изображение по Лапласу функции равно

1:

5. Единичная функция обладает фильтрующим действием:

16. Переходная и импульсная переходная функции.

При подключении линейной электрической цепи (ЭЦ) с нулевыми начальными условиями (НУ) (в момент времени t=0) к источнику постоянного напряжения U между двумя какими – либо точками ЭЦ возникает напряжение u_ab(t), являющееся функцией времени и пропорциональное воздействующему напряжению U, рис.3:

Рисунок 3.

Df3: h(t) – переходная функция по напряжению. Это безразмерная величина, численно равная напряжению между точками a и b ЭЦ, если на ее вход подать постоянное напряжение в 1 вольт.

h(t) можно определить расчетным либо опытным путем.

Df4. Если на вход какой-либо ЭЦ в в момент времени t=0 к источнику постоянного напряжения U, тогда ток i(t) в любой ветви

Df5. g(t) – переходная проводимость, если U=1 В, то i(t)=g(t).

Рассмотрим случай, когда входное напряжение является дельта - функцией, т.е. U(t)=

Представим как сумму двух прямоугольных импульсов с амплитудой , один из которых возникает при t=0, другой – при t= , рис.4. Рисунок 4

Представление дельта - функции как суммы двух единичных функций.

Таким образом, для расчетов по напряжению

(1)

Df6. Дельта – функции в формуле (1) называется дельта – функцией по напряжению. Аналогично этому представлению можно представить дельта - функцию с помощью переходной проводимости

(2)

Df7. Дельта – функции в формуле (2) называется дельта – функцией по проводимости.

При t> и нулевых начальных условиях ток на входе цепи при воздействии на нее U(t)= будет равен

(3)

Разложим в ряд Тейлора в точке t:

Тогда из (3) получим: (4)

Df8. - импульсная переходная проводимость, численно равная току при t> при воздействии u(t)= .

Df9. Аналогично называется импульсной переходной функцией по напряжению. Она численно равна при t> напряжению на выходе четырехполюсника при воздействии на его вход U(t)=

17. Вывод формулы (интеграла) наложения.

Пусть дана ЭДС e(t) нелинейной формы, рис. 5.

Рисунок 5.

При Δτ реакция цепи на первый прямоугольный импульс равна реакции на дельта – функцию , умноженную на площадь этого импульса . Реакция на второй импульс - и т.д.

Тогда, для момента времени реакция цепи (5)

(5) – формула наложения.

18. Вывод формулы для интеграла Дюамеля.

Интеграл Дюамеля – та же формула наложения, но полученная на основе суммирования не дельта, а единичных функций, рис.6.

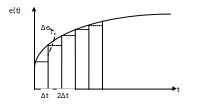
Рисунок 6.

На рисунке 6 ЭДС e(t) представлена суммой единичных функций с шагом Δτ.

Реакция цепи на первую ступень равна реакции на единичную функцию g₁(t), умноженную на высоту первой ступени:

Реакция цепи на вторую ступень равна реакции на единичную функцию g₁(t), умноженную на высоту второй ступени:

Тогда, для получим:

(6)

(6) – интеграл Дюамеля.

Интеграл Дюамеля целесообразно применять в тех случаях, когда известны или легко находятся реакции цепи на единичную функцию, ЭДС имеет кусочно-аналитическую форму.

19. Анализ переходных процессов операторным методом. Сущность операторного метода.

Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением.

В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

Изображение заданной функции определяется в соответствии с прямым преобразованием Лапласа:

.

(1)

В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

или

.

Следует отметить, что если оригинал увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.