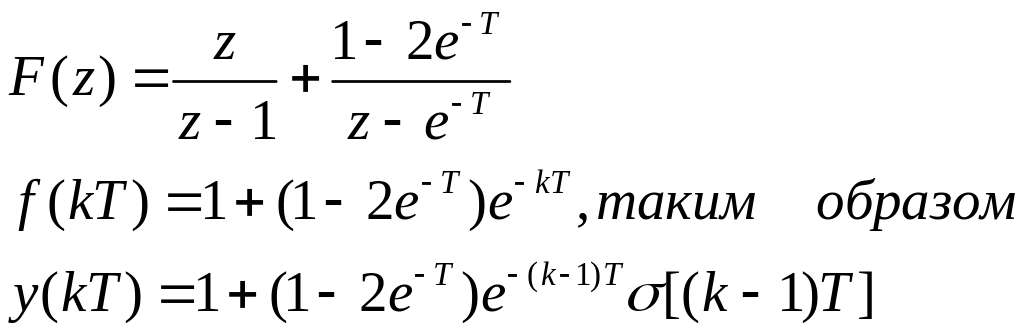- •1.Дискретные переменные. Понятие системы с дискретным временем.
- •2. Описание дискретных систем. Реализация операций интегрирования и дифференцирования конечными разностями
- •3 . Описание дискретных систем.
- •4. Разностные уравнения в переменных состояния и их решение.
- •5. Дискретное преобразование Лапласа. Определение z-преобразования. Теоремы z-преобразования.
- •6. Теоремы z-преобразований.
- •13. Построение схем моделирования в канонической форме
- •15. Изображение дискретных систем с помощью графов.
- •16. Понятие импульсной системы.
- •17. Математическое описание устройства выборки-хранения.
- •18. Свойства преобразования со звёздочкой
- •19. Преобразование спектра сигнала идеальным квантователем.
- •21. Передаточная функция импульсной системы
- •22. Передаточная функция импульсной системы с 1 квантователем 2 непрерывными звеньями
- •23. Передаточная ф-ция импульсной системы с двумя квантователями.
- •2 4. Передаточная функция разомкнутой импульсной системы с цифровым регулятором.
- •25. Пф замкнутой импульсной системы.
- •26. Порядок определения пф в общем случае.
- •27. Пф замкнутой импульсной системы с цифровым регулятором
- •28. Передаточная функция импульсной системы с внутренним контуром.
- •29. Описание импульсных систем переменными состояниями.
- •30. Построение дискретной модели в пс на основе непрерывной модели.
- •31. Анализ устойчивости дискретной системы по расположению полюсов на z-плоскости.
- •32. Отображение p-плоскости на z-плоскость
- •33. Критерий Джури
- •34. Анализ устойчивости по дискретной модели в пс
- •35. Билинейное преобразование. Отображение z-плоскости на w-плоскость.
- •36. Применение критерия Раусса для анализа устойчивости дискретной системы
- •37. Применение критерия Гурвица для анализа устойчивости дискретной системы
- •38. Анализ устойчивости дискретной системы с помощью частотных критериев. Критерий Найквиста.
- •39. Частотные характеристики импульсных систем.
- •43. Реализация цифрового пи-регулятора.
- •44. Реализация цифрового пд-регулятора.
- •45. Синтез цифрового пид-регулятора
21. Передаточная функция импульсной системы
W0(p) – ПФ непрерывной части системы.
Отнесём
экстраполятор к непрерывному объекту
и обозначим
![]() тогда
тогда
![]() в
соответствии со свойствами преобразования
со звёздочкой
в
соответствии со свойствами преобразования
со звёздочкой
![]() применим
данную формулу к выражению в квадратных
скобках
применим
данную формулу к выражению в квадратных
скобках![]()
Согласно
свойству преобразования со звездочкой
![]() тогда
тогда
![]() переходя к z-преобразованиям
переходя к z-преобразованиям
![]() где W(z)
– ПФ импульсной системы. ПФ W(z)
связывает в z-преобразованиях
вых. Сигнал со входным в момент квантования.
Выражение
носит общий характер если есть любая
функция, которую можно записать в виде
A(p)=B(p)F*(p)
то можно записать A*(p)=B*(p)F*(p)
или A(z)=B(z)F(z)
где W(z)
– ПФ импульсной системы. ПФ W(z)
связывает в z-преобразованиях
вых. Сигнал со входным в момент квантования.
Выражение
носит общий характер если есть любая
функция, которую можно записать в виде
A(p)=B(p)F*(p)
то можно записать A*(p)=B*(p)F*(p)
или A(z)=B(z)F(z)
П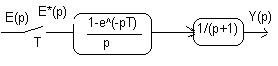 ример
W0(p)=1/(p+1)
Определить y(kT)
при единичном входном воздействии.
ример
W0(p)=1/(p+1)
Определить y(kT)
при единичном входном воздействии.
1,
Выходные переменные Y(p)=W(p)E*(p)
где W(p)=![]() или
Y(z)=W(z)E(z)
или
Y(z)=W(z)E(z)
2. По таблицам для единичной ф-ции E(z)=z/(z-1)
3.
Находим W(z)
принимаем F*(p)=1-e-pT
B(p)=![]() ;
W(p)=B(p)F*(p)
W(z)=B(z)*F(z)
F(z)=F(p)=1-z
-1=(z-1)/z
B(z)=z{
}=
;
W(p)=B(p)F*(p)
W(z)=B(z)*F(z)
F(z)=F(p)=1-z
-1=(z-1)/z
B(z)=z{
}=![]() -по
таблице. Тогда
-по
таблице. Тогда
![]() 4, Опр Z-преобразование
вых. Переем.
4, Опр Z-преобразование
вых. Переем.
![]() 5
5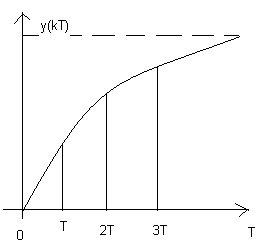 Выполняем обратное z-преобразование
Выполняем обратное z-преобразование
![]() Раскладываем
на простые дроби
Раскладываем
на простые дроби
![]()
![]() По
таблицам находим y(kT)=1-e
–kT
По
таблицам находим y(kT)=1-e
–kT
Выходная ф-ция представляет собой числовую последовательность и определена только в моменты выборки
22. Передаточная функция импульсной системы с 1 квантователем 2 непрерывными звеньями

ПФ экстраполятора содержит только звено W2(p)
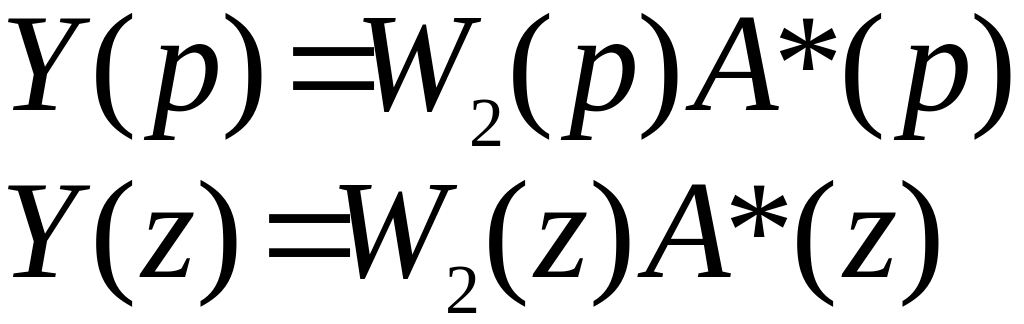
![]()
Применим
дискретное преобразование
Данное
выражение позволяет найти выходной
сигнал при заданном входном воздействии.
Однако из полученного выражения нельзя
получить отношение
![]() ,
т.е. ПФ сисетмы. Все полученные формулы
позволяют найти реакцию рассмотренных
систем на заданное входное воздействие.Пример:
,
т.е. ПФ сисетмы. Все полученные формулы
позволяют найти реакцию рассмотренных
систем на заданное входное воздействие.Пример:
 E(kT)
– определяет единичную функцию Определить
y(kT)
E(kT)
– определяет единичную функцию Определить
y(kT)

Для
объекта с экстраполятором
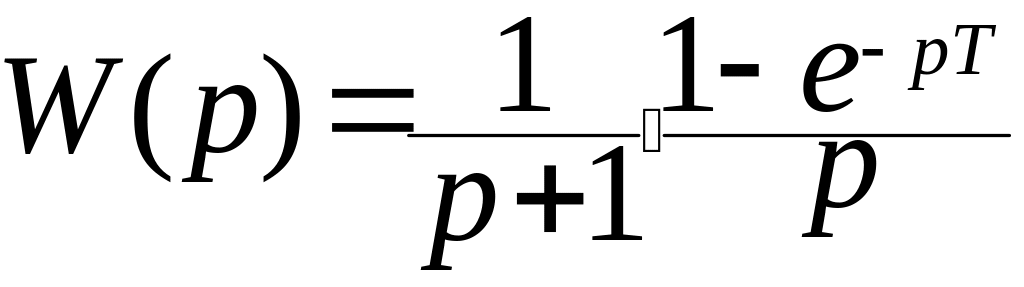
Пусть:
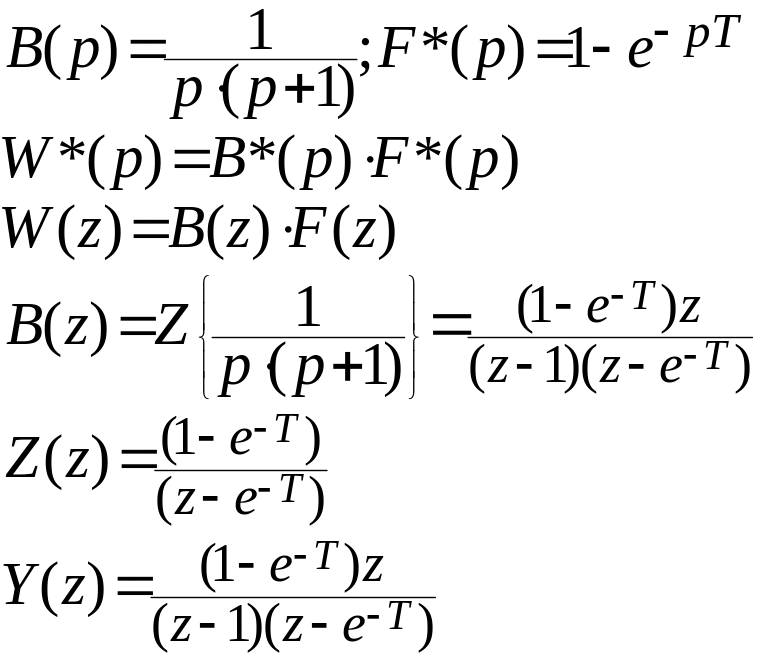
Выполняется обратное z-преобразование
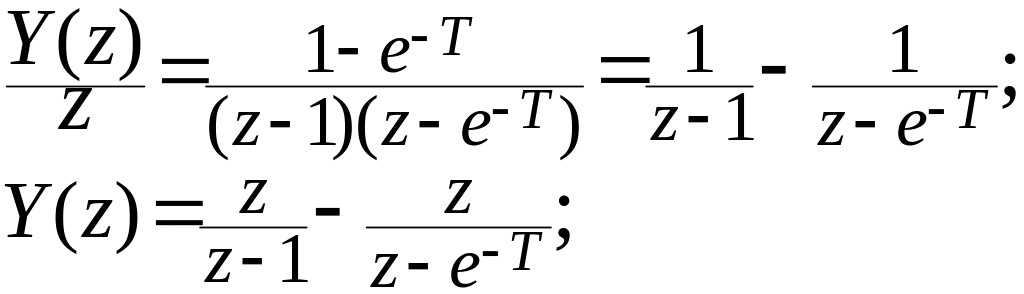
Выполняется
обратное z-преобразование
с помощью таблицы
![]()
23. Передаточная ф-ция импульсной системы с двумя квантователями.
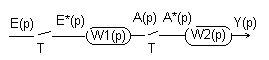 Оба
квантователя обезательно должны иметь
одинаков период квантования. W1(p)
и w2(p)
– ПФ непр. Звеньев, содержащие
экстрополяторы.
Y(p)=w2(p)A*(p);Y(p)=w2(p)A(p);A(p)=w1(p)E*(p);A(z)=w1(z)w2(z)E*(z)
общая передаточная ф-ция равна произведению
передаточных ф-ций импульсных систем.
W(z)=W1(z)*W2(z)
Оба
квантователя обезательно должны иметь
одинаков период квантования. W1(p)
и w2(p)
– ПФ непр. Звеньев, содержащие
экстрополяторы.
Y(p)=w2(p)A*(p);Y(p)=w2(p)A(p);A(p)=w1(p)E*(p);A(z)=w1(z)w2(z)E*(z)
общая передаточная ф-ция равна произведению
передаточных ф-ций импульсных систем.
W(z)=W1(z)*W2(z)
ПФ импульсной системы с послед. Соед. Непр. Звеньев
В этом случае экстрополятор содержит только звено w1
 Y(p)=W1(p)*W2(p)E*(p)
Y(z)=
Y(p)=W1(p)*W2(p)E*(p)
Y(z)=![]() -
z-ПФ
импульс системы
-
z-ПФ
импульс системы
 В
этом случае экстрополятор содержит
второе звено Y(p)=W2(p)A*(p)
или Y(z)=W2(z)A(z)
A(p)=W1(p)E(p)
Принимаем Z-преобразование
В
этом случае экстрополятор содержит
второе звено Y(p)=W2(p)A*(p)
или Y(z)=W2(z)A(z)
A(p)=W1(p)E(p)
Принимаем Z-преобразование
![]()
![]() Из полученого выражения нельзя выразить
отношение Y(z)/E(z)
следовательно в данном случае передаточную
ф-цию. получить нельзя но полученное
выражение позволяет найти выходную
числовую последовательность если задано
входное воздействие
Из полученого выражения нельзя выразить
отношение Y(z)/E(z)
следовательно в данном случае передаточную
ф-цию. получить нельзя но полученное
выражение позволяет найти выходную
числовую последовательность если задано
входное воздействие
2 4. Передаточная функция разомкнутой импульсной системы с цифровым регулятором.
Цифровой
регулятор является дискретным звеном
с ПФ Wp(z)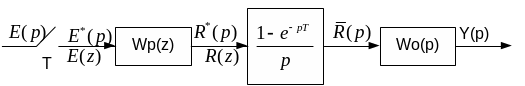
Для
регулятора
![]() или
или
![]() Выходной сигнал
Выходной сигнал
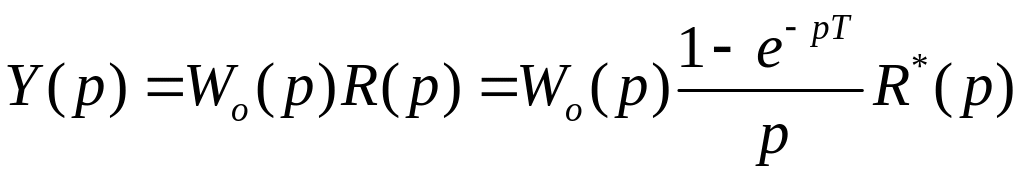 Находим
Находим

![]() Пример:ПФ
объекта
Пример:ПФ
объекта
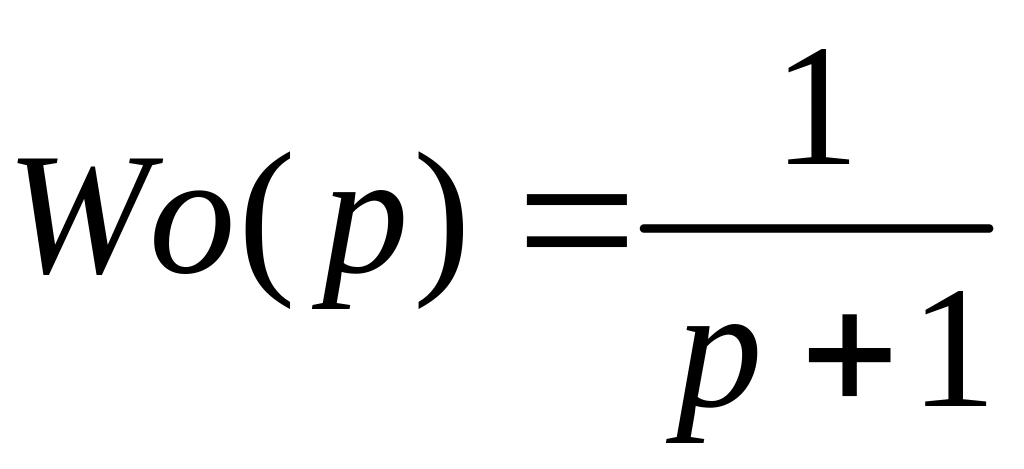 ,
Ур-е регулятора
,
Ур-е регулятора![]()
Найти Z-ПФ системы и реакцию на еденичное воздействие.
Применяем Z-преобразование к Ур-ю регулятора
![]() ,
тогда
,
тогда
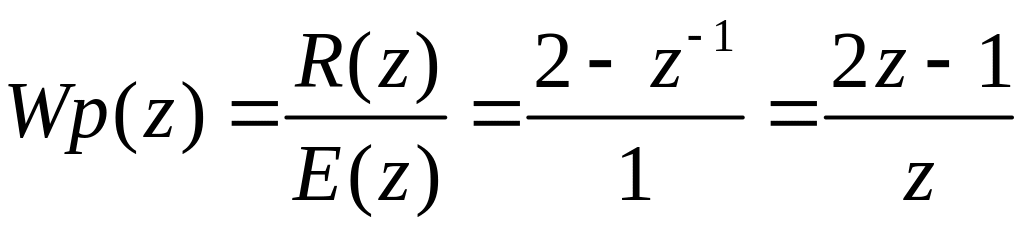
Находим Z-ПФ объекта с экстрополятором
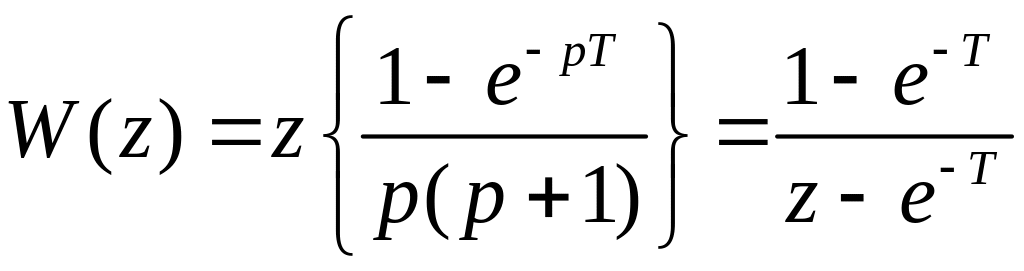
3.Находим
Z-преобразование
выходной переменной
![]()
4.Находим
z-преобразование
выходной переменной
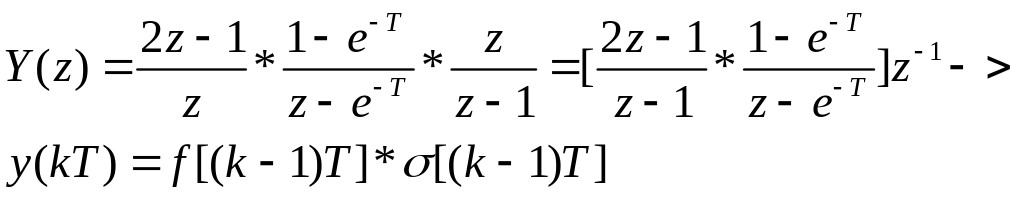
5.
Выполняем обратное z-преобразование
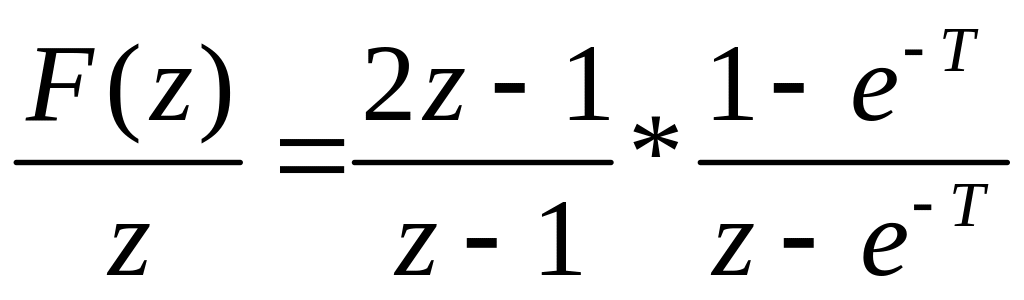
Раскладываем
на простые дроби