
- •1.Дискретные переменные. Понятие системы с дискретным временем.
- •2. Описание дискретных систем. Реализация операций интегрирования и дифференцирования конечными разностями
- •3 . Описание дискретных систем.
- •4. Разностные уравнения в переменных состояния и их решение.
- •5. Дискретное преобразование Лапласа. Определение z-преобразования. Теоремы z-преобразования.
- •6. Теоремы z-преобразований.
- •13. Построение схем моделирования в канонической форме
- •15. Изображение дискретных систем с помощью графов.
- •16. Понятие импульсной системы.
- •17. Математическое описание устройства выборки-хранения.
- •18. Свойства преобразования со звёздочкой
- •19. Преобразование спектра сигнала идеальным квантователем.
- •21. Передаточная функция импульсной системы
- •22. Передаточная функция импульсной системы с 1 квантователем 2 непрерывными звеньями
- •23. Передаточная ф-ция импульсной системы с двумя квантователями.
- •2 4. Передаточная функция разомкнутой импульсной системы с цифровым регулятором.
- •25. Пф замкнутой импульсной системы.
- •26. Порядок определения пф в общем случае.
- •27. Пф замкнутой импульсной системы с цифровым регулятором
- •28. Передаточная функция импульсной системы с внутренним контуром.
- •29. Описание импульсных систем переменными состояниями.
- •30. Построение дискретной модели в пс на основе непрерывной модели.
- •31. Анализ устойчивости дискретной системы по расположению полюсов на z-плоскости.
- •32. Отображение p-плоскости на z-плоскость
- •33. Критерий Джури
- •34. Анализ устойчивости по дискретной модели в пс
- •35. Билинейное преобразование. Отображение z-плоскости на w-плоскость.
- •36. Применение критерия Раусса для анализа устойчивости дискретной системы
- •37. Применение критерия Гурвица для анализа устойчивости дискретной системы
- •38. Анализ устойчивости дискретной системы с помощью частотных критериев. Критерий Найквиста.
- •39. Частотные характеристики импульсных систем.
- •43. Реализация цифрового пи-регулятора.
- •44. Реализация цифрового пд-регулятора.
- •45. Синтез цифрового пид-регулятора
17. Математическое описание устройства выборки-хранения.


Сигнал на выходе устройства может быть представлен в виде:
 (1)
(1)
Изображение по Лапласу выходного сигнала с учётом теоремы запаздывания
 (2)
(2)
Первый
сомножитель в (2) не зависит от входного
сигнала
![]() поэтому его можно отнести к экстрополятору
и рассматривать как передаточную
функцию.
поэтому его можно отнести к экстрополятору
и рассматривать как передаточную
функцию.
Тогда
квантователь осуществляет преобразование
входного сигнала в соответствии с
выражением:
 (3) Данное выражение по определению
соответствует преобразованию Лапласа
дискретной функции
(3) Данное выражение по определению
соответствует преобразованию Лапласа
дискретной функции
![]() ,
оно называется преобразованием со
звёздочкой.
,
оно называется преобразованием со
звёздочкой.
Т .о.
устройство выборки-хранения можно
представить схемой из квантователя
периодом Т и экстрополятора:
.о.
устройство выборки-хранения можно
представить схемой из квантователя
периодом Т и экстрополятора:
Следует
иметь в виду, что выражение (3) не является
моделью реального квантователя. В
реальной системе сигнал
![]() отсутствует. Выражение
отсутствует. Выражение
 так же не является ПФ реального
экстрополятора, они получены искусственно,
путём математического преобразов.
выражения (1).Однако комбинация этих
элементов точно отображает соотношения
между входным и выходным сигналами для
реального устройства выборки-хранения.
Но использовать в схеме отдельно
квантователь или экстрополятор нельзя.
За квантователем обязательно должен
следовать экстрополятор и наоборот.Обратное
преобразование Лапласа для выражения
(3) даёт:
так же не является ПФ реального
экстрополятора, они получены искусственно,
путём математического преобразов.
выражения (1).Однако комбинация этих
элементов точно отображает соотношения
между входным и выходным сигналами для
реального устройства выборки-хранения.
Но использовать в схеме отдельно
квантователь или экстрополятор нельзя.
За квантователем обязательно должен
следовать экстрополятор и наоборот.Обратное
преобразование Лапласа для выражения
(3) даёт: Т.о.
Т.о.
![]() физически не реализуема, поэтому
устройство осуществляющее преобразов.
в соответствии с выражением (3) или (4)
называется идеальным квантователем.
Блок имеющий ПФ
физически не реализуема, поэтому
устройство осуществляющее преобразов.
в соответствии с выражением (3) или (4)
называется идеальным квантователем.
Блок имеющий ПФ
 называется экстрополятором 0-го порядка.
называется экстрополятором 0-го порядка.
18. Свойства преобразования со звёздочкой
Найдём преобразование со звёздочкой для единичной ступенчатой функции
![]() Аналогично
выражается для Z-преобразования
Аналогично
выражается для Z-преобразования
![]()
Таким образом преобразование со звёздочкой можно получить из Z-преобразований. E*(p)=E(z) при z=eTp
2)
E*(p)
является периодической функцией от p
с периодом jwp,
т.е. E*(p)=
E*(p+
jwp),
где n=0,
![]() ,
…
,
…
![]() - частота квантования
- частота квантования
3)
Если E(p)
имеет полюс p1,
то ф-ция E*(p)
будет иметь полюсы p1+mjwp
, где n=
0,
![]() ,
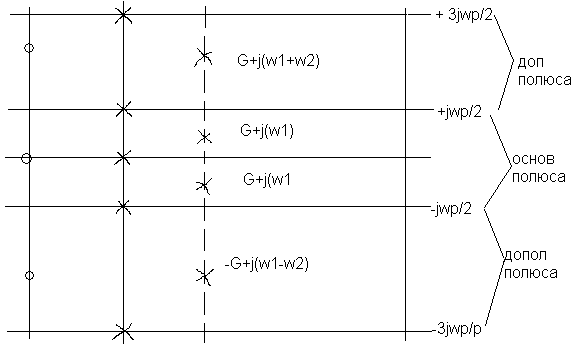
… Положение нулей E*(p)
также обладает периодичностью таким
образом, если известно расположение
нулей и полюсов E*(p)
в основной полосе частот – wp/2<w<wp/2,
то оно будет повторяться в дополнительных
полюсах
,
… Положение нулей E*(p)
также обладает периодичностью таким
образом, если известно расположение
нулей и полюсов E*(p)
в основной полосе частот – wp/2<w<wp/2,
то оно будет повторяться в дополнительных
полюсах
19. Преобразование спектра сигнала идеальным квантователем.
П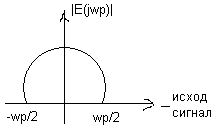
 усть
сигнал E(p)
подвергается квантованию.
усть
сигнал E(p)
подвергается квантованию.
W p-частота
квантованияИз приведенных рисунков
следует, что сигнал может быть полностью
восстановлен после квантования с помощью
идеального фильтра, если его спектр не
выходит за пределы основной полосы,
т.е. максим. Частота сигнала E(p)
должно быть меньше wp/2
в противном случае сигнал восстан. с
искажением. Таким образом для возможности
восстанавления квантованного сигнала
без искажения частота квантования
должна быть как минимум в два раза выше
max
частоты исходного сигнала.
p-частота
квантованияИз приведенных рисунков
следует, что сигнал может быть полностью
восстановлен после квантования с помощью
идеального фильтра, если его спектр не
выходит за пределы основной полосы,
т.е. максим. Частота сигнала E(p)
должно быть меньше wp/2
в противном случае сигнал восстан. с
искажением. Таким образом для возможности
восстанавления квантованного сигнала
без искажения частота квантования
должна быть как минимум в два раза выше
max
частоты исходного сигнала.
Блок имеющий ПФ Who(p)=(1- e-Tp)/p называется экстраполятором нулевого порядка.
Устройство вых. сигнал, которого описывается выражением
E*(p)=∑ε(kT)۰e-kTp называется идеальным квантователем.
Если мах частота входного сигнала < wp/2, то сигнал может быть полностью восстановлен после квантователя с помощью фильтра. Идеальный фильтр имеет коэффициент передачи в основной полосе u=0 за ее пределами. Если спектр входного сигнала выходит за пределы wp/2, то его нельзя восстановить с помощью идеального фильтра. Поэтому частота квантователя должна быть в 2 раза выше мах частоты входного сигнала.
Who(p)=(1- e-Tp)/p = T ۰ (sin(πw/wp))/( πw/wp)۰e-jπw/wp – частотная характеристика экстраполятора 0 – го порядка.
׀ Who׀=
T
۰
(sin(πw/wp))/(
πw/wp)
- АЧХ argWho=
-πw/wp
+
Ө
- ФЧХ
Who׀=
T
۰
(sin(πw/wp))/(
πw/wp)
- АЧХ argWho=
-πw/wp
+
Ө
- ФЧХ
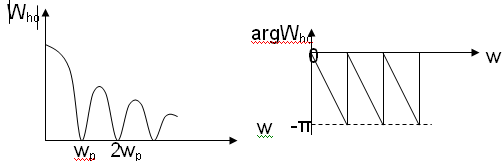
Пусть на вход системы поступает синусоидальный сигнал с частотой w1< wp/2, тогда на выходе квантователя и соответственно на входе экстраполятора мы получаем сигнал вида w1±nwp, где n=0,1,2… При прохождении через экстраполятор сигнал также будет иметь бесконечное число соответственно с ростом частоты их амплитуда будет уменьшатся.
