49. Вычисление описывающей функции на примере идеального реле

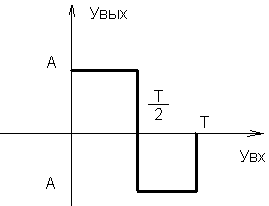
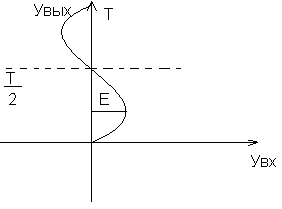
Т.к. выходная функция U(t) нечётная; то А1 = 0,

Учитывая, что получим

При ,

Т.о. N (E, ) =

Обозначение на структурной схеме:

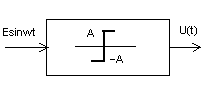или

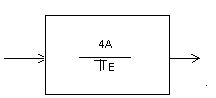
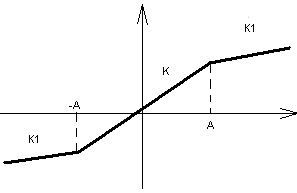
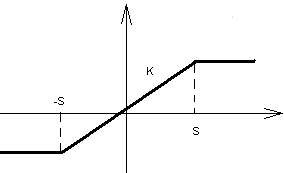
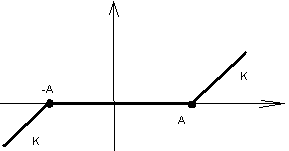
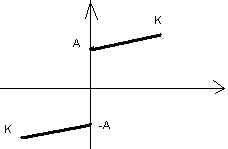
Таблица описывающих функций

Нелинейность	N (E, )
	К при E A K и - коэффициенты наклона характеристики
	К при Е A К
	0 при Е A К [1- ( )] при E>A
	0 при Е A При Е>A
	0 при Е A - при Е>1

50. Анализ устойчивости нелинейной сар с помощью описывающей функции.

Рассмотрим нелинейную систему

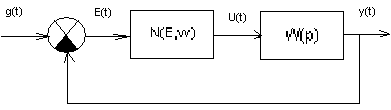
Представим в виды

=| |

Выходной сигнал нелинейного элемента

В нелинейной системе возникает предельный цикл (колебания с постоянной амплитудой), если выходной сигнал нелинейного элемента приблизительно sin-ый и полностью восстанавливается в замкнутом контуре, т.е. петлевой коэффициент усиления контура =1.

Т.о. необходимо определить знают ли значения Е и W при которых коэффициент усиления разомкнутого контура от входа нелинейного элемента к этой же точке по цепи ОС равен 1, т.е.

Предельный цикл возможен, если

или

Запишем полученное выражение в виде

Если при некоторых Е и данное уравнение выполняется, то предельный цикл в данной системе существует.

Поскольку в общем случае представляет собой комплексную величину, то уравнение нельзя решить относительно E и .

Решение можно осуществить графо-аналитическим методом.

Запишем уравнение в виде

Задаваясь значениями от 0 до + бесконечности строим на комплексной плоскости кривые соответствия левой и правой частям уравнения.

Если в какой-то точке кривые пересекутся, то можно будет предположить существование предельного цикла с параметрами, соответствующими данной точке.

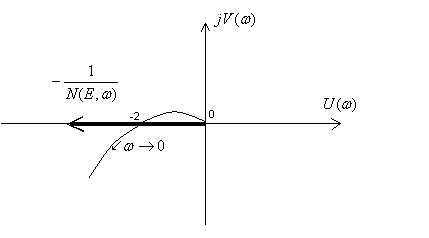
Пример:

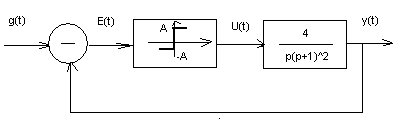
Для идеального реле

Тогда

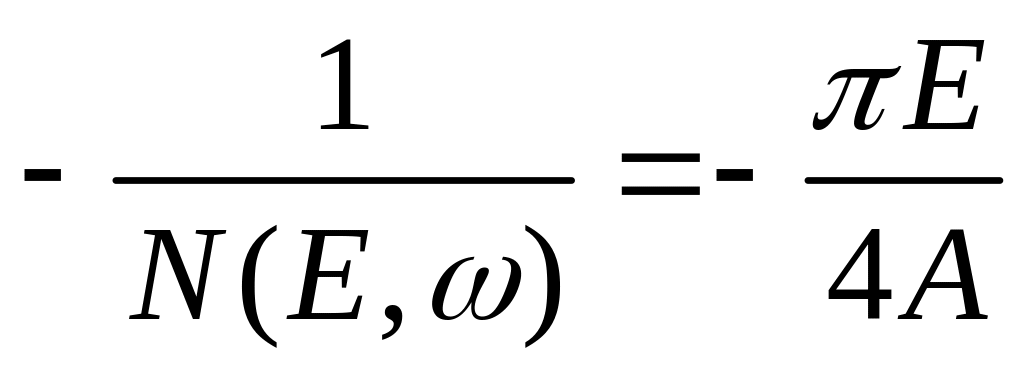
при Е=0

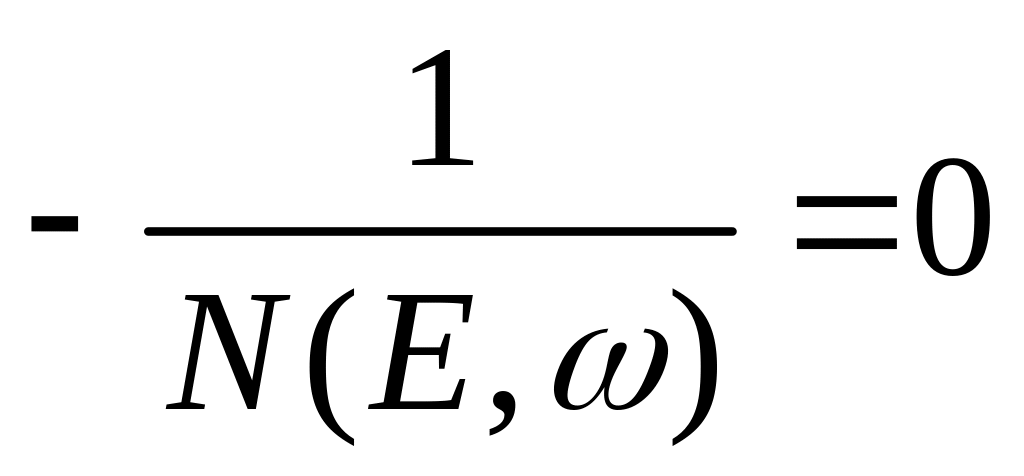
при

Для объекта

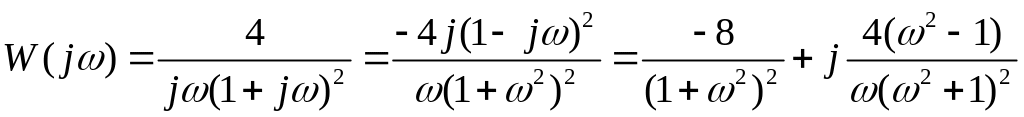
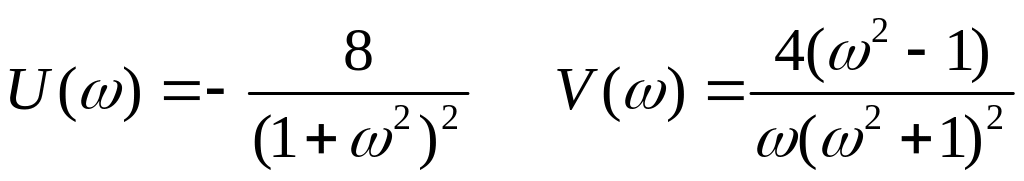
В системе возможен предельный цикл с параметрами

51. Устойчивость предельных циклов и её оценка с использованием описывающей функции.

В нелинейной системе существует два типа предельных циклов. В устойчивом предельном цикле амплитуда колебаний возвращается к своему прежнему значению после её изменения под действием возмущения и снятия этого возмущения. В устойчивом предельном цикле амплитуда колебаний после отклонения под действием возмущения и снятия этого возмущения либо продолжает возрастать, либо снижается до нуля.

Устойчивость предельного цикла можно оценить с помощью описывающих функций. Если в нелинейной системе нелинейное звено заменить пропорциональным звеном получим линейную систему

ПФ разомкнутой системы

Устойчивость данной системы можно оценить с помощью критерия Найквиста. Для устойчивости САР кривая G(jω) не должна охватывать точку (-1; j0) или кривая W(jω) не должна охватывать точку (-1/к; j0)

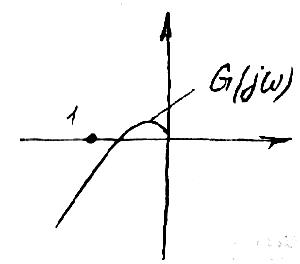
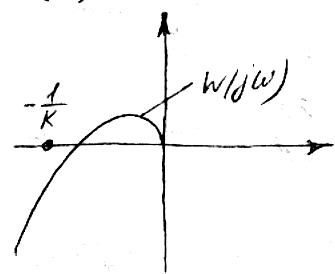При синтезе нелинейной системы возможно получение предельного цикла

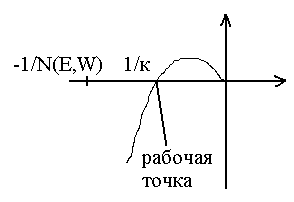
Параметры системы можно линеаризовать вблизи рабочей точки, соответствующей предельному циклу. При этом -1/N(E,W) заменится на -1/к.

Допустим, что амплитуда колебаний Е уменьшилась под действием возмущения, при этом и рабочая точка смещается вправо. По критерию Найквиста система становится неустойчивой, а в неустойчивой системе амплитуда колебаний возрастает, следовательно амплитуда колебаний восстановится. По определению в этом случае предельный цикл является устойчивым. Если бы при уменьшении Е рабочая точка сместилась влево, то система стала бы устойчивой и это бы привело к дальнейшему затуханию колебаний, следовательно предельный цикл был бы неустойчивый.