Интегрирование некоторых иррациональных алгебраических функций.

Пусть  рациональная функция своих аргументов. Тогда интеграл находится заменой переменных

Как правило, за берется наименьшее общее кратное чисел , где , т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.

Пример. Найти неопределенный интеграл .

Решение: Ясно, что . Учитывая это, делаем следующую замену переменных:

.

Интегрирование тригонометрических выражений.

Пусть - рациональная функция своих аргументов. Рассмотрим несколько случаев:

1й случай. Интеграл универсальной тригонометрической подстановкой сводится к интегралу от рациональной функции. При этом .

С учетом сделанной замены получим ,

где  рациональная функция, интеграл от которой рассматривался выше.

Пример: Найти неопределенный интеграл: .

Решение: Сделаем универсальную тригонометрическую подстановку:

; .

Тогда .

Последний интеграл вычислим отдельно. Для этого выделим полный квадрат в знаменателе дроби:

Воспользовавшись заменой переменной получим

Окончательно находим:

= = .

Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам.

2й случай. В интегралах , где и входят в подынтегральную рациональную функцию, только в четных степенях делается замена . При этом

.

Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида .

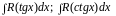Пример: Найти неопределенный интеграл:

.

Решение: Сделаем подстановку:

; .

Тогда

.

Пример. Найти неопределенный интеграл: .

Решение:

Интегрирование выражений вида

, (6)

где m и nцелые числа. Рассмотрим два случая:

1-й случай. Среди чисел m,n есть хотя бы одно нечетное. Тогда за t принимается функция, стоящая в основании другой степени.

Задача. Найти неопределенный интеграл:

.

Решение: Здесь функция sinx стоит в нечетной степени, поэтому

;

2-й случай. В выражении (6) оба числа m,n  четные неотрицательные.

Положим m=2p, n=2q и применим формулы:

.

Тогда

Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:

.

1.10 Определенный интеграл: задача о площади криволинейной трапеции

Задача.

Определение: Криволинейной трапецией называется фигура, ограниченная линейно x=a; x=b; y=0; y=f(x)0

Р азобьем основание криволинейной трапеции отрезок [a,b] на n частей точками a=x₀<x₁<x₂<…<x_n=b. Обозначим через x_i=x_i – x_i-1 длину i-го отрезка.

В каждом отрезке выберем произвольную точку

C_i [ x_i, x_i-1] и вычислим в ней значение функции f(C_i).

Заменим площадь i-й части криволинейной трапеции площадью прямоугольника с основанием и высотой f(C_i): ;

.

Причем равенство будет тем точнее, чем больше количество отрезков или чем меньше их длина.

1.11 Определение определенного интеграла.

Пусть функция y=f(x)определена на отрезке [a,b]. Разобьем отрезок [a,b] на части точками a=x₀<x₁<x₂<…<x_n=b. Обозначим через x_i=x_i – x_i-1 .

В каждом из отрезков возьмем точку C_i [ x_{i -1}, x_i] и вычислим в ней значение функции f(C_i). Составим интегральную сумму S_n= . Если существует предел интегральных сумм, при max x_i 0, которые не зависят от способа разбиения отрезка [a,b] на части и способа выбора точек C_i, то он называется определенным интегралом от a до b, от функции f(x) на dx. . Где a – нижний предел, b – верхний предел, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.

Теорема о существовании определенного интеграла.

Если функция y=f(x) непрерывна на отрезке [a,b], то существует определенный интеграл .

Замечание:

Определенный интеграл всегда является числом.

Определенный интеграл зависит от a, от b, от f(x) и не зависит от переменной интегрирования.

= = .

1.12Свойства определенного интеграла.

1
2		k-const
3
4		Т.к. длина отрезка =0
5
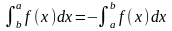
6
7	Если f(x) на [a;b], то
8	, где m значение f(x) на [a;b] – наименьшее M – наибольшее
9	Существует точка С  [a,b] такая, что

1.13Интеграл с переменным верхним пределом и его производная.

Интегралом с переменным верхним пределом называется интеграл от a до x по dx, где нижний предел число, а верхний предел – переменная интегрирования. . Геометрически это означает, что соответствующая площадь криволинейной трапеции будет переменной величиной.

Теорема: Производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывна). =f(x).

 Возьмем точку x и вычислим в ней значение функции J(x)= . Дадим x приращение x и вычислим значение функции. I(x+x)= _{= =}

Функция I(x) получает приращение I=I(x+x) – I(x)=

По теореме о среднем значении существует точка C (x,x+x), такая что = . Рассмотрим предел ,

т .к. при .

Из теоремы следует, что интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции.

1.14Формула Ньютона-Лейбница.

где F(x)-одна из первообразных f(x).

Рассмотрим , он является одной из первообразных f(x), т.е. , где C₀ – конкретное значение const. Найдем C₀. Подставим вместо верхнего предела x=a   C₀=-F(a)  . Подставим вместо верхнего предела x=b 

Формула позволяет вычислять определенный интеграл.

Пример: = = =

= = =

= =

1.15Интегрирование по частям и замена переменной в определенном интеграле.

Интегрирование по частям.

Например: = = =-1

Интегрирование с заменой переменной.

, где , .

Замечание: При замене переменной в определённом интеграле нужно поменять пределы интегрирования, причем решения уравнений и должны быть однозначными.

При замене переменной в определенном интеграле возвращаться к старой переменной не нужно.

Пример: = = = = =

1 .16Вычисление площади плоских фигур в декартовой системе координат.

Рассмотрим криволинейную трапецию, ограниченную прямыми x=a, x=b, y=0 и кривой y=f(x), где f(x)  0.

К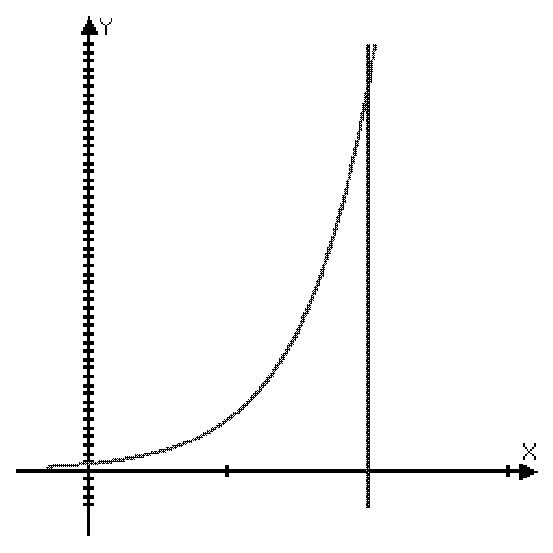 ак известно, площадь такой криволинейной трапеции выражается через определенный интеграл: S =

Пример: Вычислить площадь фигуры, ограниченной линиями y=e^2x, x=0, x=2, y=0. S= = = .

З амечание: Иногда криволинейную трапецию приходится разбивать на несколько частей. Площадь всей трапеции есть сумма площадей всех частей.

Пример: Вычислить площадь фигуры, ограниченной линиями y=x, xy=1(y=1/x), x=0, x=2, y=0. Разобьем трапецию на две части S₁ и S₂. Площадь всей трапеции: S=S₁+S₂= = = .

В общем случае площадь фигуры, ограниченной слева прямой x=a, справа прямой x=b, сверху кривой y=f₂(x),снизу кривой y=f₁(x), причем f₂(x)  f₁(x).

В этом случае, неважно, где лежит криволинейная трапеция, выше оси OX или ниже, или часть выше, часть ниже. Самое главное, чтобы выполнялось f₂(x)  f₁(x).

1.17 Вычисление площадей при параметрическом задании функции.

Пусть криволинейная трапеция ограничена линиями x=a, x=b, y=0, а верхняя граница задана параметрически . Как известно, площадь криволинейной трапеции равна S= = =S, так как dx=x(t)dt, f(x)=y(t). Причем нижний предел интегрирования t₁ соответствует точке x=a; x(t₁)=a, верхний предел интегрирования t₂ соответствует точке x=b; x(t₂)=b.

Пример: Вычислить площадь эллипса. Параметрические уравнения эллипса

В силу симметричности фигур вычислим 1/4 площади. Для этой части x меняется от 0 до a. Найдем пределы интегрирования.

0 = a cos t, cos t = 0, t₁=/2

a = a cos t, cos t = 1, t₂ = 0

Итак, =ab/4  S= ab (ед²).

1.18Полярная система координат.

Р ассмотрим на плоскости точку О, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью. Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа  - длина радиус-вектора |OM| и  - угол между радиус-вектором точки M и положительным направлением полярной оси.

Таким образом любая точка в полярной системе координат будет иметь две координаты M(,),  – полярный радиус,  – полярный угол. Очевидно, что  – величина неотрицательная (как длина любого вектора), а угол  может быть любой.

Если угол  измерен против часовой стрелки, то его будем считать положительным, если по часовой стрелке, то отрицательным.

Изображение линий в полярной системе координат.

= R – окружность с центром в полюсе и радиусом R.

=  - луч под углом к полярной оси .

=  – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла  и вычислять соответственно значения полярного радиуса . Если  получится меньше нуля, то картинки не будет (этой части рисунка не будет)

Спираль Архимеда	Кардиоида	трех лепестковая роза	окружность	Лемниската Бернулли
=	=1+cos 	=cos3	=4cos	2=cos2

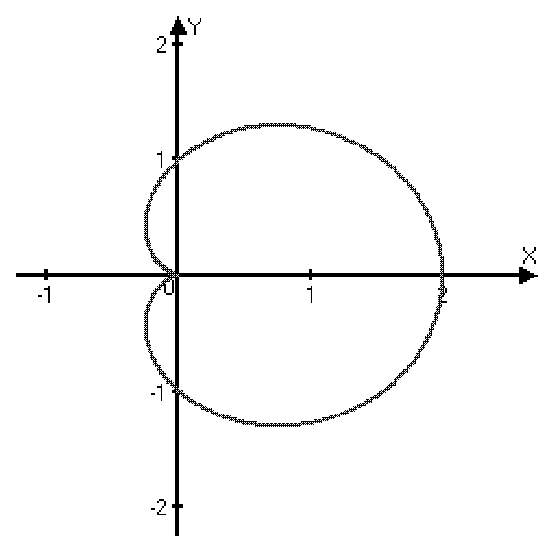
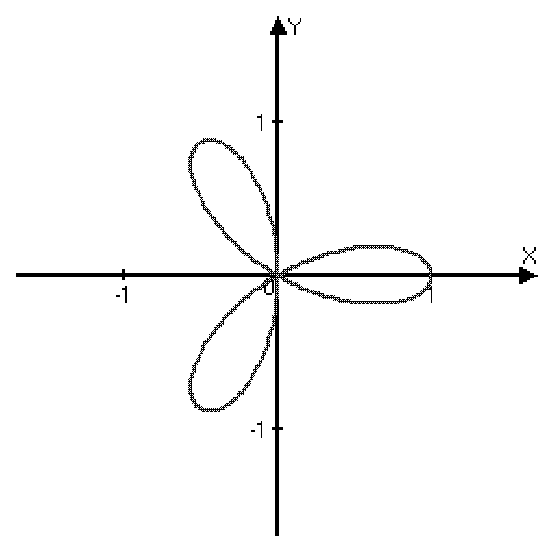
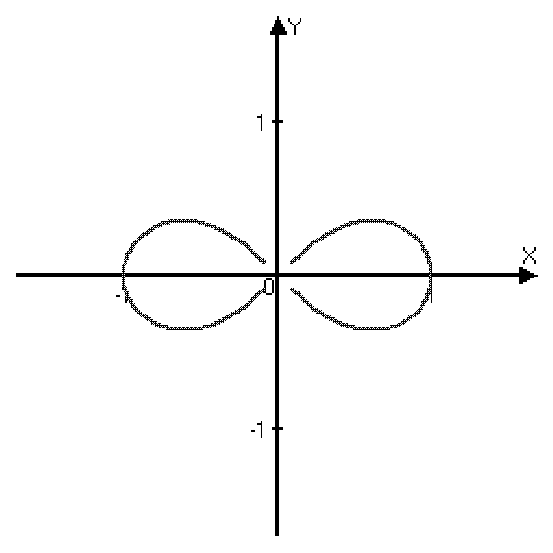
Связь между декартовой и полярной системами координат.

Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (; ) к декартовым (x; y):

, и от декартовых к полярным: ,

1.19Вычисление площади в полярной системе координат и кривой заданной параметрически.

Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора.

Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами  и  и кривой, заданной в полярной системе координат =().

Разобьем криволинейный сектор лучами = _i, i = 0…n на части =₀ <₁<₂<…<_n=

 =,  =,  =().

В каждой части произвольным образом выбираем точку C_i и вычисляем в ней значение _i =(C_i) угол i- части . Заменим площадь i- части площадью кругового сектора = = = =

Просуммируем площади всех круговых секторов .

Сумма этих площадей приближенно равна площади исходного криволинейного сектора. Причем, чем больше будет частей разбиения, тем меньше будет _i , тем точнее будет равенство.

В ПСК S= .

1.20Вычисление длины дуги кривой в декартовой системе координат.

Нужно вычислить длину плоской кривой L, заданной уравнением y=f(x) на отрезке [a,b].

Разобьем отрезок на части точками x_i где I=0…n, a=x₀<x₁<x₂<…<x_n=b.

Через эти точки проведем прямые параллельные оси OY, которые разобьют кривую на M частей. Выпишем в эти части ломанную.

Длина I-ого звена ломанной: l_i=

Просуммируем сумма длин звеньев ломанной приближенно равна длине кривой. Переходя к пределу: = =

Пример: Вычислить длину полукубической параболы , где , x=0, x=1. = = =

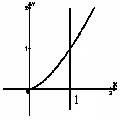
1.21Вычисление длины дуги в полярной системе координат и кривой заданной параметрически.

В декартовой системе координат длина дуги L= . Рассмотрим подынтегральное выражение внесем dx под корень - это выражение называется дифференциалом дуги. L= .

Если кривая L задана параметрически.

= =

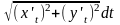
Длина кривой заданной параметрически, выражается через определенный интеграл L= .

Замечание: При вычислении длины кривой заданной параметрически нижний предел интегрирования должен быть меньше верхнего предела интегрирования.

П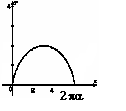 ример: Найти длину 1 арки циклоиды.

Вычислим длину 1 арки циклоиды

0t2

= = = = = = ==

L= = = = =-4(-1-1)=

=8 (ед)

Если кривая L задана в полярной системе координат

= =

= =

=

Длина дуги кривой в полярной системе координат L=

Пример: Вычислить длину кардиоиды . В силу симметричности кривой вычислим ½ длины. Полярный угол ½L= = =

= = = = =

= =

½L= = =4(1-0)=4  L=4*2=8 (ед).

1.22Объем тела через площадь поперечного сечения.

Пусть дано некоторое тело и известно, что площадь поперечного сечения плоскости перпендикулярна оси OX. Разобьем тело на части плоскостями x=x_i перпендикулярными оси OX. Отрезок [a,b], лежащий на оси OX, разобьется соответственно точками x_i на n частей: a=x₀<x₁<x₂<…<x_n=b. x_i = x_i+1 – x_i - длина [x_i ; x_i+1]. В каждой точке x принадлежащей отрезку [a,b] известно поперечное сечение этого тела, то есть площадь поперечного сечения является функцией от x(S(x)). На i отрезке выберем произвольную точку C_i и заменим объем i части тела объемом прямого цилиндра V_i = S_осн  высоту=S(C_i)  x_i ; объем тела приближенно равен сумме объемов прямых цилиндров V_T  ; Причем равенство будет тем точнее, чем больше частей разбиения тела и чем меньше длина отрезка x_i . Переходя к пределу получаем V_T= . Этот предел интегральных сумм является определенным интегралом где S(x) – площадь поперечного сечения.

Объем тела вращения.

Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)0 вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX.

Как известно, объем тела выражается через площадь поперечного сечения по формуле: . В данном случае поперечными сечениями являются круги радиусом R_кр=f(x); S_кр=S(x) = f ²(x)  V_OX= . Если криволинейная трапеция ограниченная линиями вращается вокруг оси OY, то объем полученного тела вращения V_OY=

Замечание: Если фигура не является криволинейной трапецией, то ее нужно разбить на нужные части, либо достроить нужные части и вычислять объем тела вращения, как неполый через сумму или разность объемов частей.

Пример: Вычислить объемы тел вращения, ограниченного линиями y=0; x=0; x=1; y=e^x.