Интегрирование выражений, содержащих квадратный трехчлен.
;
.
Каждый из указанных двух интегралов берется в два приема:
а) выделяется полный квадрат в квадратном трехчлене:
;
б)
заменой
исходный интеграл сводится к табличным
интегралам.
Пример: Найти неопределенный интеграл.
.
Решение:
Выделим сначала полный квадрат из квадратного трехчлена:
.
Затем
проведем замену переменных, положив
и
.
Тогда
Каждый из интегралов вычислим отдельно:
Здесь
мы сделаем замену переменных, положив
(тогда
и
):
Окончательно получим
=
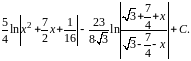
Интегрирование рациональных дробей.
Выражения
вида
,
где а
вещественное, k, l
натуральные числа, а квадратный трехчлен
не имеет действительных корней, назовем
простейшими сомножителями.
Известна
основная теорема алгебры:
любой многочлен
степени n
можно разложить в произведение простейших
сомножителей:
=
(4)
где
число;
Дроби
вида
,
где k,
l
натуральные
числа,
простейший сомножитель, будем называть
простейшими
рациональными дробями.
Используя (4), можно доказать следующую
теорему.
Теорема.
Любая
правильная рациональная дробь
может быть представлена в виде суммы
простейших рациональных дробей (m и
n-степени многочленов, стоящих в числителе
и знаменателе соответственно). Эта сумма
строится следующим образом в два этапа:
1)
каждый простейший множитель вида
порождает следующую сумму из
слагаемых:
;
2)
каждый сомножитель вида
порождает следующую сумму из
слагаемых:
В
результате мы получим следующее
разложение правильной дроби на простейшие:
=
+...+
...+
(5)
Считая в дальнейшем, что коэффициент при старшей степени у многочлена равен единице, на примерах решения задач покажем, как используется сформулированная теорема на практике.
Пример:
Разложить дробь
на простейшие дроби.
Решение:
Разложим знаменатель на простейшие
сомножители:
.
Тогда
;
Две
дроби, имеющие одинаковые знаменатели,
равны, значит равны их числители, то
есть
.
Два
многочлена тождественно равны тогда,
когда у них совпадают коэффициенты при
одинаковых степенях
,
следовательно, можно записать следующую
систему уравнений:
.
Решая
ее, находим, что
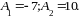
Окончательно
положим
.
Пример:
Разложить дробь
на простейшие дроби.
Решение:
Разложим
знаменатель дроби на простейшие
сомножители:
.
Тогда
или
.
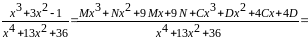
Как и в предыдущей задаче, составим систему уравнений для нахождения неизвестных коэффициентов:
Выражая
из первых двух уравнени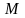й
и
через
и
соответственно и подставляя найденные
значения в последующие два уравнения,
находим:
Отсюда
Следовательно,
Из разложения (5) следует, что интегрирование правильных рациональных дробей сводится к интегрированию простейших дробей.
Пример:
Найти
.
Решение: Поскольку рациональная дробь, стоящая под знаком интеграла, является неправильной, то представим ее в виде суммы многочлена и правильной дроби (для этого достаточно найти частное и остаток от деления числителя на знаменатель).
Тогда
Разложим
дробь
на простейшие дроби:
;
Отсюда
Следовательно,
Но тогда:
