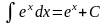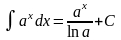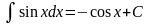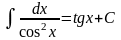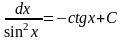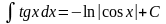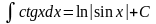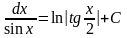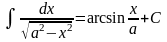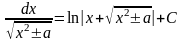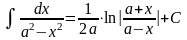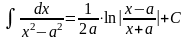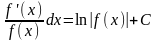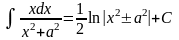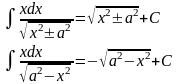- •Волгодонский инженерно-технический институт - филиал нияу мифи
- •Замена переменных в неопределенном интеграле.
- •Интегрирование выражений, содержащих квадратный трехчлен.
- •Интегрирование рациональных дробей.
- •Интегрирование некоторых иррациональных алгебраических функций.
- •Интегрирование тригонометрических выражений.
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал нияу мифи
Конспект лекций
по теме:
«Интегральное исчисление»

Волгодонск
2010
Первообразная и неопределенный интеграл.
Определение:
Первообразной
F(x)
для функции f(x)
на промежутке называют функцию,
производная которой
 .
.
Пример.
Для функции
 :
первообразная
:
первообразная
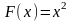 на R,
так как
на R,
так как
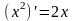 при любом х.
при любом х.
Лемма.
Если
производная функции на промежутке
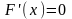 ,
то
,
то
 .
.
Доказательство:
По теореме Лагранжа для любых x1,
x2
выполняется
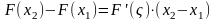 ,
где
,
где
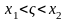 ,
так как
,
так как
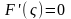
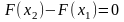
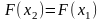 в
силу произвольности точек x1
и x2
F(x)
= C(const).
в
силу произвольности точек x1
и x2
F(x)
= C(const).
Ч.т.д.
Теорема: Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x) F(x)=Ф(x)+С.
Доказательство:
так как
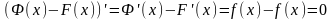
по Лемме
по Лемме
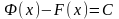
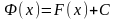 .
.
Ч.т.д.
Таким
образом, из теоремы следует, что выражение
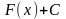 описывает все множество первообразных
функции f(x).
описывает все множество первообразных
функции f(x).
Определение:
Неопределенным
интегралом функции f(x)
по переменной x
называется множество всех её первообразных
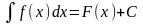 ,
где
.
,
где
.
‒ знак
интеграла, f(x)
– подынтегральная функция, x
– переменная интеграла,
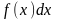 ‒ подынтегральное выражение, С – const
интегрированная.
‒ подынтегральное выражение, С – const
интегрированная.
Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат.
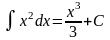 ;
;
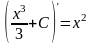 -
верно
-
верно
Свойства неопределенного интеграла.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
Замечание: Условием существования неопределенного интеграла является непрерывность подынтегральной функции.
Замена переменных в неопределенном интеграле.
Пусть
на промежутке T
определена функция
 ,
на множестве значений которой определена
функция
,
на множестве значений которой определена
функция
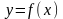
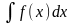 =
=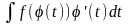 .
Можно выделить два вида с заменой
переменной.
.
Можно выделить два вида с заменой
переменной.
Первый тип.
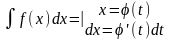 .
.
Такие замены стандартные, их нужно знать.
Пример:
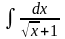 =
=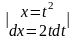 =
=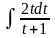 =
=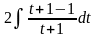 =
=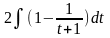 =
=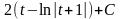 =
=
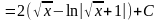 .
.
Второй тип.
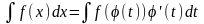 ,
нужно в подынтегральной функции поискать
производную какой-нибудь её части.
,
нужно в подынтегральной функции поискать
производную какой-нибудь её части.
Пример:
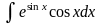 =
=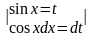 =
=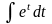 =et+C=esin
x+C.
=et+C=esin
x+C.
Таблица интегралов.
|
От степенных функций |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
|
От показательной функции |
7 |
|
8 |
|
|
От тригонометрических функций |
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
|
для обратных тригонометрических функций |
17 |
|
18 |
|
19 |
|
20 |
|
|
Длинный логарифм |
21 |
|
|
Высокие логарифмы |
22 |
|
|
Полезные интегралы |
23 |
|
24 |
|
25
26 |
|
Интегрирование по частям в неопределенном интеграле.
Т.к.

 .
Проинтегрируем обе части равенства:
.
Проинтегрируем обе части равенства:
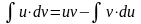 .
.
Интегрирование по частям применяют в случаях:
1. Подынтегральная сумма представляет собой произведение многочлена на показательную функцию или тригонометрическую. За u берется многочлен, за dv ‒ оставшееся.
Пример:
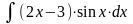 =
= =
=
=
=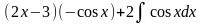 =
=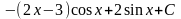 .
.
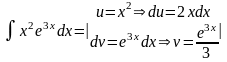 =
=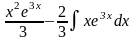 =
=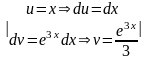 =
=
= =
=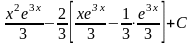 .
.
2. Подынтегральная функция представляет собой произведение многочлена на логарифмическую или обратную тригонометрическую функцию. За часть u нужно взять логарифмическую или обратную тригонометрическую функцию.
Пример:
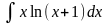 =
=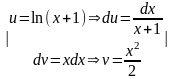 =
=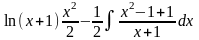 =
=
=
=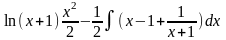 =
=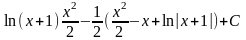 .
.
 =
=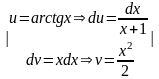 =
= =
=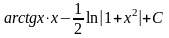 .
.
3. Подынтегральная функция представляет собой произведение тригонометрической на показательную функцию. Неважно что брать за u.
Пример:
I=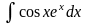 =
=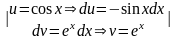 =
=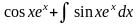 =
=
=
=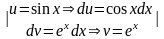 =
=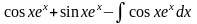 .
.
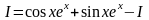 ;
;
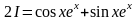 ;
;
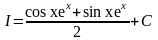 .
.

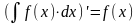
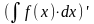

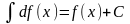

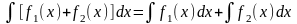
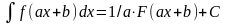
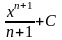 ,
n≠-1
,
n≠-1