18) Теорема взаимности и метод расчёта, основанный на ней

Принцип взаимности основан на теореме взаимности, которую сформулируем без доказательства: для линейной цепи ток  в k – й ветви, вызванной единственной в схеме ЭДС , находящейся в i – й ветви,

будет равен току  в i – й ветви, вызванному ЭДС , численно равной ЭДС , находящейся в  k – й ветви,

.

Отсюда в частности вытекает указанное выше соотношение .

Иными словами, основанный на теореме взаимности принцип взаимности гласит: если ЭДС , действуя в некоторой ветви схемы, не содержащей других источников, вызывает в другой ветви ток  (см. рис. 3,а), то принесенная в эту ветвь ЭДС  вызовет в первой ветви такой же ток  (см. рис. 3,б).

В качестве примера использования данного принципа рассмотрим цепь на рис. 4,а, в которой требуется определить ток , вызываемый источником ЭДС .

Перенесение источника ЭДС  в диагональ моста, где требуется найти ток, трансформирует исходную схему в цепь с последовательно-параллельным соединением на рис. 4,б. В этой цепи

,

(7)

 

где .

В соответствии с принципом взаимности ток  в цепи на рис. 4,а равен току, определяемому соотношением (7).

19) Гармонические колебания , их описание и характеристики

Э лектромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим. Наименьший промежуток времени, по истечении которого наблюдаются повторения мгновенных значений периодиче­ских величин, называется перио­дом. Если величину, являющуюся периодической функцией времени t обозначить через F (t), то для лю­бого положительного или отрицательного значения аргумента t спра­ведливо равенство F(t±T) = F(t), где Т — период.

Геометрически это значит, что ординаты двух произвольных точек графика F(t) с абсциссами, отли­чающимися на Т одинаковы.

Величина, обратная периоду, т. е. число периодов в единицу времени, называется частотой: f=1/T

Частота имеет размерность l/сек, а единицей измерения часто­ты служит герц (гц); частота равна 1 гц, ес­ли период равен 1 сек.

Преобладающим ви­дом периодического процесса в электриче­ских цепях является синусоидальный режим, характеризую­щийся тем, что все на­пряжения и токи явля­ются синусоидальными функциями одинако­вой частоты. Это воз­можно только при за­данных синусоидаль­ных э.д.с. и токах ис­точников. Тем самым обеспечивается наибо­лее выгодный эксплуа­тационный режим ра­боты электрических установок.

Как известно из курса математическо­го анализа, синусоида является простейшей периодической функцией; всякие другие несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид, имеющих кратные. Поэтому для исследования процессов в цепях переменного тока в первую очередь необ­ходимо изучить особенности цепей синусоидального тока. Так как ко­синусоида может рассматриваться как сдвинутая синусоида, то усло­вимся к синусоидальным функциям причислять и косинусоидальные. Колебания, выражаемые этими функциями, будем называть гар­моническими.

На рис. 2-1 изображены функции

, здесь 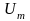— максимальное значение или амплитуда, — скорость изменения аргумента (угла), на­зываемая угловой частотой; она рав­на произведению ча­стоты на 2π: ω=2πf(3), рад/сек; φ—начальная фаза, определяемая величи­ной смещения гармо­нической функции от­носительно начала координат; при запи­си (1) она измеря­ется абсциссой поло­жительного максиму­ма, а при (2) — абсциссой точки пере­хода отрицательной полуволны в положи­тельную.

Начальная фаза φ представляет алгебраическую величину. На рис. 2-1, а и г угол φ отрицателен. На рис. 2-1, б и в угол φ положителен.

За аргумент функций (1) и (2) может быть принято время t или соответственно угол ωt. Аргументу t соответствует период Т, а аргументу ωt — период ωt=2π. Следует иметь в виду, что аргумент ωt измеряется в радианах, причём в тех же единицах измеряется и начальная фаза.

Если угол φ вычисляется в градусах, то аргумент ωt также переводится в градусы(1рад=57,3 градуса); в этом случае период составляет 360°.

Величина ωt+ φ, определяющая стадию изменения функций (1) и (2), называется фазовым углом или фазой. С течением времени фаза возрастает, причем после увеличения фазы на 2π цикл изменения синусоидальной величины повторяется.

Рассмотренные понятия, характеризуют гармонические колебания, являются исходными при изучении электрических процессов в цепях переменного тока.