Элементы аналитической геометрии и векторной алгебры

1.1. Аналитическая геометрия на плоскости. Основные понятия. Прямоугольная система координат. Линии и их уравнения. Прямая, уравнения прямой с заданным угловым коэффициентом, проходящей через одну и две точки. Условия параллельности и перпендикулярности прямых.

1.2. Векторы. Основные понятия. Свойства. Линейные операции над векторами. Разложение вектора по базисным. Скалярное произведение векторов.

1.1. Аналитическая геометрия на плоскости.

Расстояние d между двумя точками А(x₁, y₁) и В(x₂, y₂) на плоскости (рис.1) определяется формулой

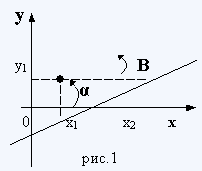
(1)

Угловой коэффициент k =tg  отрезка

АВ равен:

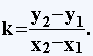(2)

 - угол отрезка с осью абсцисс.

Прямую, заданную угловым коэффициентом k и отрезком b, отсекаемым на оси ординат, можно задать уравнением:

y = kx+b, (3)

а прямую, проходящую через точку (x₁, y₁) - уравнением

y - y₁ = k (x - x₁) (4)

Прямую, проходящую через две точки, задают уравнением

(5)

Общее уравнение прямой имеет вид: Аx + By + C = 0 (6)

Ее угловой коэффициент определяется формулой: (7)

Условия:

а) параллельности прямых: k₁=k₂;

б) перпендикулярности прямых: k₁·k₂= -1.

Если т. M(x,y) делит отрезок A(x₁,y₁) B(x₂,y₂) в отношении λ = AM/MB, то ее координаты определяют по формулам:

;

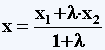Система координат на плоскости.

Расстояние между двумя точками.

Требуется найти расстояние d между точкой А(x₁;y₁) и точкой В(х₂;y₂) в плоскости Oxy/

y

B Искомое расстояние АВ((х₂ – х₁); (y₂ – y₁)), то есть

A

x

Требуется разделить АВ, соединяющий А(x₁;y₁) и В(х₂;y₂) в заданом отношении λ>0, то есть найти координаты точки М отрезка АВ, такой что

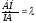
Введем в рассмотрение вектора АМ и МВ. Точка М делит отрезок АВ в отношении λ.

АМ = λМВ (1)

, но АМ((х₂ – х₁); (y₂ – y₁)), то есть АМ=(х – х₁)i+(y – y₁)j и МВ = (х₂ – х)i+ (y₂ – y)j Уравнение (1) принимает вид:

(х – х₁)i+(y – y₁)j = λ (х₂ – х)i+ λ (y₂ – y)j

Учитывая, что равные вектора имеют равные координаты, получим:

х – х₁ = λ (х₂ – х) и y – y₁ = λ (y₂ – y)

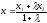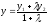(2) (3)

Формулы (2) и (3) называются формулами деления отрезка в данном отношении.

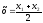
В частности при λ=1 , то есть точка М – середина отрезка АВ.

Замечания:

- если λ=0, то это означает, что А и М совпадают

- если λ<0, то М лежит вне отрезка АВ, говорят что М делит АВ внешним образом.

Площадь треугольника.

Требуется найти S треугольника ABC, с вершинами А(x₁;y₁) B(x₂;y₂) C(x₃;y₃)

y B

A

C

A₁ B₁ C₁ x

Опустим из вершин перпендикуляры на ось Ох. Очевидно, что S_abc=S_aa1bb1+S_b1bc1 – S_a1acc1

Замечание:

- если при вычислении площади получили S=0, то это означает что A,B,C лежат на одной прямой

- если получили S<0, надо брать её модуль

Уравнение прямой на плоскости.

Уравнение прямой с угловым коэффициентом.

Пусть на плоскости Охy задана произвольная прямая, не параллельная оси Оy. Её положение определяется ординатой в точке N(0;b)

y

M(x;y)

y

N(0;b) α x

Из определения тангенса угла следует равенство:, то есть

Введем обозначение tgα = k, получаем уравнение:

y = kx + b (1)

Которому удовлетворяет координаты любой точки М(x;y) прямой.

Число k=tg α называется угловым коффициентом прямой, а уравнение (1) – уравнением прямой с угловым коэффициентом.

- если b=0, следовательно прямая проходит через начало координат

- если y=b, следовательно прямая параллелбна оси Ох (α=0)

- если прямая параллельна оси Oy, следовательно α=90⁰, значит х=а

Общее уравнение прямой.

Рассмотрим уравнение первой степени относительно в общем виде:

Ах+By+c=0 (2)

,где А,В – произвольные числа, причем А и В ≠ 0

Покажем, что уравнение (2) - уравнение прямой линии:

возможны два случая:

1) если В=0 следовательно Ах+С=0, значит 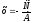- уравнение прямой,параллельной оси Ох и проходящей через точку

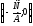
2) если В≠0, следовательно 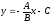- уравнение прямой с угловым коэффициентом k=tgα=-A\C

Итак, уравнение (2) – уравнение прямой линии, оно называется общим уравнением прямой.

Некоторые частные случаи уравнения прямой.

1) если А=0 следовательно прямая параллельна оси Ох

2) если В=0 следовательно прямая параллельна оси Oy

3) если С=0, следовательно Ах+Вy=0, значит прямая проходит через начало координат

Уравнение прямой, проходящей через данную точку в данном направлении.

Пусть прямая проходит через точку М(x₀;y₀) и её направление характеризуется угловым коэффициентом k. Уравнение этой прямой можно записать в виде: y = kx + b, где b – неизвастная величина.

Так как прямая проходит через М(x₀;y₀), то коэффициенты точки удовлетворяют уравнению прямой y₀ = kx₀ + b, отсюда b = y₀ – kx₀

Подставляя значение в уравнение прямой, получим искомое уравнение:

y – y₀ = k(x –x₀) (1)

Уравнение (1) с различными значениями k называются также уравнениями пучка прямых с центром в точке М(x₀;y₀)

Уравнение прямой, проходящей через две точки.

Пусть прямая проходит через точки М₁(x₁;y₁) и М₂(x₂;y₂)

Уравнение прямой, проходящей через точки М₁

y – y₁ = k(x₂ –x₁) (4)

где k – пока неизвестный коэффициент

Так как прямая проходит через точку М₂, то координаты этой точки должны удовлетворять уравнению y₂ – y₁ = k(x₂ –x₁) . Теперь находим k:

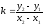
Подставляя k в уравнение (4), получим уравнение прямой, проходящую через точку М₂:

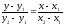(5)

Уравнение прямой в отрезках.

y

M₂(0;b)

b

M₁(a;0) x

0 a

, то есть

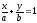(6)

Пусть прямая пересекакт ось Ох в точке M₁(a;0), а ось Оу в точке M₂(0;b). В этом случае уравнение (5) принимает вид (6). Это уравнение называется уравнением прямой в отрезках, так как а и b указывают какие отрезки отсекает прямая на осях координат.

Уравнение прямой, проходящей через данную точку,

перпендикулярно данному вектору.

y

n M(x;y)

M₀(x₀;y₀) x

Найдем уравнение прямой, проходящей через точку M₀(x₀;y₀) перпендикулярно данному ненулевому вектору n(A;B)

Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор М₀М(х-x₀;у-y₀). Поскольку вектора n и М₀М взаимно перпендикулярны, то их скалярное произведение равно 0, то есть

А(х-x₀) + В(у-y₀) = 0 (7)

Уравнение (7) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор n(A;B) перпендикулярный к прямой называется нормальным вектором этой прямой.

Полярная система координат.

у

М(r;φ)

A

r

φ φ

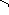
0 x 0 P

Задается точкой 0, называемой полюсом, лучом ОР, называемым полярной осью и единичным вектором е, того же направления что и луч ОР.

Возьмем на плоскости точку М. Положение точки М определяется двумя числами: её расстоянием r от полюса 0 и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки)

Числа r, φ называются полярными координатами точки М. Пишут М(r;φ). При этом r называется полярным радиусом, φ – полярным углом.

Установим связь между прямоугольными и полярными координатами:

Угол между двумя прямыми и условия параллельности

и перпендикулярности двух прямых.

Пусть прямые l₁ и l₂ заданы уравнениями: y = k₁x + b₁ и y = k₂x + b₂

l₂

l₁

φ

α₂ α₁

Требуется найти угол φ, на который надо повернуть в противоположном направлении прямую l_1, вокруг точки их пересечения до совпадения с прямой l₂

Решение:

Имеем α₂ = φ+ α (согласно теореме о внешнем угле) или φ = α₂ - α₁, если φ≠π\2, то tg φ =

= tg(α₂ - α₁)=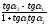 ,но tgα₁ = k₁; tgα₂ = k₂ поэтому:

(10)

Если требуется вычислить острый угол между прямыми, не учитывая какая прямая является первой, а какая второй, то правая часть формулы (10) берется по модулю:

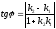
Если прямые параллельны, то tg φ = 0, значит k₁ = k₂

Следовательно, условием перпендикулярности является k₁∙k₂ = -1

Расстояние от точки до прямой.

Пусть заданы прямая L: Ax+By+C=o и точка М₀(х₀;у₀). Требуется найти расстояние от точки М₀ до прямой L.

y

M₁(x₁;y₁) М₀(х₀;у₀)

n(A;B)

0 L x

Решение:

Расстояние от М₀ до Д = │пр_LM₁M0│(где М₁(х₁;у₁) – произвольная точка на прямой L) на направлении нормали n(A;B)

так как точка М₁(х₁;у₁) принадлежит прямой L, то Ах₁+Ву₁+С = 0, следовательно

С = -Ах₁-Ву₁, учитывая это: