24. Определение производной, зависимость между непрерывностью и дифференцируемостью функции

Р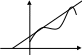 ассмотрим y=y(x) на промежутке x, возьмём т.х Х и придадим точке приращение х>0. Тогда мы получим приращение ф-ии,кот.обознач-ся у=f(x+ х)-f(x). Производной ф-ии у=f(x) наз-ся предел отношения приращения ф-ии к приращению аргумента,при приращении аргумента стремящимся к 0(если предел сущ-т). y’-производная ф-ия, y’= = . если ф-ия в т.х им.конечную производную, то она наз-ся дифференцируемой в т.х. Если ф-ия дифференцируема в каждой точке промежутка Х,то она наз-ся диффер-мой на промежутке. Смысл производной геометрический: знач-е производной f’ ) в т.касания есть угловой коэфиц-т касательной,проведённой к ф-ии y=f(x).

Т.если ф-ия диффер-ма в т. , то она непрерывна в этой точке.

25. Схема вычисления производной, основные правила дифференцирования

Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику функции.

, где  - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: . Ур-е нормали к кривой: .

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1)С = 0, где с-число

2) (u  v) = u  v

3) (uv) = uv + uv

4) , если v  0

5)производн. аргумента x’=1

26.Производная сложной функции. Производная обратных функций.

Пусть y=f(u),a u=g(x). тогда задана сложн.ф-ия y=f(g(x))

Т.если y = f(x); u = g(x) дифференцируемы от своих аргументов, то производная сложн.ф-ии нах-ся по фомуле у’=f’(g(x))*g’(x)

Производная обратных функций.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

, т.к. g(y)  0 , ,

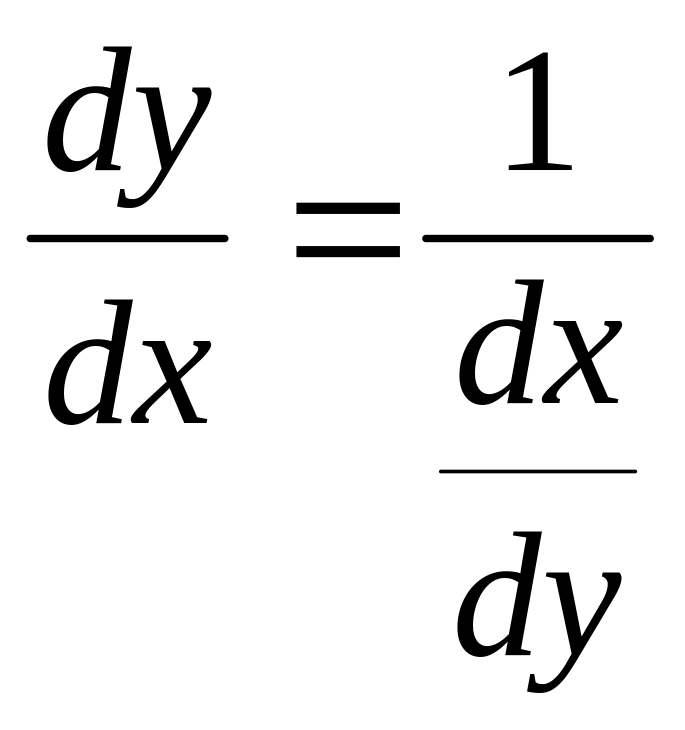
т.е. производная обратной функции обратна по величине производной данной функции.

27. Производные основных элементарных функций, производные высших порядков.

Производная основных элементарных ф-ий: ; ; ;

Производная высших порядков: y=f(x), тогда y’=f’(x), y’’=f’’(x), y’’’=f’’’(x), =( )’

28. Основные теоремы дифференциального исчисления.

Теорема Ферма.

ф-я определена на и в нек-рой точке этого интервала имеет наиб. или наим. значение, тогда если в этой точке определена производная, то она =0, т.е.

Пр. в точке 0 производная =0.

Теорема Ролля.

Пусть на отрезке определена ф-я , причем: непрерывна на , дифференцируема на ,

Тогда сущ-ет точка , что

Теорема Лагранжа.

Пусть на определена ф-я причем:

непрерывна на , диффер. на Тогда сущ-ет точка С, принадлежащ. , такая, что

Теорема Коши.

Пусть и непрерывны на и дифференцируемы на и пусть кроме того , тогда сущ-ет такая, что . Если в кач-ве взять ф-ю. = , то получим т. Лагранжа. Если т. Лагранжа положить , то получим т. Коши.

Теорема Лапиталля-Бернулли.

Пусть и определены и дифф. на содержащим точку за исключением быть может самой точки . Пусть предел при и на , тогда если сущ-ет конечный предел, при то сущ-ет и причем они равны.