20.Бесконечно большие величины

Ф-я наз-тся бесконечно большой при , если  можно найти такое число , что при     .

ББ ф-я при не им.предела. Условно говорят, что и пишут . Св-ва: 1) произведение ББВ на ф-ию, предел кот.не=0,есть ББВ, 2)сумма ББВ и огранич.ф-ии есть ББВ, 3)частное от деления ББВ на ф-ию,имеющую предел есть ББВ.

= (ещё большая бескон-ть)

21. Основные теоремы о пределах ф-ии.

1) Ф-я не может им.более 1-го предела, 2)предел суммы конечного числа ф-ий равен сумме пределов этих ф-ий , 3)предел произведения конечного числа ф-ий равен произведению их пределов

Если кроме того , то сущ-ет предел частного причем предел частного равен частному пределов.

Следствие 1. Постоянный множитель можно выносить за знак предела, т.е.

Следствие 2. Если , то

4)предел частного двух ф-ий=частному их пределов при ус-ии, что предел знаменателя не=0. , 5) если предел ф-ии , , , 6) если некоторые окрест-ти , f(x)< , то их пределы будут связаны знаком .

Признаки сущ-я пределов: 1) если числов.послед-ть монотонна и ограничена, то она им.предел, 2) если в некот.окрест-ти т. ф-ия f(x) заключена между 2мя ф-ми и , т.е , причём и им.одинак.предел А при х , значит ф-ия f(x)им. Тот же предел А.

1-метод раскрытия неопределенности-сокращение общего множителя.

2-метод: деление на степень .

разделим на

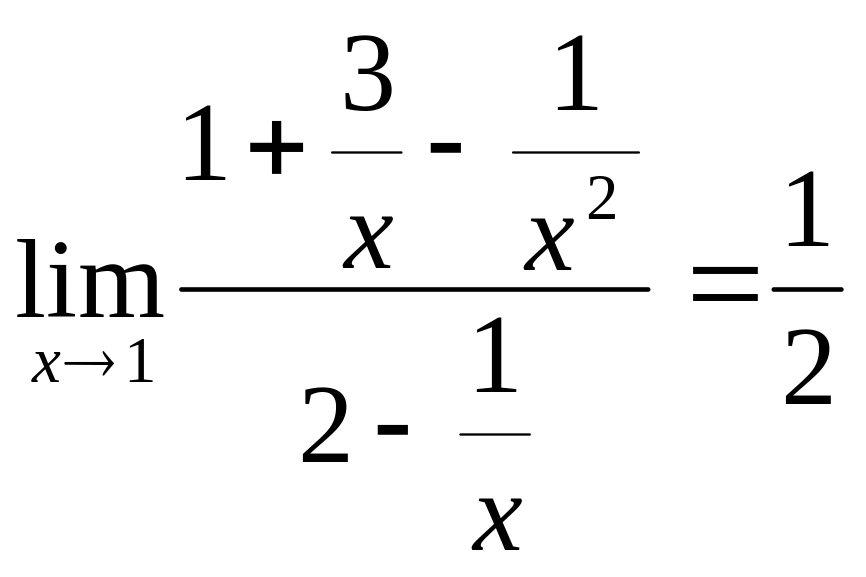
22. Замечательные пределы.

Первый замечательный предел.

_{Пример:}

Второй замечательный предел.

_{следствие:}

23. Понятие непрерывности ф-и.

Ф. , определенная на наз-ся непрерывной в точке если 1) , 2) сущ-т предел , 3) ф-ия в точке определена . т.е. сущ-т т. .

Ф-ия наз-ся непрерывной в т. ,если она определена в этой точке и бесконечно малому приращению аргумента соот-т бесконечно малое приращение ф-ии. Т. наз-ся точкой разрыва ф-ии, если в этой точке ф-ия не явл-ся непрерывной. Различают точки разрыва 1го рода (когда сущ-т конечные односторонние пределы ф-ии слева и справа не = друг другу) и 2го рода (когда хотя бы один из односторонних пределов слева или справа = или не сущ-т). Точка в разрыве 1го рода также относ-ся к точке устранимого разрыва, когда lim ф-ии в точке сущ-т, но не = знач-ю ф-ии в этой точке.

Св-ва ф-ий непрерывности в точке( непрерывна в точке только тогда, когда ):1)Если и непрерывны в точке ,то непрерывна в этой точке их сумма, разность, произведение, а также частное при усл. _{, 2) если y=f(x) непрерывна в точке x0 и f(x0)>0, то сущ-т такая окрестность в т.х0, в которой f(x)>0, 3)если ф-ия y=f(u) непрерывна в точке u0, а ф-ия u=} непрерывна в точке х0, причём u0= , тогда ф-ия y=f( ) непрерывна в точке х0.

Св-ва непрерывных ф-ий на отрезке: 1)т.Бальцама - Коши: Пусть ф. непрерывна на отрезке и на концах отрезка имеет значение разных знаков, тогда сущ-ет точка такая, что

Т еорема.Пусть ф. непрерывна на отрезке причем . Пусть –число, заключенное между А и В, тогда сущ-ет точка такая, что _,

2) т. Вейерштрасса: Если ф. определена и непрерывна на , то она ограничена на этом отрезке.

3) т. Вейерштрасса: Если непрерывна на , то она достигает на этом отрезке своего наиб. и наим. значения.