3.Обратная матрица.
А-1 наз-ся обратной,если А* А-1= А-1*А=Е.(для кв.матрицы А)
Если
кв.матрица А им.обратную,то А-1
также б.кв того же порядка. Для сущ-я
обратн.матрицы нужно чтобы определитель
А не=0,такая матрица А наз-ся невырожденной
или несобственной. 
-вырожденная.
Теорема.обратная матрица А-1 сущ. И единственна тогда и только тогда,когда матрица А невырожденна. Доказат-во: пусть сущ. А-1,тогда по определению получ-м А* А-1= А-1*А=Е
=
,
следовательно 
.
Докажем обратное утвержд-е. пусть 
.
Рассмотрим кв.матрицу n-го
порядка (
),называемую
присоединённой или взаимной,эл-ми
которой явл.алгебраические дополнения
матрицы А транспонированной 
=
,
i=
j=
B=
=
= 
A* =
А-1=
*
,
где
Правило
вычисления обратн.матрицы: 1)наход.
определитель матрицы А,если
,то
обратн. не сущ-т, если 
находим
алгебраическ.дополн.всех эл-ов матрицы
и составляем из них присоедин матрицу
=
,
3) А-1=
*
,
4)проверка А* А-1=
А-1*А=Е
4 Ранг матрицы.
Рангом матрицы А наз-ся наивысший порядок,отличный от нуля миноров этой матрицы .обознач-ся r(A). Св-ва ранга:1)ранг матрицы не превосходит меньший из её размеров, 2)ранг=0,тогда и только тогда,когда все эл-ты матрицы=0, 3)для кв.матрицы порядка n ранг А=n тогда и только тогда,когда матрица невырождена.
Теорема.Ранг
матрицы не меняется при эл-ных
перобразованиях матрицы. Матрица наз-ся
ступенчатой если выпол-ся след.ус-ия:1)i-ая
строка нулевая, то i+1ая
строка тоже будет нулевой, 2)если в iой
и iой+1ой
строках,первые не нулевые эл-ты стоят
в столбцах с номерами k
и l,
то k
l.
Ранг ступенчатой матрицы=числе ненулевых
строк. Св-ва ранга:1)r(A+B)
r(A)+r(B),
2)r(A+B)
r(A)-r(B)
,
3)r(A*B)
min
,
4)r(
)=r(A),5)r(A*B)=r(A),если
В-кв.матрица с определителем не=0,
6)r(A*B)=r(A)+r(B)-n,где
n-число
столбцов А или число строк В
5.Системы линейных уравнений.
Совокупность ур-ний вида
(1) - с-ма
–линейных ур-ний с
–неизвестным
Числа
наз-тся коэффициентами с-мы. Числа
- свободными коэф-ми.
Решением
с-мы (1) наз-тся совокупность чисел
при подстановке к-рых в с-му (1) вместо
получаем верные числовые рав-ва.
Решить с-му, значит найти все ее решения, либо доказать, что их нет.С-ма наз-тся совместной, если она имеет хотя бы одно решение, несовместной- если решений нет. Матрица составлена из коэф-тов
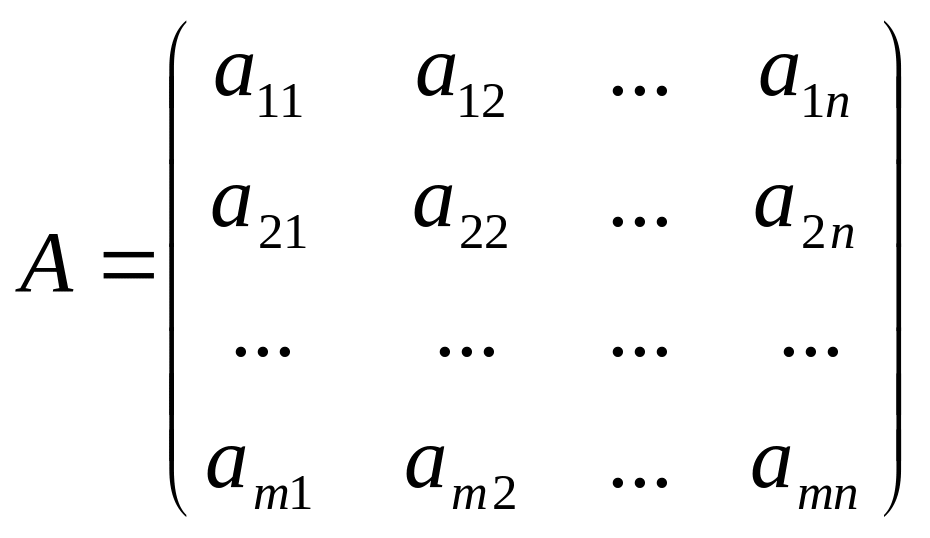наз-тся матрицей
с-мы (1).
Х=
-столбец
неизвестных, В=
-столбец
свободных членов.
АХ=В.
Пусть число ур-ий в системе=числу
неизвестных,тогда матрица системы А
будет квадратной, а её определитель
будем наз-ть определителем системы.
Предроложим,что матрица А невырождена.тогда
сущ.обратная матрица 
.
Умножим матричное ур-ие АХ=В на матрицу
:
*АХ=В*
,
ЕХ=
В,
Х=
В(матричный
м-д)
М-д Гаусса: применяется для произвольной с-мы линейных ур-ний.
С-му
будем наз-ть ступенчатой, если матрица
имеет ступенчатый вид. При решении с-м
линейных ур-ний нам понадобится след
алгоритм: 1)Запишем расшир. матрицу и
приведем ее к ступенчатому виду,2)если
ранги не равны, то с-ма несовместна,
3)если ранги равны и равны числу
,
то с-ма совместна и остается записать
ее решение, 4)используя ступенчатый вид
расширенной матрицы запишем соотв.
ступенчатую с-му., 5)если
=
,
т.е. ранг совпадает с числом неизвестных,
то с-ма имеет единственное решение.
Двигаясь снизу
вверх выражаем каждую из неизвестных.
1)если , то в с-ме ур-ний и неизвестных. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.
Пример. Решить систему линейных уравнений методом Гаусса.
Составим
расширенную матрицу системы.
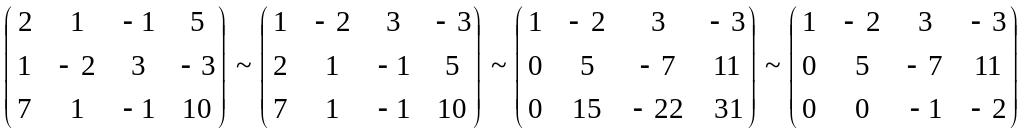исходная
система может быть представлена в виде:
,
откуда получаем: x3
= 2; x2
= 5; x1
= 1.
Правила Крамера:
С-ма линейных ур-ний наз-тся крамеровской, если число ур-ний совпадает с числом неизвестных и определитель матрицы с-мы отличен от 0.
Т. Крамеровская с-ма имеет единственное решение, к-рое находится по ф-лам
,
где -определитель
матрицы с-мы, а
-
определитель,полученный из
подстановкой вместо
того
столбца столбец свободных коэф-тов.
Пр.
;
;
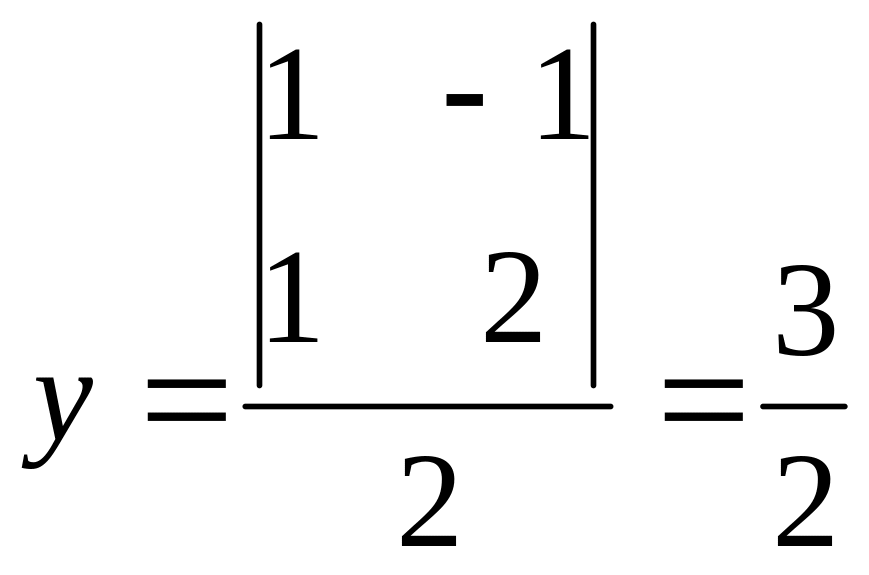;ответ:
Матричный метод решения с-мы линейных ур-ний.
Этот
метод основан на рав-ве
.
Пр.
;
;
