37. Первообразная функция. Неопределенный интеграл.
Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:F(x) = f(x).
первообразных для одной и той же функции м.б. бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.F1(x) = F2(x) + C.
Неопределенный интеграл. Неопред.интегралом ф-ии f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают:
Ус-ем сущ-я неопред.интеграла на некотором отрезке явл-ся непрерывность ф-ии на этом отрезке.
Св-ва:
1.)
2.)
3)
4.
)
где u,
v,
w
– некоторые функции от х, 5)
Таблица неопред.интегр.:
=
=
=
=ln
=
=
ex
+ C
=
sinx + C
=
-cosx + C
=
tgx + C
=
-ctgx + C
=
arcsin
+ C
=
38. Неопределенный интеграл и его св-ва.
Неопред.интегралом ф-ии f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают:
Ус-ем сущ-я неопред.интеграла на некотором отрезке явл-ся непрерывность ф-ии на этом отрезке.
Св-ва: 1.) 2.) 3)
4.) где u, v, w – некоторые функции от х. 5)
Таблица неопред.интегр.:
=
=
=
=ln
=
= ex + C
= sinx + C
= -cosx + C
= tgx + C
= -ctgx + C
= arcsin + C
=
39. Интегралы от основных элементарных функций
значения неопределенных интегралов большинства элементарных ф-ий: =
=
=
=ln
=
= ex + C
= sinx + C
= -cosx + C
= tgx + C
= -ctgx + C
= arcsin + C
=
40. метод замены переменных.
Если
требуется найти интеграл
,
но сложно отыскать первообразную, то
с помощью замены x
= (t)
и dx
= (t)dt
получается:
Пример.
Найти неопределенный интеграл
.
Сделаем замену t = sinx, dt = cosxdt.
41. Интегрирование по частям.
Способ основан на формуле производной произведения:(uv) = uv + vu, где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав,
получаем:
,
Формула
интегрир-я по частям:
или
Пример.
42. Определенный интеграл.
Определенным
интегралом от ф-и
на
наз-тся
конечный предел её интегральной суммы,
когда число элемент. отрезков неограниченно
возрастает, а длина наиб. из них стремится
к нулю. Обозначается:
Число a называется нижним пределом интегрирования, b- верхним пределом интегрирования, f(x)- подинтегральной ф-ей, х-переменной интегрирования.
По определению
(1)
след-но величина определенного интеграла не зависит от переменной интегрирования, т.е.
Ф-я, для к-рой существует предел (1) наз-тся интегрированием на .
Геом. смысл определенного интеграла состоит в том, что =S криволин. трапеции, ограниченной сверху графиком ф-и (f(x)≥0), снизу осью Ох, слева и справа- прямыми х=а и х=в.
43. Св-ва опред. интеграла:
1)
2)при перестановке пределов интегрирования, знак определенного интеграла меняется на противоположный
3)если
и
интегрируемы
на
ф-и, тогда
±
также
интегрируемы. Причем
4)св-во
аддитивности. Пусть
разбит на
элементарных отрезков след. образом
,
тогда
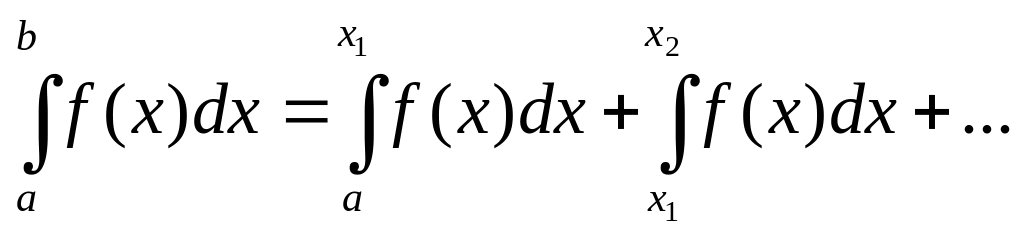
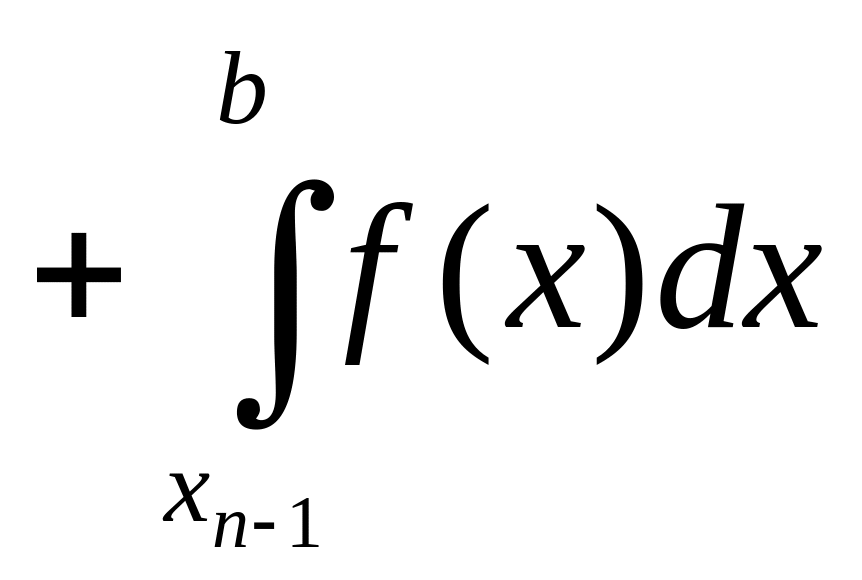
5)постоянный множитель можно выносить за знак определенного интеграла.
6)если
интегрируема
на
(a<b),
причем f(x)≥0,
тогда
7)пусть
ф-и f(x)
и g(x)
интегрируемы на
(a<b)
и на всем отрезке f(x)
≤
g(x).
Тогда
8)пусть
ф-я f(x)
интегрируема на
(a<b),
тогда
также интегрируема на
,
причем
Т.
(об оценке опред. интеграла). Если ф-я
интегрируема
на
(a<b)
и для всех
вып-тся нерав-во
,
тогда
Т.
(о среднем значении) Если ф-я
непрерывна на
,
то на этом отрезке существует точка с,
такая что
44.
ф-ла Ньютона-Лейбница.
Если функция F(x)
– какая- либо первообразная от непрерывной
функции f(x),
то
это выражение известно под названием формулы Ньютона – Лейбница.
Доказ-во:
Пусть F(x)
– первообразная функции f(x).
Тогда в соответствии с приведенной
выше теоремой, функция
- первообразная функция от f(x).
Но т.к. функция может им.бесконечно
много первообразных, кот. будут отличаться
друг от друга только на какое – то
постоянное число С, то
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
Тогда
.
А
при х = b:
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Теорема доказана.
Иногда
применяют обозначение F(b)
– F(a)
= F(x)
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.